Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические основы анализа переходных процессовСодержание книги
Поиск на нашем сайте
Алгоритм расчета переходного процесса классическим методом Для анализа переходного процесса предварительно следует привести схему к минимальному числу накопителей энергии, исключив параллельные и последовательные соединения однотипных реактивных элементов (индуктивностей или емкостей). Система интегродифференциальных уравнений, составленных в соответствии с законами Кирхгофа или методом контурных токов, может быть сведена путем подстановки к одному дифференциальному уравнению, которое используется для составления характеристического уравнения. Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования. Поэтому для решения уравнений порядка выше второго применяют другие методы, в частности операторный метод, основанный на применении преобразования Лапласа и исключающий трудоемкую процедуру отыскания постоянных интегрирования. Для практических целей при анализе переходных процессов в любой схеме классическим методом может быть рекомендован следующий алгоритм. 1. Рассчитать принужденный (установившийся) режим при t→∞. Определить принужденные токи и напряжения. 2. Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями. 3. Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. Существуют приемы, упрощающие операцию отыскания корней характеристического уравнения, например, приравнивание нулю входного операторного сопротивления цепи, которое получается путем замены в выражении комплексного сопротивления цепи множителя "jω" на оператор "р". 4. Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения. 5. Переписать величины, полученные в п. 4, и производные от них при t = 0. 6. Определить необходимые зависимые начальные условия, используя независимые начальные условия. 7. Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования. 8. Записать законы изменения искомых токов и напряжений. Переходные процессы в электрических цепях с последовательно соединенными резисторами и катушками В данном разделе предполагается не только практическое знакомство с классическим методом расчета переходных процессов, но и с особенностями самих процессов в рассматриваемых задачах. Включение цепи с резистором и катушкой на синусоидальное напряжение
Если напряжение источника цепи (рис. 5.6) u = Umsin(ωt + ψ), то установившийся ток iу = Um / Z sin(ωt + ψ - φ), где: Свободный ток определяется iсв = A e-t/τ. Суммируя установившуюся и свободную составляющие, получим выражение для переходного тока: i = iу + iсв = Um / Z sin(ωt + ψ - φ) + A e-t/τ.
используя независимые начальные условия при t = 0 i(0-) = i(0+) = 0, находим постоянную интегрирования: A = -Um / Z sin(ψ - φ). Тогда переходный ток:
Зависимости переходного тока от времени при различных значениях разностей ψ - φ показаны на рис. 5.7. Их анализ позволяет сделать следующие выводы. 1. Если в момент включения установившийся ток равен нулю (ψ - φ = 0 или ψ - φ = π), то свободной составляющей тока не возникает и в цепи сразу возникает установившийся режим: i = iу = Im sin(ωt) = Um / Z sin(ωt). 2. Если в момент включения установившийся ток имеет наибольшее значение (ψ - φ = π / 2), свободный ток достигает максимального по модулю значения приблизительно через половину периода, однако ни при каких условиях он не может превышать удвоенной амплитуды установившегося тока (рис. 5.7 б). Апериодический процесс Между разрядом конденсатора на резистор с катушкой и включением на постоянное напряжение контура (см. рис. 5.16) существует аналогия. Так же, как при разряде конденсатора, установившаяся составляющая тока равна нулю. Установившееся напряжение на конденсаторе uCу = U. Следовательно, начальное значение свободной составляющей напряжения на конденсаторе
uCсв(0+) = uC(0+) - uCу(0-) равно uCсв(0+) = -U. То есть знаки постоянных интегрирования А1 и А2 в отличие от рассмотренного в п. 5.6 случая изменяются на противоположные. В этом случае переходное напряжение на конденсаторе, ток и напряжение на катушке определяются по формулам:
Кривые uC(t), uL(t) и i(t) приведены на рис. 5.17. Колебательный процесс Включение рассматриваемого контура на постоянное напряжение может сопровождаться колебательным переходным процессом. При этом в отличие от процесса разряда конденсатора (см. п. 5.6) знак начального значения преходящего напряжения, следовательно, и коэффициента А, изменится на противоположный. Переходные напряжения и ток приобретут вид:
Кривые uC(t) и i(t) показаны на рис. 5.18. Кривая тока отображает затухающие колебания относительно нулевого значения, а напряжения на конденсаторе – относительно установившегося значения. Следует отметить, что за время переходного процесса контура часть энергии источника переходит в тепло, а другая часть запасается в электрическом поле конденсатора в виде:
Математические основы анализа переходных процессов Задача исследования переходных процессов заключается в том, чтобы выяснить, по какому закону и как долго будет наблюдаться заметное отклонение токов в ветвях и напряжений на участках цепи от их установившихся значений. Так, например, если в исследуемой ветви некоторой цепи до коммутации существовал постоянный ток I1, а в установившемся режиме после коммутации он стал I2, то нас будет интересовать закон изменения переходного тока i между моментом коммутации (t=0) и тем неизвестным нам моментом времени t1, когда переходный процесс можно считать закончившимся. При анализе переходных процессов в электрических цепях считается, что: 1. рубильники включаются и размыкаются мгновенно, без возникновения электрической дуги; 2. время переходного процесса, теоретически бесконечно длительное, (переходный режим асимптотически приближается к новому установившемуся режиму), ограничивают условным пределом – длительностью переходного процесса; 3. установившийся режим после коммутации рассчитывают при теоретическом условии t→∞, т.е. когда после коммутации прошло бесконечно большое время. Установившийся режим до коммутации рассчитывают обычно в предположении, что к моменту коммутации в цепи закончился предыдущий переходный процесс. Хотя иногда приходится анализировать переходные процессы, возникающие в цепи, когда предыдущий переходный процесс, вызванный прежними коммутациями, еще не закончился. Но это не изменяет теоретическую постановку задачи. Анализ переходных процессов производят путем решения дифференциальных уравнений, составленных для исследуемой электрической цепи на основе законов Кирхгофа или метода контурных токов.
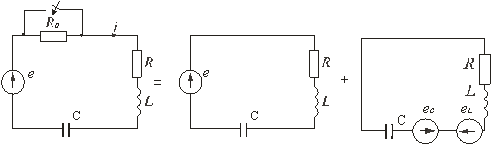
Рис. 5.1 Пусть в некоторой цепи (рис. 5.1 а) внезапно изменяется сопротивление. До коммутации в цепи существовали сопротивления R0 и R, после коммутации остается только R. Требуется определить переходный ток i. Электрическое состояние схемы после коммутации описывается интегродифференциальным уравнением, записанным на основании II закона Кирхгофа для мгновенных значений токов и напряжений: (5.1)
Если это уравнение продифференцировать по времени получим линейное дифференциальное уравнение второго порядка, у которого в качестве постоянных коэффициентов выступают параметры цепи или их комбинации: (5.2)
Из математики известно, что полное решение линейного дифференциального уравнения с постоянными коэффициентами находят в виде суммы частного решения неоднородного и общего решения соответствующего однородного уравнения. Поскольку в правой части дифференциальных уравнений, описывающих электрическое состояние цепей, обычно находится напряжение (или ток) источника (внешняя вынуждающая сила), то частное решение находят из анализа установившегося режима после коммутации. Отсюда этот режим называют принужденным и соответственно токи или напряжения, найденные в данном режиме, называют принужденными. Расчет принужденного режима, когда внешние источники вырабатывают постоянную или синусоидальную э.д.с. (ток), не представляет трудностей и может быть осуществлен любым известным методом. Однородное дифференциальное уравнение получают из выражения (5.2) путем "освобождения" его от правой части. Физически это означает, что исследуемая цепь "освобождается" от внешней вынуждающей силы. Токи или напряжения, найденные при решении однородного дифференциального уравнения, называются свободными. Свободные токи и напряжения являются результатом действия внутренних источников схемы: э.д.с. самоиндукции, возникающих в катушках, и напряжений на конденсаторах, когда и те, и другие не уравновешены внешними источниками. Схематически анализ переходного процесса может быть представлен как результат наложения двух режимов: принужденного и свободного. Схема на рис. 5.1 б должна быть рассчитана в установившемся (принужденном) режиме, а схема на рис. 5.1 в — в режиме, когда цепь освобождена от внешних источников. Действительный (переходный) ток в соответствии с принципом суперпозиции равен сумме установившегося (принужденного) и свободного токов: i = iу + iсв. Заметим, что физически существует только переходные токи и напряжения, а разложение их на свободные и принужденные составляющие является математическим приемом, позволяющим упростить расчет переходных процессов в линейных цепях. Напомним, что принцип суперпозиции применим лишь к линейным цепям. Существуют различные методы решения однородного дифференциального уравнения, полученного из выражения (5.2): (5.3)
Классический метод анализа переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений. Решение находят в виде суммы экспонент: (5.4) iсв = A1 · ep1t + A2 · ep2t, где число слагаемых равно порядку дифференциального уравнения. После подстановки экспонент Ak · epkt в исходное уравнение (5.3) и дифференцирования можно получить характеристическое уравнение, из которого определяют корни p1, p2. Если встречаются кратные корни (например, p1 = p2 = P), решение имеет вид A1 · ePt + A2 · ePt. Постоянные интегрирования A1, A2 находят из начальных условий, которые определяют с помощью законов коммутации. Различают независимые и зависимые (после коммутационные) начальные условия. К первым относят значения токов через индуктивности и значения напряжений на емкостях, известные из до коммутационного режима работы цепи. Значения остальных токов и напряжений при t = 0 в после коммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа для схемы после коммутации, называют зависимыми начальными значениями. Классический метод анализа применяют обычно для анализа процессов в несложных электрических цепях.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.108 (0.008 с.) |


 – полное сопротивление цепи;
– полное сопротивление цепи;
 .
.
 ;
; ;
;  .
.
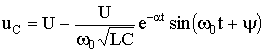 ;
; ;
; .
.
 .
.