
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апериодический разряд конденсатора на катушку и резисторСодержание книги
Поиск на нашем сайте Рассмотрим процесс разряда конденсатора на резистор R и катушку L. Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию uC = uCсв = A1 · ep1t + A2 · ep2t, где А1 и А2 – постоянные интегрирования, определяемые из начальных, условий. Свободный ток равен
Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Поэтому их переходные значения равны свободным составляющим: uC = uCсв; i = iсв. Определим из начальных условий постоянные интегрирования А1 и А2. При t = 0, uC(0) = U0 и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем U0 = A1 + A2; 0 = A1 p1 + A2 p2. Отсюда A1 = U0 p2 / (p2 - p1); A2 = -U0 p1 / (p2 - p1); С учетом начальных условий запишем
Произведение корней по теореме Виета: p1 p2 = 1 / (LC), следовательно, ток
Напряжение на катушке
Графики зависимости тока и напряжения от времени, показанные на рис. 5.14 позволяют говорить об апериодическом разряде конденсатора. Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т.е. функция uC(t) - убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Сделаем некоторые выводы. 1. Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения. 2. При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение. 3. Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля. Предельный апериодический разряд конденсатора на катушку и резистор При соотношении параметров контура из конденсатора, катушки и резистора
где RКР - критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные: p1 = p2 = p = -R / (2L). Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходный ток и переходное напряжение в этом случае имеют вид: uC = (A1 + A2 t) ept;
При начальных условиях uC(0) = U0; i(0) = 0 находим: А1 = U0; A2 = -p U0. С учетом найденных постоянных интегрирования получаем решения: uC = U0 (1 - pt) ept; Зависимости i, uC, uL такие же, как для апериодического разряда. Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой При соотношении параметров контура из конденсатора, катушки и резистора p1,2 = -α ± jω, где α = R / (2L) – коэффициент затухания свободной составляющей; Поскольку
Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1) uCсв = A e-αt sin(ω0t + ψ), Для свободной составляющей тока iсв = C A e-αt (-α sin(ω0t + ψ) + ω0 cos(ω0t + ψ)). С учетом начальных условий при t = 0, uC = U0, i = 0 из последних двух уравнений находим константы интегрирования: U0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cos ψ). и далее
Запишем переходные напряжения и ток: uC = UCm e-αt sin(ω0t + ψ); где
Зависимости переходных напряжения и тока uC, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т0, например:
Часто пользуются логарифмическим декрементом колебания:
В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 или
или  , то корни характеристического уравнения контура вещественные, различные, т.е. р1 ≠ р2, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением
, то корни характеристического уравнения контура вещественные, различные, т.е. р1 ≠ р2, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением .
. ;
;  .
.
 .
. .
. ,
, .
. ;
; .
. , где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:
, где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные: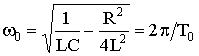 – угловая частота собственных колебаний контура;
– угловая частота собственных колебаний контура; , то можно ввести обозначения
, то можно ввести обозначения ,
,  ,
,  .
. имеем
имеем .
. ;
;  .
.
 .
. .
. , а частота незатухающих колебаний
, а частота незатухающих колебаний 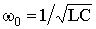 .
.


