
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные цепи с распределенными параметрами. Длинные линии.Содержание книги
Поиск на нашем сайте Линейные цепи с распределенными параметрами. Длинные линии. Электрические цепи можно подразделить на две большие группы: Цепи с сосредоточенными параметрами – здесь привычные параметры сопротивления, индуктивности и емкости сосредоточены в локальных точках цепи 2) цепи с распределенными параметрами- здесь привычные параметры сопротивления, индуктивности и емкости не сосредоточены в локальных точках цепи, а распределены по ее объему. В таких цепях не применимы непосредственно законы Кирхгофа для токов и напряжений, а следует использовать законы электромагнитного поля (уравнения Максвелла). Для оценки, к какому типу отнести цепь с сосредоточенными или распределенными параметрами – следует сравнить ее геометрические размеры с длиной электромагнитной волны λ=V▪T=V/f. Если размеры цепи сопоставимы с l>0,1……0,25∙ λ, то цепь следует рассматривать как цепь с распределенными параметрами, так как здесь нельзя пренебречь временем распространения электромагнитного колебания (волны) по цепи. Если только длина цепи сопоставима с четвертью длины волны, а остальные параметры не сопоставимы, то такую цепь называют длинной линией. Например, для ƒ=5OΓц, т.е. при Т=0.02c и V=3▪108м/c, λ = 6000▪103м и λ/4=1500 км. Для ƒ=108Гц λ/4=0,75м, т.е. уже при l=0,5м к цепи следует подходить как к цепи с распределенными параметрами, так как здесь нельзя пренебречь временем распространения волны. Длинная линия (линия передачи) – устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии в заданном направлении. Линия называется регулярной, если в продольном направлении неизменны ее поперечное сечение, положение ее в пространстве и электромагнитные свойства заполняющих ее сред. Линия является однородной, если в произвольном поперечном сечении параметры среды неизменны. Для исследования процессов в цепи с распределенными параметрами (в основном длинных линий) введем дополнительное условие о равномерности распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости и проводимости. Такую линию называют однородной. Линию с неравномерным распределением параметров часто можно разбить на однородные участки. Уравнения однородной линии в стационарном режиме Под первичными параметрами линии будем понимать сопротивление R0 (Ом/м) индуктивность L0 (Гн/м), проводимость G0 (go) (Cм/м) и емкость C0 (Ф/м), отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины dх << λ/4 со структурой, показанной на рис. 1, где переменная х показывает расстояние от начала линии. Здесь уже можно применить законы Кирхгофа. Пусть напряжение и ток в начале такого элементарного участка равны u и i, а в Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа с учетом, что ток и напряжение следует рассматривать функциями двух переменных координаты х и времени t получим
или после сокращения на dx
Эти уравнения называют телеграфными, так как были рассмотрены при исследовании передачи телеграфных сообщений. Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при ƒ=0 можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока. При гармоническом воздействии, вводя комплексные величины и заменяя ∂⁄∂t на jω, на основании (1) и (2) получаем
Где Ζ o = Ro+jωLo и Y o=Go+jωCo - соответственно комплексные продольное сопротивление и поперечная проводимость схемы замещения на единицу длины линии. Продифференцировав (3) по х и подставив выражение d I ⁄dx из (4), запишем d² U ⁄dx² = Ζ o∙ Y o∙ U Откуда p=± Откуда
И с учетом (9)
В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:
где в соответствии с (5) Откуда КПД линии
И ослабление
Как указывалось при рассмотрении четырехполюсников, единицей ослабления является непер, соответствующий затуханию по мощности в Принято использовать 10 часть, то есть децибелы Линия без искажений Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для его гармонических составляющих ослабление и фазовая скорость различны, т.е. если последние являются функциями частоты. Таким образом, для отсутствия искажений, что очень важно, например, в линиях передачи информации, необходимо, чтобы все гармоники распространялись с одинаковой скоростью и одинаковым ослаблением, поскольку только в этом случае, сложившись, они образуют в конце линии сигнал, подобный входному. Идеальным в этом случае является так называемая линия без потерь, у которой сопротивление R0 и проводимость G0 равны нулю. И фазовой скорости
Из (1) и (2) вытекает, что для получения
И ослабление
Следует отметить, что у реальных линий (и воздушных, и кабельных) Тогда из (5) и (6) получаем
Откуда
Подставив найденные выражения
Уравнения (7) и (8) позволяют определить ток и напряжение в любой точке линии по их известным значениям в начале линии. Обычно в практических задачах бывают заданы напряжение
Обозначив
Откуда
После подстановки найденных выражений
Координату Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения. На основании (13) и (14)
и
Откуда
Выражения (15) и (16) на основании данных эксперимента позволяют определить вторичные параметры Линия без потерь Линией без потерь называется линия, у которой первичные параметры
откуда Раскроем гиперболические функции от комплексного аргумента
Тогда для линии без потерь, т.е. при Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении Как было показано выше, решение уравнений длинной линии можно представить в виде суммы прямой и обратной волн. В результате их наложения в цепях с распределенными параметрами возникают смешанные в том числе и стоячие волны. Поскольку в узлах мощность тождественно равна нулю, стоячие волны в передаче энергии вдоль линии не участвуют. Ее передают только бегущие волны. Чем сильнее нагрузка отличается от согласованной, тем сильнее выражены обратные и, следовательно, стоячие волны. В рассмотренных предельных случаях ХХ и КЗ имеют место только стоячие волны, и мощность на нагрузке равна нулю. Поскольку в узлах мощность тождественно равна нулю, стоячие волны в передаче энергии вдоль линии не участвуют. Ее передают только бегущие волны. Чем сильнее нагрузка отличается от согласованной, тем сильнее выражены обратные и, следовательно, стоячие волны. В рассмотренных предельных случаях ХХ и КЗ имеют место только стоячие волны, и мощность на нагрузке равна нулю Эти уравнения описывают падающие волны, распространяющиеся в линии слева направо. В линии без потерь при согласованном включении существуют только падающие (бегущие) волны. Данный режим работы еще называют режимом бегущей волны.
Иногда на практике используют коэффициент стоячей волны (КСВ).
Область изменения данных коэффициентов:
Если КБВ = 0, КСВ = ¥ – стоячая волна, если КБВ = 1, КСВ = 1 – бегущая волна. Ранее было показано, что
Следовательно:
Переходные процессы в цепях с распределенными параметрами имеют характер блуждающих волн, распространяющихся по цепи в различных направлениях. Эти волны могут претерпевать многократные отражения от стыков различных линий, от узловых точек включения нагрузки и т.д. В результате наложения этих волн картина процессов в цепи может оказаться достаточно сложной. При этом могут возникнуть сверхтоки и перенапряжения, опасные для оборудования. Переходные процессы в цепях с распределенными параметрами возникают при различных изменениях режимов их работы: включении-отключении нагрузки, источников энергии, подключении новых участков линии и т.д. Причиной переходных процессов в длинных линиях могут служить грозовые разряды. Как указывалось, переходный процесс в цепях с распределенными параметрами характеризуется наложением многократно отраженных волн. Рассмотрим многократные отражения для двух наиболее характерных случаев: подключение источника постоянного напряжения к разомкнутой и короткозамкнутой линии. Линейные цепи с распределенными параметрами. Длинные линии. Электрические цепи можно подразделить на две большие группы:
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 968; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.01 с.) |

 конце соответственно
конце соответственно  и
и  . Здесь используются частные производные, так как ток и напряжение еще функции времени.
. Здесь используются частные производные, так как ток и напряжение еще функции времени.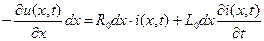

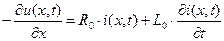 ;
;
 .
.
 - величина комплексная, обозначаемая γ =α+jβ и называемая постоянная распространения длинной линии; α - коэффициент ослабления (затухания); β - коэффициент фазы длинной линии.
- величина комплексная, обозначаемая γ =α+jβ и называемая постоянная распространения длинной линии; α - коэффициент ослабления (затухания); β - коэффициент фазы длинной линии.
 .
.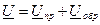 ,
,
 и
и  .
.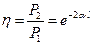
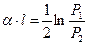 .
.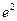 раз, а по напряжению или току – в е
раз, а по напряжению или току – в е  раз. Если рассматривать десятичные логарифмы, то единицы вычислений будут Белл.
раз. Если рассматривать десятичные логарифмы, то единицы вычислений будут Белл.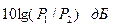 .
.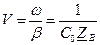 .
.
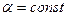 и
и 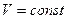 , что обеспечивает отсутствие искажений, необходимо, чтобы
, что обеспечивает отсутствие искажений, необходимо, чтобы 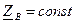 , т.е. чтобы волновое сопротивление не зависело от частоты.
, т.е. чтобы волновое сопротивление не зависело от частоты.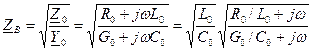 .
.
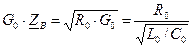 .
.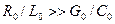 . Поэтому для придания реальным линиям свойств линий без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой.
. Поэтому для придания реальным линиям свойств линий без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой.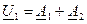
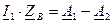
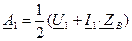
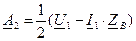
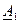 и
и 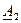 в (5) и (6), получим
в (5) и (6), получим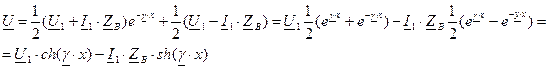
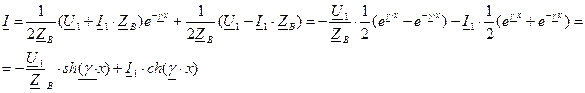
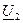 и ток
и ток 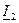 в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде
в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде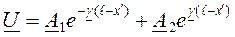 ;
;
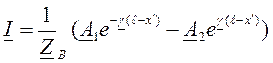 .
.
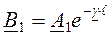 и
и  , из уравнений (9) и (10) при
, из уравнений (9) и (10) при 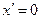 получим
получим

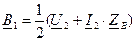
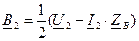
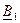 и
и 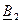 в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии
в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии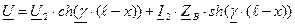 ;
;
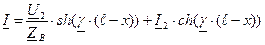 .
.
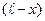 обозначают еще как y.
обозначают еще как y.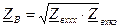
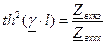 ,
,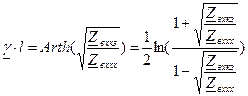 .
.
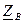 и
и  линии, по которым затем могут быть рассчитаны ее первичные параметры
линии, по которым затем могут быть рассчитаны ее первичные параметры 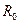 ,
, 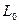 ,
, 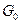 и
и 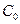 .
. и
и 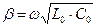 . Таким образом,
. Таким образом,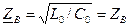
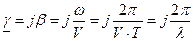 ,
,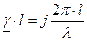 .
. :
: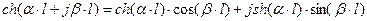
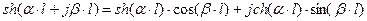
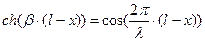 и
и 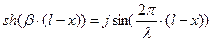 .
.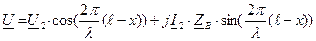 ;
;
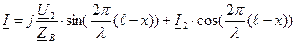 .
.
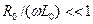 и
и 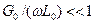 , что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
, что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
 .
.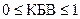 ,
,  .
. – комплексный коэффициент отражения по напряжению.
– комплексный коэффициент отражения по напряжению. ,
,  .
.


