
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, будем иметь в решении две составляющие для действующих значений напряженийСодержание книги
Поиск на нашем сайте
Для тока согласно уравнению (3) можно записать
где Волновое сопротивление Z В и постоянную распространения γ называют вторичными параметрами длинной линии, которые характеризуют ее свойства как устройства для передачи электрического сигнала. Определяя
Слагаемые в правой части соотношения (7) можно трактовать как бегущие волны: первая движется и затухает в направлении возрастания х, вторая убывания х. Действительно, в фиксированный момент времени каждое из слагаемых представляет собой затухающую (вследствие потерь энергии) гармоническую функцию координаты х, а в фиксированной точке – синусоидальную функцию времени. Волну, движущую от начала линии в сторону возрастания х, называют прямой (падающей), а движущуюся от конца линии в направлении убывания х – обратной (отраженной). Коэффициент ослабления показывает как изменяется амплитуда или действующее значение составляющей волны (например прямой волны) на единицу длины в логарифмических единицах На рис. 2 представлена затухающая синусоида прямой волны для моментов времени
Продифференцировав (8) по времени, получим
Длиной волны
Откуда
И с учетом (9)
В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:
где в соответствии с (5)
Представление напряжения в виде суммы прямой и обратной волн согласно (10) означает, что положительные направления напряжения для обеих волн выбраны одинаково: от верхнего провода к нижнему. Аналогично для тока на основании (6) можно записать
Где Положительные направления прямой и обратной волн тока в соответствии с (11) различны: положительное направление прямой волны совпадает с положительным направлением тока На основании (10) и (11) для прямых и обратных волн напряжения и тока выполняется закон Ома в комплексной форме
Бесконечно длинная однородная линия. Согласованный режим работы В случае бесконечно длинной линии в выражениях (5) и (6) для напряжения и тока слагаемые, содержащие e γ x, должны отсутствовать, т.к. стремление х
На основании соотношений (12) можно сделать важный вывод, что для бесконечно длинной линии в любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:
Таким образом, если такую линию мысленно рассечь в любом месте и вместо откинутой бесконечно длинной части подключить сопротивление, численно равное волновому, то режим работы оставшегося участка конечной длины не изменится. Отсюда можно сделать два вывода: Уравнения бесконечно длинной линии распространяются на линию конечной длины, нагруженную на сопротивление, равное волновому. В этом случае также имеют место только прямые волны напряжения и тока. У линии, нагруженной на волновое сопротивление, входное сопротивление также равно волновому. Режим работы длинной линии, нагруженной на сопротивление, равное волновому, называется согласованным, а сама линия называется линией с согласованной нагрузкой.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.212 (0.008 с.) |

 ,
,

 - волновое сопротивление линии.
- волновое сопротивление линии. и
и  , на основании (5) запишем
, на основании (5) запишем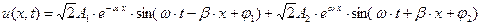 .
.
 Аналогичное уравнение согласно (6) можно записать для тока.
Аналогичное уравнение согласно (6) можно записать для тока. , а коэффициент фазы β=Ψ(x)-Ψ(x+1) – как изменяется фаза составляющей волны на единицу длины в однородной линии.
, а коэффициент фазы β=Ψ(x)-Ψ(x+1) – как изменяется фаза составляющей волны на единицу длины в однородной линии. и
и 
 . Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны:
. Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны: .
.
 .
.
 называется расстояние между двумя ее ближайшими точками, различающимися по фазе на 2
называется расстояние между двумя ее ближайшими точками, различающимися по фазе на 2  рад. В соответствии с данным определением
рад. В соответствии с данным определением ,
,
 .
.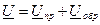 ,
,
 и
и  .
. ,
,
 и
и  .
. (от начала к концу линии), а положительное направление обратной волны ему противоположно.
(от начала к концу линии), а положительное направление обратной волны ему противоположно.
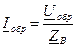
 лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае
лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае 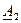 =0. Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным
=0. Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным

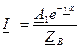
 .
.


