
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стоячие волны в длинных линияхСодержание книги
Поиск на нашем сайте
Как было показано выше, решение уравнений длинной линии можно представить в виде суммы прямой и обратной волн. В результате их наложения в цепях с распределенными параметрами возникают смешанные в том числе и стоячие волны. Рассмотрим два предельных случая: ХХ и КЗ в линии без потерь, когда поглощаемая приемником активная мощность равна нулю. При ХХ на основании уравнений (17) и (18) имеем
Откуда для мгновенных значений напряжения и тока можно записать
При ХХ в соответствии с (19) и (20) в точках с координатами При КЗ на основании уравнений (17) и (18)
Откуда для мгновенных значений можно записать
Т.е. и в этом случае напряжение и ток представляют собой стоячие волны, причем по сравнению с режимом ХХ пучности и узлы напряжения и тока соответственно меняются местами. Поскольку в узлах мощность тождественно равна нулю, стоячие волны в передаче энергии вдоль линии не участвуют. Ее передают только бегущие волны. Чем сильнее нагрузка отличается от согласованной, тем сильнее выражены обратные и, следовательно, стоячие волны. В рассмотренных предельных случаях ХХ и КЗ имеют место только стоячие волны, и мощность на нагрузке равна нулю. Волновое сопротивление длинной линии. Волновое сопротивление Волновое сопротивление не зависит от длины линии, а определяется ее первичными параметрами. Определим модуль и аргумент волнового сопротивления соответственно:
Самостоятельно определить ωm! Ответ: Используя уравнения передачи вида:
определим напряжение и ток в начале линии при согласованном режиме, когда
Поскольку Окончательно получим:
Из последних уравнений легко определить напряжение и ток в конце линии:
Напряжение и ток в любой точке линии при согласованном режиме определяются:
8.9. Коэффициент распространения. Способ определения первичных параметров Коэффициент распространения:
Определим модуль и аргумент коэффициента распространения соответственно:
При согласованном режиме
Пусть
Рассмотрим способ определения первичных параметров по известным вторичным параметрам. Т.к.
Таким образом:
Вопрос № 32 Входное сопротивление длинной линии Входное сопротивление
Рассмотрим частные случаи режима работы линии. При согласованном режиме работы В режиме короткого замыкания
В режиме холостого хода
На практике удобно входное сопротивление линии выражать через параметры холостого хода и короткого замыкания, т.е.
Представим зависимость модулей сопротивлений XX и КЗ от длины линии и зависимость модуля
Выводы: Колебательный характер входного сопротивления при несогласованном режиме объясняется наличием в линии падающих и отраженных волн. При изменении частоты и длины линии изменяется фаза отраженной волны. Если в начале линии отраженная и падающая волна напряжения совпадают по фазе (отраженная и падающая волна тока находятся в противофазе), то
Если в начале линии отраженная и падающая волна напряжения находятся в противофазе (отраженная и падающая волна тока совпадают по фазе), то
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.27 (0.009 с.) |

 и
и 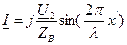 ,
, ;
;
 .
.
 Последние уравнения представляют собой уравнения стоячих волн, являющихся результатом наложения прямой и обратной волн с одинаковыми амплитудами.
Последние уравнения представляют собой уравнения стоячих волн, являющихся результатом наложения прямой и обратной волн с одинаковыми амплитудами. , где k - целое число, имеют место максимумы напряжения, называемые пучностями, и нули тока, называемые узлами. В точках с координатами
, где k - целое число, имеют место максимумы напряжения, называемые пучностями, и нули тока, называемые узлами. В точках с координатами 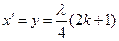 пучности и узлы напряжения и тока меняются местами (см. рис. 2). Таким образом, узлы и пучности неподвижны, и пучности одной переменной совпадают с узлами другой и наоборот.
пучности и узлы напряжения и тока меняются местами (см. рис. 2). Таким образом, узлы и пучности неподвижны, и пучности одной переменной совпадают с узлами другой и наоборот.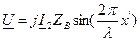 и
и  ,
,

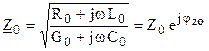 .
. ,
,  .
. Построим графическую зависимость
Построим графическую зависимость  и
и  . Для всех реально существующих линий
. Для всех реально существующих линий 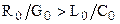 , поэтому:
, поэтому: .
. ,
,  ,
,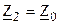 , где
, где  – сопротивление нагрузки:
– сопротивление нагрузки: ,
,  ,
, ,
, 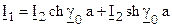 ,
, ,
,  .
. ,
,  , тогда
, тогда  .
. ,
,  .
. ,
,  .
. ,
,  .
. , откуда
, откуда – коэффициент ослабления,
– коэффициент ослабления, 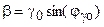 – коэффициент фазы.
– коэффициент фазы. ,
,  .
. Построим графическую зависимость
Построим графическую зависимость  и
и  .
. .
. ,
,  ,
,  ,
, 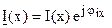 , тогда
, тогда , следовательно
, следовательно ,
,  , откуда определяем:
, откуда определяем: [Нп/м], либо
[Нп/м], либо  [дБ/м]
[дБ/м] , для линии длинной x = 1м, получаем
, для линии длинной x = 1м, получаем  [рад/м].
[рад/м]. ,
, 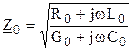 , то
, то ,
, 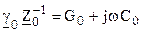 .
. ,
,  ,
,  ,
,  .
. линии определяется отношением напряжения и тока в начале линии. Определим входное сопротивление с помощью уравнений передачи:
линии определяется отношением напряжения и тока в начале линии. Определим входное сопротивление с помощью уравнений передачи: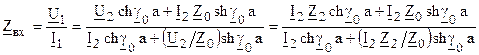 , после преобразований
, после преобразований
 .
. , тогда
, тогда .
.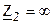 , тогда
, тогда .
. и
и  .
. ,
,

 .
.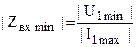 .
.


