Цепи с сосредоточенными параметрами – здесь привычные параметры сопротивления, индуктивности и емкости сосредоточены в локальных точках цепи

2) цепи с распределенными параметрами- здесь привычные параметры сопротивления, индуктивности и емкости не сосредоточены в локальных точках цепи, а распределены по ее объему. В таких цепях не применимы непосредственно законы Кирхгофа для токов и напряжений, а следует использовать законы электромагнитного поля (уравнения Максвелла).

Для оценки, к какому типу отнести цепь с сосредоточенными или распределенными параметрами – следует сравнить ее геометрические размеры с длиной электромагнитной волны λ=V▪T=V/f. Если размеры цепи сопоставимы с l>0,1……0,25∙ λ, то цепь следует рассматривать как цепь с распределенными параметрами, так как здесь нельзя пренебречь временем распространения электромагнитного колебания (волны) по цепи.

Если только длина цепи сопоставима с четвертью длины волны, а остальные параметры не сопоставимы, то такую цепь называют длинной линией. Например, для ƒ=5OΓц, т.е. при Т=0.02c и V=3▪10⁸м/c, λ = 6000▪10³м

и λ/4=1500 км. Для ƒ=10⁸Гц λ/4=0,75м, т.е. уже при l=0,5м к цепи следует подходить как к цепи с распределенными параметрами, так как здесь нельзя пренебречь временем распространения волны.

Длинная линия (линия передачи) – устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии в заданном направлении. Линия называется регулярной, если в продольном направлении неизменны ее поперечное сечение, положение ее в пространстве и электромагнитные свойства заполняющих ее сред. Линия является однородной, если в произвольном поперечном сечении параметры среды неизменны.

Для исследования процессов в цепи с распределенными параметрами (в основном длинных линий) введем дополнительное условие о равномерности распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости и проводимости. Такую линию называют однородной. Линию с неравномерным распределением параметров часто можно разбить на однородные участки.

Уравнения однородной линии в стационарном режиме

Под первичными параметрами линии будем понимать сопротивление R₀ (Ом/м) индуктивность L₀ (Гн/м), проводимость G₀ (g_o) (Cм/м) и емкость C₀ (Ф/м), отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины dх << λ/4 со структурой, показанной на рис. 1, где переменная х показывает расстояние от начала линии. Здесь уже можно применить законы Кирхгофа. Пусть напряжение и ток в начале такого элементарного участка равны u и i, а в конце соответственно и . Здесь используются частные производные, так как ток и напряжение еще функции времени.

Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа с учетом, что ток и напряжение следует рассматривать функциями двух переменных координаты х и времени t получим

или после сокращения на dx

;

(1)

.

(2)

Эти уравнения называют телеграфными, так как были рассмотрены при исследовании передачи телеграфных сообщений.

Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при ƒ=0 можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока. При гармоническом воздействии, вводя комплексные величины и заменяя ∂⁄∂t на jω, на основании (1) и (2) получаем

-d U ⁄dx=(Ro+jωLo) ∙ I = Ζ o∙ I;

(3)

-d I ⁄dx=(Go+jωCo) ∙ U = Y o∙ U

(4)

Где Ζ _o = R_o+jωL_o и Y _o=G_o+jωC_o - соответственно комплексные продольное сопротивление и поперечная проводимость схемы замещения на единицу длины линии.

Продифференцировав (3) по х и подставив выражение d I ⁄dx из (4), запишем

d² U ⁄dx² = Ζ o∙ Y o∙ U

Характеристическое уравнение

p² - Ζ o∙ Y o=0,

Откуда

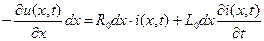
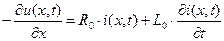p=± - величина комплексная, обозначаемая γ =α+jβ и называемая постоянная распространения длинной линии; α - коэффициент ослабления (затухания); β - коэффициент фазы длинной линии.