
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отметим, что данный режим практически важен для передачи информации, поскольку характеризуется отсутствием отраженных (обратных) волн, обусловливающих искажение передаваемого сигнала (помехи).Содержание книги
Поиск на нашем сайте Согласованная нагрузка полностью поглощает мощность волны, достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом сечении согласованной линии сопротивление равно волновому, угол сдвига
Откуда КПД линии
И ослабление
Как указывалось при рассмотрении четырехполюсников, единицей ослабления является непер, соответствующий затуханию по мощности в Принято использовать 10 часть, то есть децибелы Линия без искажений Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для его гармонических составляющих ослабление и фазовая скорость различны, т.е. если последние являются функциями частоты. Таким образом, для отсутствия искажений, что очень важно, например, в линиях передачи информации, необходимо, чтобы все гармоники распространялись с одинаковой скоростью и одинаковым ослаблением, поскольку только в этом случае, сложившись, они образуют в конце линии сигнал, подобный входному. Идеальным в этом случае является так называемая линия без потерь, у которой сопротивление R0 и проводимость G0 равны нулю. Действительно, в этом случае
т.е. независимо от частоты коэффициент ослабления
Однако искажения могут отсутствовать и в линии с потерями. Условие передачи сигналов без искажения вытекает из совместного рассмотрения выражений для постоянной распространения
И фазовой скорости
Из (1) и (2) вытекает, что для получения
Как показывает анализ (3), при
Линия, параметры которой удовлетворяют условию (4), называется линией без искажений. Фазовая скорость для такой линии
И ослабление
Следует отметить, что у реальных линий (и воздушных, и кабельных) Уравнения линии конечной длины
Определяются на основании граничных условий. Пусть для линии длиной l (см. рис. 1) заданы напряжение Тогда из (5) и (6) получаем
Откуда
Подставив найденные выражения
Уравнения (7) и (8) позволяют определить ток и напряжение в любой точке линии по их известным значениям в начале линии. Обычно в практических задачах бывают заданы напряжение
Обозначив
Откуда
После подстановки найденных выражений
Координату Уравнения длинной линии как четырехполюсника В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения. Определение параметров длинной линии из опытов холостого хода и короткого замыкания Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ). При ХХ
При КЗ
На основании (13) и (14)
и
Откуда
Выражения (15) и (16) на основании данных эксперимента позволяют определить вторичные параметры Линия без потерь Линией без потерь называется линия, у которой первичные параметры
откуда Раскроем гиперболические функции от комплексного аргумента
Тогда для линии без потерь, т.е. при Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |

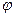 между напряжением и током неизменен. Таким образом, если активная мощность, получаемая линией от генератора, равна
между напряжением и током неизменен. Таким образом, если активная мощность, получаемая линией от генератора, равна 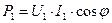 , то мощность в конце линий длиной l в данном случае
, то мощность в конце линий длиной l в данном случае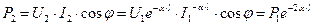 ,
,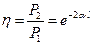
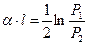 .
.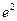 раз, а по напряжению или току – в е
раз, а по напряжению или току – в е  раз. Если рассматривать десятичные логарифмы, то единицы вычислений будут Белл.
раз. Если рассматривать десятичные логарифмы, то единицы вычислений будут Белл.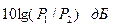 .
.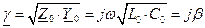 ,
,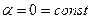 и фазовая скорость
и фазовая скорость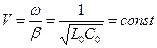 .
.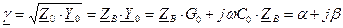
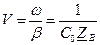 .
.
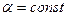 и
и 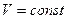 , что обеспечивает отсутствие искажений, необходимо, чтобы
, что обеспечивает отсутствие искажений, необходимо, чтобы 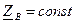 , т.е. чтобы волновое сопротивление не зависело от частоты.
, т.е. чтобы волновое сопротивление не зависело от частоты.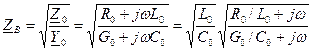 .
.
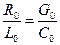
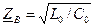 есть вещественная константа.
есть вещественная константа.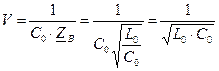
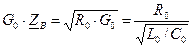 .
.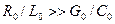 . Поэтому для придания реальным линиям свойств линий без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой.
. Поэтому для придания реальным линиям свойств линий без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой. Постоянные
Постоянные 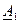 и
и 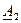 в полученных в предыдущей лекции формулах
в полученных в предыдущей лекции формулах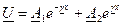 ;
;
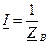 (
(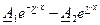 )
)
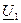 и ток
и ток  в начале линии, т.е. при x=0.
в начале линии, т.е. при x=0.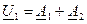
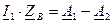
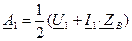
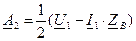
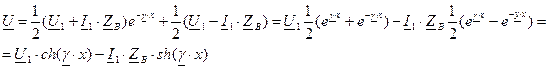
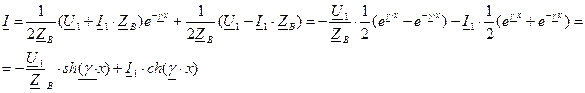
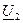 и ток
и ток 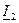 в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде
в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде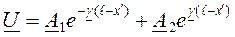 ;
;
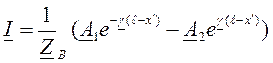 .
.
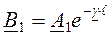 и
и  , из уравнений (9) и (10) при
, из уравнений (9) и (10) при 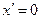 получим
получим

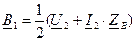
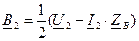
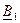 и
и 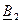 в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии
в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии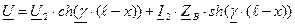 ;
;
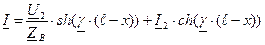 .
.
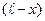 обозначают еще как y.
обозначают еще как y.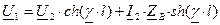 ;
;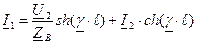 .
.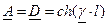 ;
; 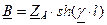 и
и 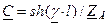 ; при этом условия
; при этом условия 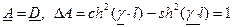 выполняются.
выполняются.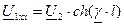 и
и  , откуда входное сопротивление
, откуда входное сопротивление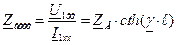 .
.
 и
и 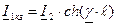 . Следовательно,
. Следовательно,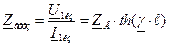 .
.
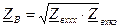
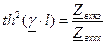 ,
,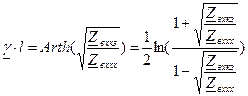 .
.
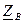 и
и  линии, по которым затем могут быть рассчитаны ее первичные параметры
линии, по которым затем могут быть рассчитаны ее первичные параметры 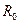 ,
, 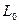 ,
, 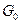 и
и 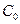 .
. и
и 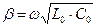 . Таким образом,
. Таким образом,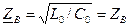
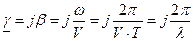 ,
,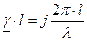 .
. :
: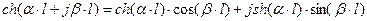
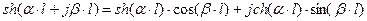
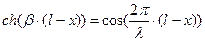 и
и 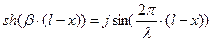 .
.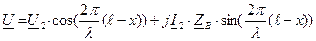 ;
;
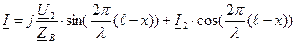 .
.
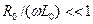 и
и 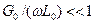 , что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
, что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).


