
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переходные процессы в цепях первого порядкаСодержание книги
Поиск на нашем сайте
8.1 Цель работы: изучение переходных процессов в последовательных RL- и RC-линейных цепях при воздействии на них прямоугольных импульсов напряжения.
8.2 Оборудование и материалы: электрический стенд для исследования переходных процессов в последовательных RL и RC линейных цепях, генератор прямоугольных импульсов, осциллограф CI-72 или CI-73. Принципиальная электрическая схема стенда приведена на рисунке 8.1. С помощью гнёзд 1-17 и электрических проводников между входом и выходом стенда обеспечивается включение цепи, состоящей из резистора R и конденсатора С или из резистора R и индуктивности L. Упрощенные принципиальные схемы стенда, необходимые для выполнения работы, приведены на рисунках 8.2, 8.3. Схема рисунка 8.2а образуется путём соединения электрическими проводами гнезд 6 и 8, 7 и 9, 12 и 13. Схема рисунка 8.3а образуется соединением между собой гнёзд 8 и 10, 9 и 11, 12 и 13. Для получения схемы рисунка 8.3б соединяются гнезда 8 и 10, 9 и 11, 3 и 13. Гнезда 1, 2 (вход стенда) предназначены для подключения генератора импульсов, гнезда 18, 17 (выход стенда) – для подключения входа «У» осциллографа.
Рисунок 8.1 – Принципиальная схема стенда
Рисунок 8.2 – Упрощенные принципиальные схемы стенда (RC-цепь)
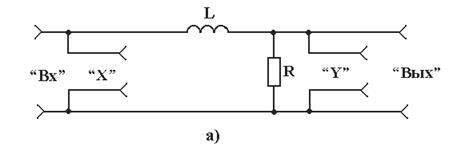
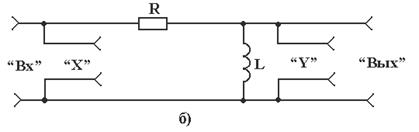
Рисунок 8.3 – Упрошенные принципиальные схемы стенда (RL-цепь)
Рисунок 8.4 – Временная диаграмма напряжения на выходе генератора
С выхода генератора на вход стенда подаются импульсы напряжения прямоугольной формы, период следования которых превышает время практического затухания переходных процессов в исследуемых цепях. Длительность импульсов принимает два значения tu
Сведения из теории В цепи, содержащей реактивные элементы, при переходе от одного стационарного состояния к другому появляются так называемые переходные процессы. Возникновение переходных процессов связано с тем, что изменение энергии электромагнитного поля в реактивных элементах при переходе к новому стационарному состоянию происходит во времени плавно, без скачков. И в результате выходной ток и напряжение будут отличаться по форме от внешнего воздействия.
При изучении многих импульсных устройств приходится исследовать переходные процессы в цепях, содержащих один реактивный элемент (С или L), которые описываются неоднородным дифференциальным уравнением первого порядка:
где х (t) – искомая функция времени (напряжение или ток);
у (t) – напряжение (ток) внешнего источника. Решение уравнения (8.1) имеет вид:
Характер частного решения В решении уравнения (4.1) функция Таким образом, переходный процесс в общем случае представляет собой совокупность свободной и вынужденной составляющих токов и напряжений, которые должны быть связаны между собой посредством начальных условий. Переходные процессы в цепи с одним реактивным элементом – конденсатором С, т.е. в RC- цепи (рисунке 8.2а) описываются уравнением:
где uR (t) – напряжение на резисторе R; u (t) – напряжение на входе цепи; При подаче на вход RC-цепи (рисунок 8.2а) прямоугольного импульса напряжения (рисунок 8.5а) в момент времени В течение времени
Скорость заряда ёмкости зависит от постоянной времени цепи: чем больше величины емкости С и активного сопротивления R, тем медленнее растет напряжение uc. Напряжение на активном сопротивлении (рисунок 8.5в) в момент времени
В момент времени
Рисунок 8.5 – Переходные процессы в RC-цепи при подаче на вход прямоугольных импульсов
В случае, если постоянная времени цепи При достаточно малом значении
и тогда уравнение (8.2) принимает вид:
То есть напряжение на резисторе пропорционально первой производной входного напряжения. Поэтому цепь, изображенную на рисунке 8.2а, называют дифференцирующей, если RC < tu.
Рисунок 8.6 – Временные диаграммы напряжений на резисторе и ёмкости при
В случае, если постоянная времени цепи В установившемся режиме напряжение u c(t) колеблется около среднего значения входного напряжения u (t) и в данном случае представляет собой отрезок нарастающей и убывающей экспонент.
Рисунок 8.7 – Временные диаграммы напряжений на резисторе и ёмкости при τ > t и
Во время действия импульса, в соответствии с формулой (4.3), u c(t) нарастает от U 1 до U 2 по закону:
Во время паузы напряжение u c(t) падает от U 2= Е по закону (8.5):
Если
или
т.е. переменная составляющая напряжения на сопротивлении, повторяет форму переменной составляющей напряжения на входе. Поэтому цепь, изображенную на рисунке 8.2а, называют неискажающей, если Нетрудно показать, что напряжение на емкости неискажающей цепи (рисунке 8.2б) пропорционально интегралу входного напряжения u (t). Известно, что
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.007 с.) |





 = 10
= 10  c и tu
c и tu  = 0,5´10
= 0,5´10 
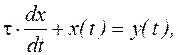 (8.1)
(8.1)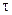 – постоянная времени цепи;
– постоянная времени цепи;
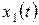 зависит от вида внешнего воздействия, т.е.
зависит от вида внешнего воздействия, т.е. 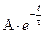 характеризует электрические явления, обусловленные изменением начального энергетического состояния цепи в отсутствии вынужденного воздействия, называемые собственными (или свободными) процессами.
характеризует электрические явления, обусловленные изменением начального энергетического состояния цепи в отсутствии вынужденного воздействия, называемые собственными (или свободными) процессами. (8.2)
(8.2) – постоянная времени цепи.
– постоянная времени цепи. происходит скачкообразное изменение входного напряжения от 0 до Е.
происходит скачкообразное изменение входного напряжения от 0 до Е.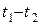 ёмкость заряжается, и напряжение на ней в процессе заряда возрастает по экспоненциальному закону, стремясь к величине Е (рисунок 8.5б):
ёмкость заряжается, и напряжение на ней в процессе заряда возрастает по экспоненциальному закону, стремясь к величине Е (рисунок 8.5б):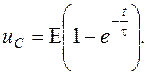 (8.3)
(8.3)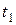 изменяется скачком от нуля до максимума, а далее в течение времени
изменяется скачком от нуля до максимума, а далее в течение времени 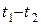 убывает по экспоненциальному закону:
убывает по экспоненциальному закону: (8.4)
(8.4) напряжение на входе RC-цепи скачкообразно изменяется от Е до 0. При
напряжение на входе RC-цепи скачкообразно изменяется от Е до 0. При  напряжение на входе цепи равно нулю и в RC-цепи будут наблюдаться только свободные явления: емкость С, заряженная до какого-то напряжения
напряжение на входе цепи равно нулю и в RC-цепи будут наблюдаться только свободные явления: емкость С, заряженная до какого-то напряжения 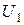 , разряжается на активное сопротивление R по экспоненциальному закону:
, разряжается на активное сопротивление R по экспоненциальному закону: (8.5)
(8.5)
 меньше длительности прямоугольного импульса
меньше длительности прямоугольного импульса 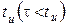 , переходные процессы в цепи практически успевают затухнуть за время длительности импульса, и временные диаграммы напряжений на резисторе и на конденсаторе имеют вид, изображенный на рисунке 8.6, где Е – высота входного импульса;
, переходные процессы в цепи практически успевают затухнуть за время длительности импульса, и временные диаграммы напряжений на резисторе и на конденсаторе имеют вид, изображенный на рисунке 8.6, где Е – высота входного импульса; 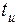 – длительность входного импульса;
– длительность входного импульса;  – длительность выходного импульса на уровне 0,1 Е.
– длительность выходного импульса на уровне 0,1 Е. , получаем:
, получаем:
 (8.5)
(8.5)
 <
< 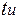
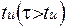 , переходные процессы не успевают закончиться за время длительности импульса, поэтому напряжения на конденсаторе и сопротивлении будут иметь вид, изображенный на рисунке 8.7.
, переходные процессы не успевают закончиться за время длительности импульса, поэтому напряжения на конденсаторе и сопротивлении будут иметь вид, изображенный на рисунке 8.7.

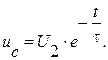
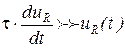 и уравнение (8.2) принимает вид:
и уравнение (8.2) принимает вид: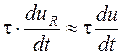
 , (8.6)
, (8.6) .
. . (8.7)
. (8.7)


