
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование переходных процессов в цепяхСодержание книги
Поиск на нашем сайте
ВТОРОГО ПОРЯДКА
9.1 Цель работы: изучение переходных процессов в последовательном колебательном контуре при воздействии на него прямоугольных импульсов напряжения.
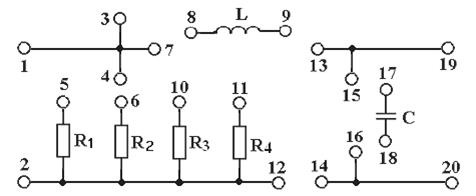
9.2 Оборудование и материалы: электрический стенд для исследования переходных процессов, генератор прямоугольных импульсов напряжения, осциллограф CI-72, милливольтметр В3-33. Принципиальная схема стенда приведена на рисунке 9.1
Рисунок 9.1 – Принципиальная схема стенда
С помощью гнезд 1-17 и электрических проводников обеспечивается подключение элементов R, L, C к стенду. Схема исследуемой цепи второго порядка (последовательный колебательный контур) представлена на рисунке 9.2.
Рисунок 9.2 – Схема цепи второго порядка
С выхода генератора на вход стенда подаются импульсы напряжения прямоугольной формы, период следования которых Т имеет фиксированную величину и в десять раз превышает период Т св свободных колебаний исследуемой цепи.
Сведения из теории Пусть в момент времени t = 0 к RLC-цепи подключается источник э.д.с. e(t). Уравнение, описывающее переходный процесс, запишется в виде:
Дифференцируя это уравнение, получим:
Соответствующее ему характеристическое уравнение определяется выражением:
Корни этого уравнения:
где Свободный ток будет равен:
где А1 и А2 – постоянные коэффициенты. Ток в цепи определяется суммой свободного iсв и установившегося iу токов:
Для нахождения iу необходимо знать конкретный вид входного воздействия e(t). Будем считать, что ко входу цепи подключается источник постоянной э.д.с Е. Пусть в момент времени t = 0 напряжение на емкости uC (0) =U0 и ток цепи i (0)=0. Для определения постоянных A1 и A2 наряду с независимым начальном условием i (0)=0 необходимо знать и зависимое начальное условие Найдем это условие. Уравнение (9.1) для t = 0 имеет вид:
Откуда
При e(t)=Е уравнение (9.2) запишется в виде:
Правая часть уравнения (9.5) равна нулю, поэтому и установившееся значение тока цепи iy также будет равно нулю. Дифференцируя выражение (9.3) с учетом iy= 0, получим:
Из выражений (9.3) и (9.6) для t = 0 получим:
Откуда следует:
Окончательно выражение для тока запишется в виде:
Проанализируем полученное решение для трёх возможных случаев:
а) б) в) Для случая а) корни р1 и р2 характеристического уравнения являются отрицательными действительными числами (рисунок 9.3). Если
Рисунок 9.3 – Расположение действительных корней на комплексной плоскости
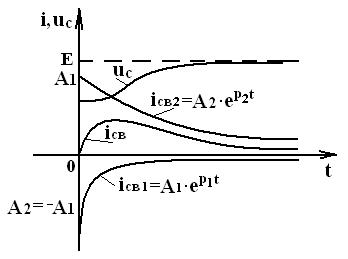
Рисунок 9.4 – Графики изменения тока цепи и напряжения на ёмкости в последовательном колебательном контуре при е (t) = E, когда p 1 и p 2 действительны
Рассмотрим второй случай (случай б). При Подстановка этого значения в выражение (9.7) приводит к неопределенности типа
Кривая тока i(t) для этого случая имеет такой же вид, как и на рисунке 9.4. Рассмотрим третий случай (случай в)). Корни характеристического уравнения комплексные и сопряженные (рисунок 9.5):
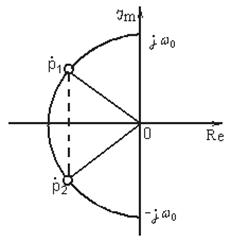
где Корни уравнения располагаются симметрично относительно действительной оси в левой полуплоскости на полуокружности с центром в начале координат и с радиусом
Рисунок 9.5 – Расположение комплексно сопряжённых корней на комплексной плоскости
Величина
Кривая зависимости i(t) показана на рисунке 9.6.
Рисунок 9.6 – Графики изменения тока цепи и напряжения на ёмкости в последовательном колебательном контуре при колебательном характере переходного процесса
Из выражения (9.8) и рисунка 9.6 видно, что при О быстроте затухания колебательного процесса судят по величине Величину
Из сопоставления рисунков 9.3 и 9.5 видно, что о характере переходного процесса можно судить по расположению корней характеристического уравнения на комплексной плоскости. Если корни различны и лежат на действительной оси, то имеет место апериодический процесс. Если
Подготовка к лабораторной работе 9.4.1 При выполнении расчетов к лабораторной работе следует считать, что параметры колебательного контура L = 50 мГн и С = 0,1 мкФ остаются неизменными в процессе выполнения работы, а сопротивление R принимает четыре значения: 510 Ом, 1 кОм, 1,5 кОм и 3 кОм. 9.4.2 Рассчитать значение критического сопротивления контура: R кр. 9.4.3 Найти корни характеристического уравнения для R = 510 Ом, 1кОм, 1,5 кОм, 3 кОм. 9.4.4 Найти частоты свободных колебаний исследуемого контура
Порядок выполнения работы 9.5.1 Подключить вход осциллографа к выходу генератора и получить на экране устойчивое изображение 1-2 импульсов напряжения генератора, используя внутреннюю синхронизацию. Период следования импульсов должен быть в 10 раз больше периода свободных колебаний. Определить масштаб изображения. 9.5.2 Подключить генератор ко входу последовательного колебательного контура с R = 510 Ом, а вход осциллографа – к выводам конденсатора С. Зарисовать полученную осциллограмму. 9.5.3 Повторить п.п. 9.5.1, 9.5.2 для R = 1 кОм ( 9.5.4 Повторить п. 9.5.3 для R = 1,5 кОм. 9.5.5 Повторить п. 9.5.3 для R = 3 кОм.
Обработка результатов 9.6.1 На основании полученных осциллограмм напряжения найти частоты свободных колебаний 9.6.2 Определить корни характеристического уравнения, соответствующие экспериментальным кривым в колебательном режиме. Сравнить их со значениями, найденными расчетным путем. 9.6.3 Вычислить абсолютные и относительные погрешности полученных результатов.
Контрольные вопросы: 1. Чем определяется порядок цепи при расчете переходных процессов? 2. В каких случаях свободная составляющая напряжения на конденсаторе имеет колебательный характер, а в каких – апериодический? 3. Чем определяется частота свободных колебаний контура? 4. Как определяется постоянная времени последовательного колебательного контура? 5. Чем определяется декремент затухания и логарифмический декремент затухания колебаний? 6. Можно ли избежать возникновения переходного процесса в последовательном колебательном контуре? 7. В чем заключается преимущество и недостатки классического метода расчета переходных процессов? 8. Как изменится величина – сопротивление контура R; – индуктивность L; – ёмкость С? 9. Чем определяется длительность переходного процесса в последовательном колебательном контуре? 10. Как связан характер протекания переходного процесса в последовательном колебательном контуре с расположением корней характеристического уравнения на комплексной плоскости? Рекомендуемая литература [1, с. 87–295; 2, c. 346–362; 3, c. 427–445].
Лабораторная работа № 10
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.77.149 (0.008 с.) |


 (9.1)
(9.1) (9.2)
(9.2)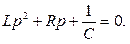
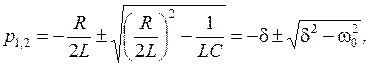
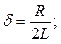
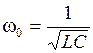 – резонансная частота контура.
– резонансная частота контура.
 (9.3)
(9.3)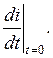
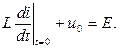
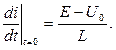 (9.4)
(9.4)
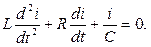 (9.5)
(9.5)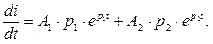 (9.6)
(9.6)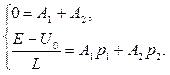
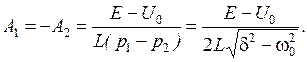
 (9.7)
(9.7)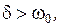 т.е.
т.е. 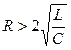 (процесс апериодический);
(процесс апериодический); т.е.
т.е.  (критический случай);
(критический случай); т.е.
т.е. 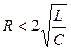 (процесс колебательный).
(процесс колебательный). то кривая
то кривая 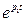 спадает медленнее, чем кривая
спадает медленнее, чем кривая  . Кривые i(t) и uC(t) показаны на рисунке 9.4.
. Кривые i(t) и uC(t) показаны на рисунке 9.4.


 . Раскроем ее по правилу Лоппиталя:
. Раскроем ее по правилу Лоппиталя: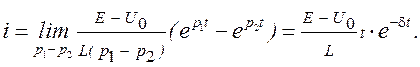



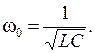
 называется угловой частотой свободных колебаний в RLC - цепи. Выражение для тока i(t) запишется в виде:
называется угловой частотой свободных колебаний в RLC - цепи. Выражение для тока i(t) запишется в виде: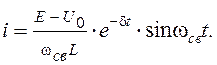 (9.8)
(9.8)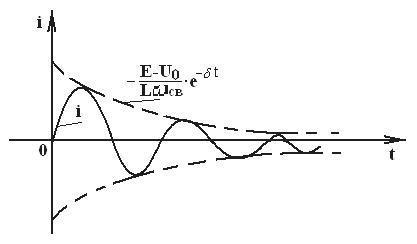
 в цепи возникают затухающие синусоидальные колебания, причем огибающими служат кривые
в цепи возникают затухающие синусоидальные колебания, причем огибающими служат кривые  . Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и наоборот, причем, эти колебания сопровождаются потерей энергии в сопротивлении. Чем меньше
. Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и наоборот, причем, эти колебания сопровождаются потерей энергии в сопротивлении. Чем меньше  по сравнению с
по сравнению с  , тем медленнее затухает колебательный процесс и тем ближе
, тем медленнее затухает колебательный процесс и тем ближе  называемой декрементом колебания, где
называемой декрементом колебания, где  Кроме того, для этих же целей используется логарифмический декремент колебания
Кроме того, для этих же целей используется логарифмический декремент колебания 
 называют постоянной времени колебательного контура:
называют постоянной времени колебательного контура:
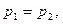 то имеет место критический случай. Для р1 и р2 комплексно сопряженных имеет место колебательный процесс.
то имеет место критический случай. Для р1 и р2 комплексно сопряженных имеет место колебательный процесс. для R = 510 Ом и
для R = 510 Ом и  для R =1 кОм.
для R =1 кОм.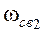 ).
). ,
,  и критическое сопротивление
и критическое сопротивление  . Сравнить их с расчетными значениями.
. Сравнить их с расчетными значениями. , если увеличить:
, если увеличить:


