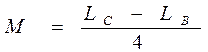Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи со взаимной индуктивностьюСодержание книги
Поиск на нашем сайте
3.1 Цель работы: исследование характеристик цепей с взаимной индуктивностью. 3.2 Оборудование и материалы: электрический стенд для исследования цепей со взаимной индуктивностью, генератор «Электроника», милливольтметр В3-33. Принципиальная электрическая схема стенда представлена на рисунке 3.1. С помощью гнезда 1,…12 и соединительных проводов между гнездами 1, 2 (вход) и 3, 4 или 9, 10 (выход) стенда обеспечиваются включение одной из исследуемых цепей. Упрощенные принципиальные схемы стенда приведены на рисунках 3.2 – 3.3 Схемы рисунков 3.2 и 3.3а образуются путем подключения выводов индуктивностей L 1 и L 2 или последовательно соединенных индуктивностей L 1 и L 2 к гнездам 5, 6. Для получения схемы рисунка 3.3б индуктивность L 1 подключается к гнездам 5, 6, индуктивность L 2 – к гнездам 7, 8. Для получения схемы рисунка 3.3в необходимо соединить между собой гнезда 11, 12.
Рисунок 3.1 – Принципиальная схема стенда
Рисунок 3.3 – Упрощенные принципиальные схемы стенда
При выполнении лабораторного задания возникает необходимость в измерении тока через индуктивность. В настоящей работе такое измерение выполняется косвенно. Последовательно с индуктивностью включается один из резисторов R 1 или R 2, сопротивление каждого из которых (300 Ом) значительно меньше индуктивного сопротивления катушки и практически не влияет на величину тока в цепи. О величине тока судят по напряжению на сопротивлении. Гнезда 1, 2 (вход) предназначены для подключения низкочастотного генератора. Напряжение на входе стенда устанавливается и контролируется по измерительному прибору генератора или с помощью милливольтметра, подсоединенного к гнездам 1, 3. Гнезда «Вых» предназначены для подключения милливольтметра к выходу исследуемой цепи. В качестве гнезд «Bыx» используются гнезда 3, 4 или 9, 10.
Сведения из теории Две электрические цепи называются индуктивно связанными, если в них находятся э.д.с. взаимной индукции. Индуктивная связь между такими цепями характеризуется взаимной индуктивностью М, равной отношению потокосцепления взаимной индукции в одной цепи к току в другой:
где
Для линейных электрических цепей Положительные направления токов i 1 и i 2 в двух индуктивно связанных катушках считают согласными, если положительные направления создаваемых ими магнитных потоков самоиндукции Ф1, Ф2 и взаимной индукции
Рисунок 3.4 – Согласное направление токов в индуктивно связанных Катушках
Рисунок 3.5 – Встречное направление токов в индуктивно связанных катушках
При согласном направлении токов i 1 и i 2 в двух индуктивно связанных катушках выводы этих катушек, относительно которых токи направлены одинаково, называются одноименными или однополярными. На рисунках 3.4, 3.5 эти выводы обозначены точками. Одноименные выводы индуктивно связанных катушек характеризуются тем, что при одинаковом направлении токов i 1 и i 2 относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждой катушке складываются. Поэтому при изображении электрических принципиальных схем электрических устройств намотка витков индуктивно связанных катушек не показывается, а обозначаются их одноименные выводы. При последовательном согласном включении двух индуктивно связанных катушек (рисунок 3,6а) суммарное мгновенное значение напряжения u c будет равно:
где
Последовательное включение катушек индуктивности.
Рисунок 3.6 – Способы включения катушек индуктивности: а) согласное включение; б) встречное включение
Индуктивность цепи
При последовательном встречном включении двух индуктивно связанных катушек (рисунок 3.6 б) суммарное мгновенное значение напряжения будет равно:
где Индуктивность цепи
Если в цепи с индуктивно связанными катушками действует гармоническая э.д.с., то расчет такой цепи проводят методом комплексных амплитуд. Выражения (3.3), (3.5) будут иметь тогда следующий вид:
Из выражений (3.7), (3.8) можно легко найти токи
Если
Величина Для количественной характеристики двух индуктивно связанных катушек используется коэффициент связи k определяемый выражением:
Две индуктивно связанные и включенные параллельно катушки индуктивности без сердечника образуют воздушный трансформатор (рисунок 3.7). Если токи и напряжения на входе и выходе трансформатора обозначить через
Рисунок 3.7 – Электрическая схема воздушного трансформатора
Определяя из выражения (3.15) ток
Третье слагаемое в выражении (3.15) представляет собой комплексное сопротивление
Схема замещения трансформатора представлена на рисунке 3.8. Если сопротивление нагрузки активно
Рисунок 3.8 – Схема замещения воздушного трансформатора
Активная
В режиме холостого хода
Ток в первичной обмотке трансформатора
Величина n, определяемая как отношение напряжений
Подготовка к лабораторной работе 3.4.1 Рассчитать индуктивность двух одинаковых катушек L 1 и L 2 и взаимную индуктивность М между ними по заданным индуктивностям при согласного 3.4.2 Рассчитать действующее значение тока в цепи (рисунок 3.3а) при согласном и встречном включении катушек L 1 и L 2. Индуктивности 3.4.3 Для воздушного трансформатора, изображенного на рисунке 3.3б, в, рассчитать, используя результаты п. 3.4.1, напряжение на вторичной обмотке и ток через первичную обмотку при отключенной нагрузке R2, то есть в режиме холостого хода. Величинами 3.4.4 Используя результаты п. 3.4.1, рассчитать активную Величины R 2=300 Ом,
Порядок выполнения работы 3.5.1 Установить на входе стенда гармонический сигнал частотой 3.5.2 С целью вычисления индуктивности L 1 определить ток через нее, для чего собрать схему, представленную на рисунке 3.2а, и измерить напряжение на резисторе R 1. 3.5.3 Для вычисления индуктивности катушки L 2 собрать схему, изображенную на рисунке 3.2б, и измерить напряжение на резисторе R 1. 3.5.4 Для вычисления индуктивности согласно включенных катушек L 1 и L 2 собрать схему, представленную на рисунке 3.3а, катушки включить согласно и измерить напряжение на резисторе R 1. 3.5.5 Для определения индуктивности встречно включенных катушек L 1 и L 2 собрать схему, изображенную на рисунке 3.2а, катушки включить встречно и измерить напряжение на резисторе R 1. 3.5.6 Собрать схему, представленную на рисунке 3.3б, и измерить напряжение на вторичной обмотке трансформатора при холостом ходе и напряжение на резисторе R 1. 3.5.7 Собрать схему, изображенную на рисунке 3.3в, и измерить напряжение на вторичной обмотке нагруженного трансформатора и на резисторе R1 (для определения тока первичной обмотки нагруженного трансформатора).
Обработка результатов 3.6.1 По результатам п. 3.5.2 определить индуктивность катушки L 1 при R 1=300 Ом. Расчет произвести по формуле:
где
3.6.2 По результатам п. 3.5.3 определить индуктивность катушки L 2, используя для этого приведенное выше выражение (R 1=300 Ом). 3.6.3 По результатам п. 3.5.4 определить индуктивность согласно включенных катушек L 1 и L 2. 3.6.4 По результатам п. 3.5.3 определить индуктивность встречено включенных катушек L 1 и L 2. 3.6.5 Используя результаты пп. 3.6.3, 3.6.4, найти взаимную индуктивность М между катушками по формуле:
3.6.6 По результатам п. 3.5.6 определять ток первичной обмотки трансформатора при холостом ходе. R1=300 Ом. 3.6.7 По результатам п. 3.5.7 определить ток первичной обмотки нагруженного трансформатора. 3.6.8 Определить абсолютные и относительные погрешности измерений.
Контрольные вопросы 1. Какие цепи называют связанными? 2. Какие виды связи возможны между цепями? 3. Что такое коэффициент связи двух контуров? 4. Чему равен коэффициент связи двух контуров, связанных магнитно? 5. Какое включение двух магнитно связанных цепей называют согласным и какое встречным? 6. Как экспериментально определить взаимную индуктивность между двумя катушками? 7. Что называется воздушным трансформатором? 8. Чему равно напряжение на зажимах разомкнутой вторичной цепи воздушного трансформатора? 9. Что такое вносимое сопротивление? 10. Где целесообразно применять воздушные трансформаторы? 11. Что такое коэффициент трансформации? 12. Нарисовать схему замещения воздушного трансформатора. 13. Построить векторную диаграмму напряжений и токов для воздушного трансформатора. Рекомендуемая литература [1, c.129–146; 2, c. 103–121; 3, c. 200–213, 4, c. 242–252].
Лабораторная работа № 4
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.99.80 (0.01 с.) |



 Рисунок 3.2 – Упрощенные принципиальные схемы стенда
Рисунок 3.2 – Упрощенные принципиальные схемы стенда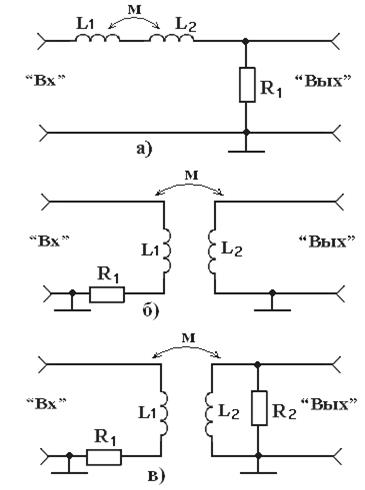


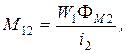 (3.1)
(3.1) (3.2)
(3.2) – число витков в первой и второй цепях;
– число витков в первой и второй цепях;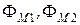 – магнитные потоки взаимной индукции первой и второй цепей соответственно;
– магнитные потоки взаимной индукции первой и второй цепей соответственно; – потокосцепление первой цепи, обусловленное током i 2 второй цепи;
– потокосцепление первой цепи, обусловленное током i 2 второй цепи; – потокосцепление второй цепи, обусловленное током i 1 первой цепи.
– потокосцепление второй цепи, обусловленное током i 1 первой цепи.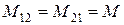 . Величина М является скалярной. Линейные индуктивно связанные цепи обладают свойством взаимности: если ток первой цепи обусловливает во второй цепи потокосцепление взаимной индукции
. Величина М является скалярной. Линейные индуктивно связанные цепи обладают свойством взаимности: если ток первой цепи обусловливает во второй цепи потокосцепление взаимной индукции  , то такой же ток, протекающий во второй цепи, обусловливает в первой цепи потокосцепление взаимной индукции
, то такой же ток, протекающий во второй цепи, обусловливает в первой цепи потокосцепление взаимной индукции 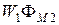 той же величины.
той же величины.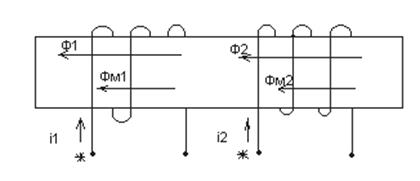
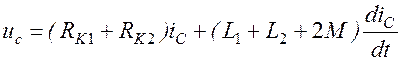 , (3.3)
, (3.3) – индуктивности первой и второй катушек;
– индуктивности первой и второй катушек; – активные сопротивления первой и второй катушек;
– активные сопротивления первой и второй катушек; – ток при согласном включении катушек.
– ток при согласном включении катушек.
 определяется в этом случае выражением:
определяется в этом случае выражением: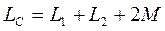 . (3.4)
. (3.4)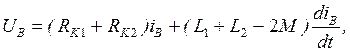 (3.5)
(3.5) – ток при встречном включении катушек.
– ток при встречном включении катушек. определяется в этом случае формулой:
определяется в этом случае формулой: . (3.6)
. (3.6)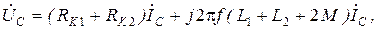 (3.7)
(3.7) . (3.8)
. (3.8)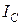 и
и  при согласном и встречном включении взаимно связанных индуктивностей, если на их вход подано напряжение
при согласном и встречном включении взаимно связанных индуктивностей, если на их вход подано напряжение  :
: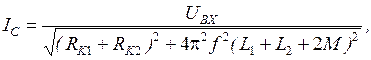 (3.9)
(3.9)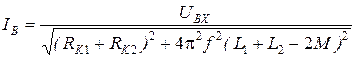 . (3.10)
. (3.10) , то выражения (3.9), (3.10) упрощаются:
, то выражения (3.9), (3.10) упрощаются: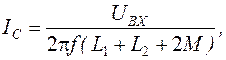 (3.11)
(3.11) . (3.12)
. (3.12)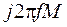 носит название сопротивление связи. Эта величина положительна при согласном включении катушек и отрицательна при встречном включении.
носит название сопротивление связи. Эта величина положительна при согласном включении катушек и отрицательна при встречном включении. . (3.13)
. (3.13) , то уравнения трансформатора запишутся в виде:
, то уравнения трансформатора запишутся в виде: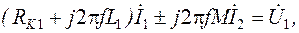 (3.14)
(3.14) . (3.15)
. (3.15)
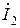 и подставляя его значение в выражение (3.14), найдем сопротивление на входе трансформатора:
и подставляя его значение в выражение (3.14), найдем сопротивление на входе трансформатора: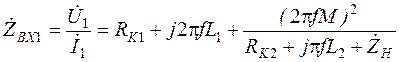 . (3.16)
. (3.16) , вносимое из вторичной обмотки в первичную:
, вносимое из вторичной обмотки в первичную: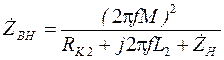 . (3.17)
. (3.17) , то выражение (3.17) запишется в виде:
, то выражение (3.17) запишется в виде: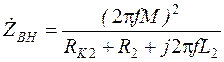 . (3.18)
. (3.18)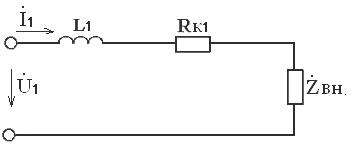
 и реактивная
и реактивная 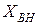 составляющие вносимого сопротивления определятся выражениями:
составляющие вносимого сопротивления определятся выражениями: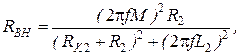 (3.19)
(3.19)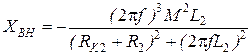 . (3.20)
. (3.20) и уравнение трансформатора записывается в виде:
и уравнение трансформатора записывается в виде: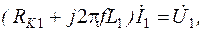 (3.21)
(3.21) . (3.22)
. (3.22)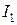 и напряжение вторичной обмотки трансформатора
и напряжение вторичной обмотки трансформатора 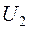 определятся в этом случае выражениями:
определятся в этом случае выражениями: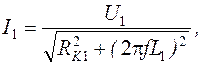 (3.23)
(3.23)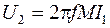 . (3.24)
. (3.24) и
и  или токов
или токов  и
и 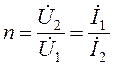 . (3.25)
. (3.25)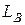 =90 мГн включения, используя выражения (3.4), (3.6).
=90 мГн включения, используя выражения (3.4), (3.6).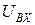 =1 В, его частота
=1 В, его частота  =10 кГц. Входным сопротивлением генератора, сопротивлением резистора и потерями в катушках индуктивности пренебречь. Для расчета воспользоваться формулами (3.11), (3.12).
=10 кГц. Входным сопротивлением генератора, сопротивлением резистора и потерями в катушках индуктивности пренебречь. Для расчета воспользоваться формулами (3.11), (3.12). ,
, 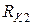 (потерями в трансформаторе), сопротивлением R1 и внутренним сопротивлением генератора пренебречь, напряжение на первичной обмотке
(потерями в трансформаторе), сопротивлением R1 и внутренним сопротивлением генератора пренебречь, напряжение на первичной обмотке  составляющие сопротивлений, вносимых из вторичной отмотки трансформатора (см. рисунок 3.3б) в первичную. Вторичная обмотка нагружена на сопротивление R 2.
составляющие сопротивлений, вносимых из вторичной отмотки трансформатора (см. рисунок 3.3б) в первичную. Вторичная обмотка нагружена на сопротивление R 2. пренебречь. Расчет произвести по формулам (3.19), (3.20).
пренебречь. Расчет произвести по формулам (3.19), (3.20).
 – напряжение на резисторе R 1,
– напряжение на резисторе R 1,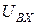 =1В;
=1В;  =10 кГц.
=10 кГц.