
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие цепи переменного токаСодержание книги
Поиск на нашем сайте
2.1 Цель работы: исследование частотных характеристик простейших цепей переменного тока.
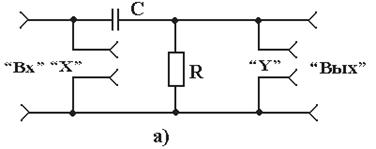
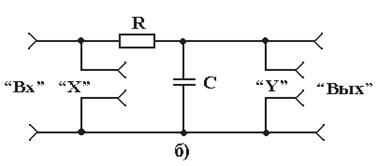
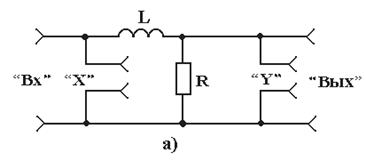
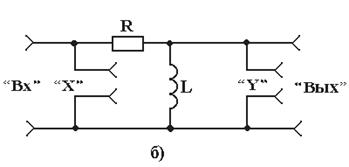
2.2 Оборудование и материалы: электрический стенд для исследования простейших цепей переменного тока, низкочастотный генератор, милливольтметр В3-33, осциллограф С1-72 или С1-73. Принципиальная электрическая схема стенда приведена на рисунке 2.1. С помощью гнезд 1-17 и электрических проводников между входом и выходом стенда обеспечивается включение цепи, состоящей из резистора R, конденсатора С или из резистора R и индуктивности L. Упрощенные принципиальные электрические схемы стенда, необхо-димые для выполнения работы, представлены на рисунках 2.2 и 2.3. Схема рисунка 2.2а получается путем соединения между собой с помощью электрических проводников гнезд 6 и 8, 7 и 9, 12 и 13; схема рисунка 2.2б – путем соединения гнезд 6 и 8, 7 и 9, 3 и 13. Для получения схем рисунка 2.3 вместо емкости С к гнездам 8, 9 подключаются выводы 10, 11 катушки индуктивности L. Схемы рисунков 2.3а и 2.3б образуются путем соединения между собой гнезд 12 и 13 в первом случае и гнезд 3 и 13 во втором. Гнезда 1, 2 (вход стенда) предназначены для подключения низкочас-тотного генератора. Напряжение на входе стенда устанавливается и кон-тролируется по измерительному прибору генератора. Гнезда 16, 17 (выход стенда) предназначены для подключения милливольтметра, а гнезда 4, 5 (“X”) и 14, 15 (“Y”) – для подключения соответственно усилителя горизонтального и вертикального отклонения осциллографа, что необходимо при измерении угла сдвига фаз между входным и выходным напряжением.
Сведения из теории Расчет простейших RL- и RC-цепей при воздействии на их входе гармонического напряжения
заключается в определении гармонического тока цепи
а также гармонических напряжений на элементах цепи R, L или R, C. В выражениях (2.1) и (2.2) приняты следующие обозначения:
Рисунок 2.1 – Принципиальная схема стенда
Рисунок 2.2 – Упрощённые принципиальные схемы стенда (RC-цепь)
Рисунок 2.3 – Упрощённые принципиальные схемы стенда (RL-цепь)
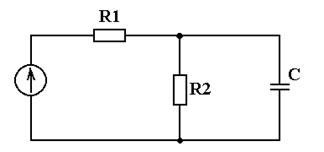
Рисунок 2.4 – Источник напряжения и параллельная RC-цепь
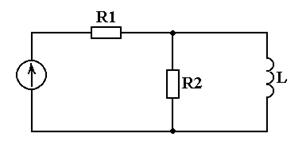
Рисунок 2.5 – Источник напряжения и параллельная RL-цепь Как видно из выражения (2.2), для определения величины гармонического тока i(t) необходимо найти его амплитуду Im или действующее значение I и фазовый сдвиг Для расчета простейших RL- и RC-цепей при воздействии на их входе гармонического напряжения, определяемого выражением (2.1), используют метод комплексных амплитуд. Суть данного метода заключается в переходе от гармонической функции u(t) к комплексной амплитуде
Комплексное сопротивление Ż -цепи в общем случае определяется выражением:
где R – активная составляющая комплексного сопротивления цепи; X –реактивная составляющая комплексного сопротивления цепи. Выражение (2.5) для комплексного сопротивления Ż может быть определено также в показательной форме:
где Z – модуль комплексного сопротивления; Величины Z и
Причем величина
Для расчета комплексного действующего значения тока в цепи используется закон Ома в комплексной форме:
Модуль I действующего комплексного значения тока İ (действующее значение тока) определяется выражением:
Подставляя вместо Z его значение из формулы (2.7), получим:
Для RC-цепи, изображенной на рисунке 2.2, комплексное сопротивление цепи ŻRC равно:
Комплексное действующее значение тока İС определяется из выражения:
Комплексные действующие значения напряжений ŬRC и ŬC на сопротивлении R и емкости C будут равны:
Фазовый сдвиг
Действующее значение тока
Для RL-цепи, изображенной на рисунке 2.3, комплексное сопротивление цепи будет равно:
Комплексные действующие значения тока İL, напряжения на сопротивлении ÚR и напряжения на индуктивности UL определяются выражениями:
Фазовый сдвиг
Действующие значения тока
Расчет участка цепи, содержащего параллельные ветви, удобно выполнять, используя понятие комплексной проводимости
где В показательной форме выражение для комплексной проводимости
где Проводимости активного сопротивления R, емкости С и индуктивности L определяются выражениями:
Комплексное сопротивление
Комплексная проводимость
Комплексное действующее значение тока
Комплексное действующее значение тока IK в к -той ветви находится по формуле:
При расчете электрической цепи со смешанным соединением элементов (рисунка 2.4, 2.5) вначале находят эквивалентную комплексную проводимость
После этого находят комплексное сопротивление Ż ветвей цепи, суммируя
Например, для цепи, изображенной на рисунке 2.4, значение
Тогда величина
Значение
Подготовка к лабораторной работе 2.4.1 Рассчитать зависимость действующего значения тока от частоты f в цепи, состоящей из последовательно соединенных сопротивления R и емкости С. Действующее значение напряжения, приложенного к цепи, U =1 В. Величина R =1 кОм, С =0,1 мкФ. Расчет произвести для частот 50, 100, 200, 400, 800, 1600, 3200, 6400, 12800, 25600, 51200 Гц с помощью программируемого микрокалькулятора на основании выражения (2.19). Программы расчета с помощью программируемого микрокалькулятора «Электроника Б3-34» приведены в Приложении А. 2.4.2 Используя данные п. 2.1.1, рассчитать зависимость от частоты угла сдвига фаз между током и приложенным к цепи напряжением по формуле (2.18).Программы расчета на микрокалькуляторе «Электроника Б3-34» представлены в Приложении А. 2.4.3 Используя данные п. 2.4.1, рассчитать зависимость напряжения Uc на емкости от частоты на основании выражения (2.21). Программы расчета на микрокалькуляторе «Электроника Б3-34» приведены в Приложении 1. 2.4.4 По результатам пп.2.4.1, 2.4.2, 2.4.3 построить на одном чертеже графики, используя для оси частот f логарифмический масштаб
2.4.5 Рассчитать зависимость тока от частоты f в цепи, состоящей из последовательно соединенных сопротивлений R и индуктивности L. Действующее значение напряжения, приложенного к цепи, – 1 В. Величина R =1 кОм, L =0,05 Гн. Расчет произвести с помощью программируемого микрокалькулятора по формуле (2.27) для тех же частот, что и в п. 2.4.1. 2.4.6 Используя данные п. 2.4.5, рассчитать зависимость от частоты сдвига фаз между током и приложенным к цепи напряжением. Расчет произвести с помощью программируемого микрокалькулятора по формуле (2.26). 2.4.7 Используя данные п. 2.4.5, рассчитать зависимость напряжения 2.4.8 По результатам пп. 2.4.5–2.4.7 построить на одном чертеже графики, используя для оси частот логарифмический масштаб.
Порядок выполнения работы 2.5.1 Собрать схему, представленную на рисунке 2.2а. 2.5.2 Установить действующее значение напряжения на входе стенда 1 В, используя для этого измерительный прибор генератора. При всех последующих измерениях напряжение на входе стенда должно быть равно 1 В. 2.5.3 Снять зависимость напряжения на сопротивлении R от частоты для значений частот, указанных в подразделе 2.4 (во всех пунктах лабораторного задания измерения проводить на этих частотах). 2.5.4 Снять зависимость угла сдвига фаз между током в RC -цепи и входным напряжением от частоты, учитывая, что напряжение на сопротивлении R совпадает по фазе с током, протекающим через него. Методика измерения угла сдвига фаз приведена в Приложении Б. 2.5.5 Собрать схему, изображенную не рисунке 2.2б, и снять зависимость напряжения на конденсаторе С от частоты. 2.5.6 Собрать схему, представленную на рисунке 2.3а, и снять зависимость напряжения на сопротивлении R от частоты. 2.5.7 Снять зависимость угла сдвига фаз между током в RL -цепи и входным напряжением, используя методику Приложения Б. 2.5.8 Собрать схему, изображенную на рисунке 2.3б, и снять зависимость напряжения на катушке индуктивности L от частоты. Обработка результатов 2.6.1 По данным п. 2.5.3 рассчитать зависимость тока в RС- цепи от частоты. 2.6.2 По данным пп. 2.5.1, 2.5.4, 2.5.5 построить на одном чертеже графики, используя тот же масштаб, что и в п. 2.4.4. 2.6.3 По данным п. 2.5.6 рассчитать зависимость тока в RL- цепи от частоты. 2.6.4 По данным пп. 2.5.3, 2.5.7 и 2.5.6 построить на одном чертеже графики, используя тот же масштаб, что и в п. 2.4.8.
2.6.5 Вычислить для каждой полученной зависимости максимальное отклонение результатов, полученных экспериментально, от расчетных.
Контрольные вопросы 1. Как изменяется ток в цепи, состоящей из последовательно соединённых емкости и сопротивления, при изменении частоты приложенного к цепи гармонического напряжения постоянной амплитуды? 2. Как изменяется ток в цепи, состоящей из последовательно соединённых сопротивления и индуктивности, при изменении частоты приложенного к цепи гармонического напряжения постоянной амплитуды? 3. Как изменяется ток источника гармонической ЭДС постоянной амплитуды, к которому подключена цепь, состоящая из параллельно соединенных емкости и сопротивления, при изменении частоты ЭДС? 4. Как изменяется ток источника гармонической ЭДС постоянной амплитуды, к которому подключена цепь, состоящая из параллельно соединенных индуктивности и сопротивления, при изменении частоты ЭДС? 5. Как зависит от частоты угол сдвига фаз между током источника гармонической ЭДС и его напряжением, если нагрузкой являются последовательно соединенные емкость и активное сопротивление? 6. Как зависит от частоты угол сдвига фаз между током источника гармонической ЭДС и его напряжением, если нагрузкой являются параллельно соединенные емкость и активное сопротивление? 7. Как зависит от частоты угол сдвига фаз между током источника гармонической ЭДС и его напряжением, если нагрузкой являются последовательно соединенные индуктивность и активное сопротивление? 8. Как зависит от частоты угол сдвига фаз между током источника гармонической ЭДС и его напряжением, если нагрузкой являются параллельно соединенные индуктивность и активное сопротивление? 9. Как зависит от частоты напряжение на сопротивлении цепи, изображенной на рисунке 1.4? 10. Как зависит от частоты напряжение на сопротивлении цепи, изображенной на рисунке 1.5?
Рекомендуемая литература: [1, с. 63-96; 2, с. 28-47; 3, с. 50-89; 4, с. 191-202].
Лабораторная работа № 3
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.182 (0.009 с.) |

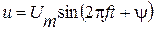 (2.1)
(2.1)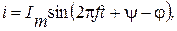 (2.2)
(2.2)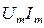 – амплитудные значения гармонического напряжения и тока соответственно; f – частота изменения гармонического напряжения и тока;
– амплитудные значения гармонического напряжения и тока соответственно; f – частота изменения гармонического напряжения и тока; 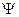 – начальная фаза гармонического напряжения.
– начальная фаза гармонического напряжения.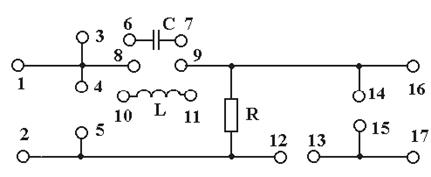
 .
.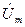 или комплексному действующему значению
или комплексному действующему значению 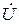 , в определении комплексного сопротивления цепи Ż и нахождении комплексной амплитуды тока İm или комплексного действующего значения İ. Затем осуществляется переход от комплексного амплитудного или действующего значения тока к его мгновенному значению, определяемому выражением (2.2). Комплексные амплитудное
, в определении комплексного сопротивления цепи Ż и нахождении комплексной амплитуды тока İm или комплексного действующего значения İ. Затем осуществляется переход от комплексного амплитудного или действующего значения тока к его мгновенному значению, определяемому выражением (2.2). Комплексные амплитудное 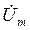 и действующее
и действующее 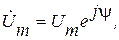 (2.3)
(2.3)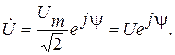 (2.4)
(2.4)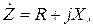 (2.5)
(2.5)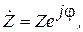 (2.6)
(2.6)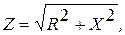 (2.7)
(2.7)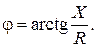 (2.8)
(2.8)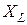 и емкости
и емкости 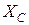 :
: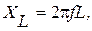 (2.9)
(2.9)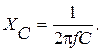 (2.10)
(2.10)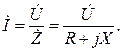 (2.11)
(2.11)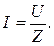 (2.12)
(2.12)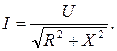 (2.13)
(2.13)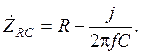 (2.14)
(2.14)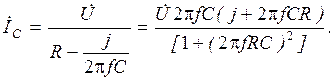 (2.15)
(2.15)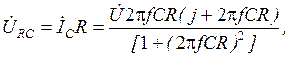 (2.16)
(2.16)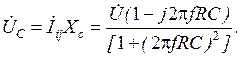 (2.17)
(2.17)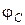 определяется выражением:
определяется выражением: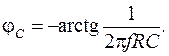 (2.18)
(2.18)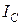 , напряжение на сопротивлении
, напряжение на сопротивлении 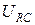 и напряжение на емкости
и напряжение на емкости 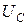 , представляющие собой модули выражений (2.15–2.17), запишутся в виде:
, представляющие собой модули выражений (2.15–2.17), запишутся в виде: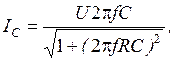 (2.19)
(2.19)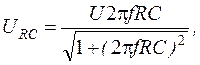 (2.20)
(2.20)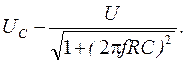 (2.21)
(2.21)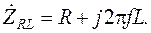 (2.22)
(2.22)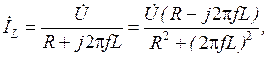 (2.23)
(2.23)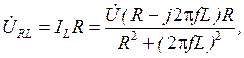 (2.24)
(2.24)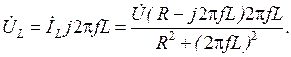 (2.25)
(2.25)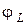 будет равен:
будет равен: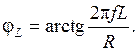 (2.26)
(2.26)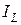 , напряжения на сопротивлении
, напряжения на сопротивлении 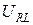 и напряжения на индуктивности
и напряжения на индуктивности 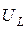 , определяемые из выражений (2.23)–(2.25), будут иметь вид:
, определяемые из выражений (2.23)–(2.25), будут иметь вид: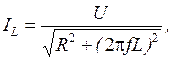 (2.27)
(2.27)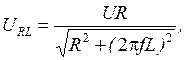 (2.28)
(2.28)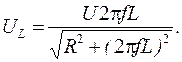 (2.29)
(2.29)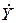 :
: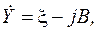 (2.30)
(2.30)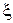 – активная составляющая комплексной проводимости; B – реактивная составляющая комплексной проводимости.
– активная составляющая комплексной проводимости; B – реактивная составляющая комплексной проводимости.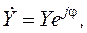 (2.31)
(2.31)
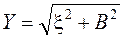 – модуль комплексной проводимости;
– модуль комплексной проводимости; 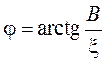 – аргумент вектора
– аргумент вектора  .
. (2.32)
(2.32)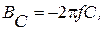 (2.33)
(2.33)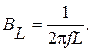 (2.34)
(2.34)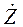 и проводимость
и проводимость 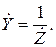 (2.35)
(2.35)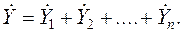 (2.36)
(2.36)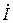 в неразветвленной цепи с напряжением
в неразветвленной цепи с напряжением 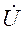 на ее входе определяется выражением:
на ее входе определяется выражением: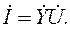 (2.37)
(2.37)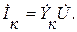 (2.38)
(2.38)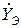 параллельно соединенных ветвей, затем определяют соответствующее ей эквивалентное комплексное сопротивление
параллельно соединенных ветвей, затем определяют соответствующее ей эквивалентное комплексное сопротивление 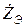 :
: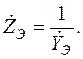 (2.39)
(2.39)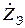 и комплексное сопротивление
и комплексное сопротивление 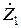 последовательно соединенных ветвей:
последовательно соединенных ветвей: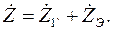 (2.40)
(2.40)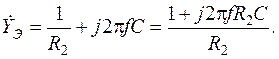 (2.41)
(2.41)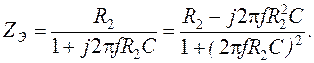 (2.42)
(2.42)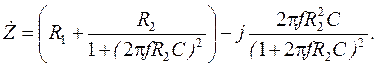 (2.43)
(2.43)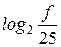 . Так как
. Так как 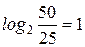 ,
, 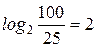 и т.д., то заданным частотам будут соответствовать точки на оси абсцисс со значениями 1, 2, 3, ……, 11.
и т.д., то заданным частотам будут соответствовать точки на оси абсцисс со значениями 1, 2, 3, ……, 11.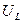 на индуктивности от частоты на основании выражения (2.29). Программы расчета на микрокалькуляторе «Электроника Б3-34» приведены в Приложении А.
на индуктивности от частоты на основании выражения (2.29). Программы расчета на микрокалькуляторе «Электроника Б3-34» приведены в Приложении А.


