
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование разветвленной электрической цепи с одним источником постоянного токаСодержание книги
Поиск на нашем сайте
10.1 Цель работы: освоение методов эквивалентного преобразования электрической цепи; проведение опытной проверки аналитического расчета цепи с использованием законов Ома и Кирхгофа и подтверждение в их справедливости.
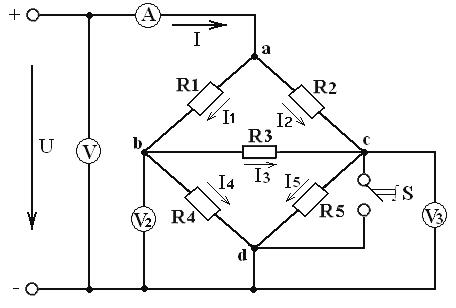
10.2 Оборудование и материалы: стенд, оборудованный источниками постоянного и переменного токов, щитовыми электроизмерительными приборами, наборами резисторов, конденсаторов и ключей, гнездами, сигнальными лампочками. Электропитание стенда осуществляется от силового щита лаборатории, содержащего разделительный трансформатор, коммутационную аппаратуру, устройства защиты и световой сигнализации. Конкретная схема исследуемой цепи собирается с помощью проводников, элементов и приборов стенда. При этом необходимо помнить о соблюдении полярности подключения амперметров и вольтметров постоянного тока и правильном выборе пределов измерения приборов. Принципиальная электрическая схема исследуемой цепи представлена на рисунке 10.1.
Рисунок 10.1 – Электрическая схема разветвлённой цепи постоянного тока
Сведения из теории Расчет линейных разветвленных электрических цепей с одним источником постоянного тока проводят с использованием законов Ома и Кирхгофа. Эквивалентное сопротивление цепи R Э с входным током I при подключении к её входу напряжения U определяется законом Ома:
Применяя первый закон Кирхгофа для узлов разветвления цепи, а второй закон Кирхгофа для отдельных контуров разветвленной цепи (при известных величинах I, U и сопротивлений ветвей R i) находят токи, напряжения, мощности на отдельных участках. До записи уравнений по законам Кирхгофа на схеме цепи стрелкой указывают условно положительные направления токов в ветвях. Эти условно положительные направления токов выбирают произвольно. Первый закон Кирхгофа: алгебраическая сумма токов в узле разветвления равна нулю. Физически первый закон Кирхгофа выражает закон сохранения заряда. Если с узлом исследуемой цепи соединено n ветвей, то уравнение по первому закону Кирхгофа для него будет иметь вид:
При этом втекающие в узел токи выбирают со знаком «плюс», а токи, вытекающие из узла, – со знаком «минус». (Допускается использование и обратного правила выбора знаков токов). При расчёте цепи уравнения по первому закону Кирхгофа записываются только для независимых узлов. Их число всегда на 1 меньше общего количества узлов. Например, если электрическая цепь имеет q узлов, то число независимых узлов будет равно q -1. Второй закон Кирхгофа: при обходе контура электрической цепи в любом направлении алгебраическая сумма падений напряжений на электрических элементах контура (сопротивлениях, индуктивностях, ёмкостях) равна алгебраической сумме действующих в контуре э.д.с. Направление обхода контура выбирается произвольно и указывается внутри контура стрелкой. Если контур содержит l источников э.д.с. и k электрических элементов, то уравнение по второму закону Кирхгофа запишется для него в виде:
В уравнениях по второму закону Кирхгофа напряжения на элементах и э.д.с. источников выбираются со знаком «плюс», если их положительно выбранные направления совпадают с направлением обхода контура. В противном случае их величины берутся со знаком «минус». Уравнение второго закона Кирхгофа для контура, не содержащего источников э.д.с., запишется в виде:
Число расчетных уравнений по второму закону Кирхгофа определяется количеством независимых контуров n, которое рассчитывается по числу ветвей р и числу узлов q схемы цепи:
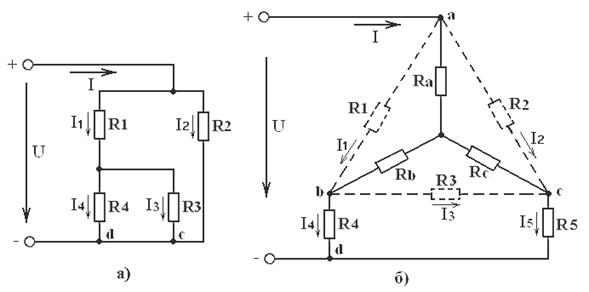
Решив совместно уравнения, составленные по законам Кирхгофа, определяют токи в отдельных ветвях. Если при решении получится отрицательное значение тока той или иной ветви, то этот ток имеет направление, обратное указанному на схеме. Наряду с методом, основанным на использовании законов Кирхгофа, для расчёта разветвлённой электрической цепи используют метод эквивалентных преобразований. По этому методу всю схему разбивают на отдельные участки, содержащие только последовательно соединённые или только параллельно соединённые элементы. Находят эквивалентные сопротивления таких участков и, учитывая способ соединения их между собой, эквивалентное сопротивление всей цепи и её ток. Далее, используя закон Ома, находят необходимые напряжения между узлами и токи ветвей. В методе эквивалентных преобразований схема исходной разветвлённой электрической цепи заменяется более простыми схемами цепей, которые имеют такое же эквивалентное сопротивление. Если схема разветвлённой цепи содержит участки, в которых элементы соединены по схеме «Звезда» (сопротивления R a, R b, R c рисунка 10.2а) или «Треугольник» (сопротивления R 1, R 2, R 3 рисунка 10.2б), то для расчёта эквивалентного сопротивления цепи преобразуют «Звезду» в «Треугольник» или наоборот. Эквивалентным преобразованием «Треугольника» в «Звезду» называется такая замена части цепи, соединённой по схеме «Треугольник», цепью, соединённой по схеме «Звезда», при которой токи и напряжения в остальной части цепи остаются неизменными. Иначе говоря, при одинаковых напряжениях между одноимёнными узлами входящие в них токи одинаковы и для «Треугольника», и для «Звезды». То есть мощности в этих цепях одинаковы. Преобразование «Треугольника» в «Звезду» производится по формулам:
Рисунок 10.2 – Схемы соединения сопротивлений: а) «Звездой»; б) «Треугольником»
Обратное преобразование «Звезды» в «Треугольник» осуществляется с использованием выражений:
В настоящей работе с помощью ключа S можно менять конфигурацию исследуемой цепи, приведенной на рисунке 10.1. При замкнутом положении ключа S точки c и d схемы соединяются между собой, в результате чего резистор R 5 шунтируется проводником, и цепь может быть представлена в виде, изображенном на рисунке 10.3а.
Рисунок 10.3 – Эквивалентные схемы исследуемых цепей: а) ключ S замкнут; б) ключ S разомкнут Как видно из рисунка, цепь состоит из ветви R 2 и последовательно-параллельного соединения сопротивлений R 1, R 3 и R 4. Учитывая, что эквивалентное сопротивление R Э1 последовательно-параллельной ветви данной цепи равно:
выражение для общего эквивалентного сопротивления цепи R Э будет иметь вид:
Тогда токи I, I 1, I 2 найдём по закону Ома:
Ток I 1 в ветвях R 3 и R 4 распределится обратно пропорционально величинам этих сопротивлений, поэтому ток I 3, можно определить по формуле:
Ток I 4 найдём по первому закону Кирхгофа для узла «b»:
При оформлении отчета по данной работе необходимо величины токов, вычисленные аналитически по приведенной выше методике, сравнить с токами тех же участков, определяемых по данным измерений, а именно:
Уравнения При разомкнутом положение ключа S электрическая цепь представляется в виде, приведенном на рисунке 10.3б. Эквивалентное сопротивление этой цепи может быть найдено путём предварительного преобразования «Треугольника» в «Звезду». В рассматриваемой электрической цепи наиболее целесообразно преобразовать треугольник резисторов R 1, R 2, R 3 в эквивалентную звезду по формулам (10.5). Цепь после преобразования схемы цепи будет иметь вид, показанный на рисунке 10.3б сплошными линиями. Входной ток преобразованной цепи и токи в её ветвях находят в следующем порядке. По закону Ома определяют входной ток:
Токи в параллельных ветвях распределятся обратно пропорционально их сопротивлениям:
Токи I 1, I 2, I 3 в ветвях с резисторами R 1, R 2, R 3 можно определить, используя второй закон Кирхгоффа:
Токи I, I 1÷ I 5, полученные расчетным путем, необходимо сравнить с токами, найденными по данным измерений потенциалов в экспериментальной части работы.
где U 2 и U 3 – напряжения на резисторах R 4 и R 5 соответственно. Направление токов определяется по знаку результата вычислений.
Подготовка к работе 10.4.1 Получить у преподавателя значения сопротивлений R 1 – R 5 для расчёта схемы рисунка 10.1 и занести их в таблицу 10.2. 10.4.2 Используя формулы 10.6 – 10.10 рассчитать эквивалентное сопротивление цепи R Э, входной ток цепи I, токи I 1 – I 4 ветвей при замкнутом ключе S. Входное напряжение цепи U = 30 В. Полученные расчёты занести в таблицу 10.1.
Таблица 10.1 – Результаты расчетов
10.4.3 Используя формулы 10.12 – 10.17, рассчитать эквивалентное сопротивление цепи R Э, входной ток цепи I, токи I 1 – I 5 ветвей при разомкнутом ключе S. Входное напряжение цепи U = 30 В. Полученные расчёты занести в таблицу 10.1.
Порядок выполнения работы 10.5.1 Ознакомиться с приборами и элементами экспериментальной установки и записать их технические характеристики в журнал лабораторных работ. 10.5.2 Собрать электрическую цепь по схеме, приведенной на рисунке 10.1. 10.5.3 После проверки руководителем правильности соединений приборов и элементов установки подключить к её входу источник питания и замкнуть ключ S. Вольтметрами V, V 2, V 3 измерить напряжения на входе цепи U и напряжения U 2, U 3 между узлами b и d, c и d соответственно, принимая точку «d» за общую точку схемы (точку нулевого потенциала). 10.5.4 Повторить п.10.5.3 при разомкнутом ключе S. Результаты экспериментальных измерений при замкнутом и разомкнутом ключе S занести в таблицу 10.2.
Таблица 10.2 – Результаты экспериментальных измерений
Обработка результатов 10.6.1 На основе экспериментальных данных, полученных в п.10.5.3, определить с помощью формул (10.11) величины токов в ветвях при замкнутом ключе S. Результаты расчетов занести в таблицу 10.1. 10.6.2 С помощью экспериментальных данных, полученных в п. 10.5.5, найти с помощью формул (10.18) величины токов в ветвях при разомкнутом положении ключа S. Результаты расчетов занести в таблицу 10.1. 10.6.3 Сравнить величины токов в ветвях, вычисленные аналитически, с токами тех же ветвей, полученными экспериментальным путём. Рассчитать погрешности измерений. 10.6.4 Сделать выводы по работе, оформить отчёт о выполнении лабораторной работы, подготовиться к его защите.
10.7 Контрольные вопросы: 1. Объяснить порядок выполнения работы. 2. Что такое электрическая цепь, элемент цепи? 3. Какие электрические элементы цепи вы знаете? 4. Чем различаются активные и пассивные элементы электрической цепи? 5. Чем отличается источник э.д.с. (напряжения) от источника тока? 6. Что называется схемой электрической цепи? 7. Назовите геометрические элементы схемы электрической цепи. 8. Что такое ветвь, узел? 9. Что такое контур? 10. Сформулируйте закон Ома, запишите его математически. 11. Сформулируйте первый закон Кирхгофа. Что он выражает физически? 12. Сформулируйте второй закон Кирхгофа. Поясните его физический смысл. 13. Как записывают математически законы Кирхгофа? 14. Как выбираются положительные направления токов, напряжений и э.д.с. источников напряжения при записи уравнений по законам Кирхгофа? 15. Как экспериментально определить величину сопротивления участка электрической цепи? 16. Какие цепи называются эквивалентными? 17. Чему равно эквивалентное сопротивление цепи при последовательном, параллельном и смешанном соединении элементов? 18. Какое соединение элементов называется «Звездой»? «Треугольником»? 19. В чём заключается условие эквивалентности преобразования «Звезды» в «Треугольник»? 20. Записать формулы, с помощью которых осуществляется преобразование «Звезды» в «Треугольник». 21. Записать формулы, с помощью которых осуществляется преобразование «Треугольника» в «Звезду». 22. Что такое класс точности прибора? 23. Что такое абсолютная, относительная и приведённая погрешности измерения? 24. Измерительные приборы какой системы использовались при выполнении работы?
Рекомендуемая литература [1; с.7 – 49; 5; с.5–12, 14–20, 25–44]. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Основная литература 1. Попов, В.П. Основы теории цепей [Текст]: учеб. пособие для вузов / В.П. Попов. – 4 изд., испр. – М.: Высшая школа, 2003. – 576 с.: ил. 2. Атабеков, Г.И. Основы теории электрических цепей [Текст] / Г.И. Атабеков. – М.: Энергия, 1969. – 763 с.: ил. 3. Атабеков, Г.И. Теоретические основы электротехники [Текст] / Г.И. Атабеков. – М.: Энергия, 1978. – 592 с.: ил.
Дополнительная литература 4. Демирчян, К.С. Теоретические основы электротехники [Текст]: учебник для вузов / К.С. Демирчян [и др.]. – СПб.: Энергия, 2003. – 1416 с.: ил. 5. Касаткин, А.С. Электротехника [Текст]: учебник для вузов / А.С. Ка-саткин, М.В. Немцов. – 6 изд., перераб. – М.: Высш. шк., 2000. – 544 с.: ил.
ПРИЛОЖЕНИЕ А (рекомендуемое)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.80.88 (0.007 с.) |

 . (10.1)
. (10.1)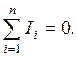 (10.2)
(10.2)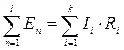 . (10.3)
. (10.3) .
.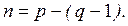 (10.4)
(10.4)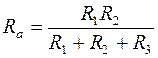 ;
; 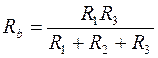 ;
;  . (10.5)
. (10.5)


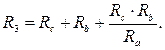
 , (10.6)
, (10.6) . (10.7)
. (10.7)
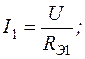
 (10.8)
(10.8)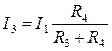 . (10.9)
. (10.9) (10.10)
(10.10)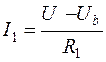 ;
;  ;
; 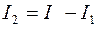 ;
; ; (10.11)
; (10.11) , для узла «a» и
, для узла «a» и  для узла «b» убеждают нас в справедливости первого закона Кирхгофа.
для узла «b» убеждают нас в справедливости первого закона Кирхгофа. ;
;  . (10.12)
. (10.12)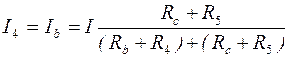 , (10.13)
, (10.13)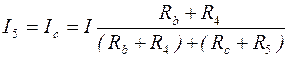 . (10.14)
. (10.14)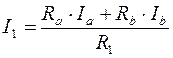 (контур R 1- R a- R b); (10.15)
(контур R 1- R a- R b); (10.15)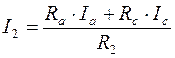 (контур R 2- R a- R с); (10.16)
(контур R 2- R a- R с); (10.16) (контур R 3- R b- R с). (10.17)
(контур R 3- R b- R с). (10.17)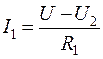 ;
; 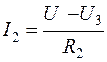 ;
; 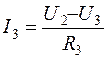 ;
;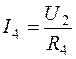 ;
;  , (10.18)
, (10.18)


