
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепь синусоидального тока с индуктивным элементомСодержание книги
Поиск на нашем сайте
В этом случае Закон Ома для индуктивности
где Пусть в цепи (рис. 3.14, а) протекает гармонический ток (рис. 3.14, б),
Рис. 3.14. Схема (а) и графики (б) напряжения тока катушки индуктивности Подставляем (3.23) в (3.22) и преобразуя в синусоидальную форму получим:
где: · · · · Напряжение на индуктивности
Рис. 3.15. Векторные диаграммы напряжения и тока для R (a), L (б) и С (в)
и в действующих значениях
Среднее значение мощности за целое число периодов равно нулю. Реактивная индуктивная мощность равна амплитуде мгновенной мощности и может быть описана формулами:
Рассмотрим частотные свойства катушки индуктивности. Из полученной формулы Рис. 3.16. График зависимости Из графика видно, что на очень высоких частотах сопротивление катушки велико и ток через катушку будет очень мал. Это свойство катушки индуктивности часто используется при построении следующей простой измерительной цепи. Катушку индуктивности одним выводом подключают к некоторой (контрольной) точке схемы. К другому выводу катушки подключают измеритель постоянного напряжения (вольтметр). Так как сопротивление катушки для постоянного тока практически равно нулю, то через такую катушку индуктивности легко измерить постоянное напряжение в контрольной точке. При этом имеющееся в этой контрольной точке высокочастотное напряжение из-за большого сопротивления катушки, во-первых, не будет изменяться и, во-вторых, не будет мешать процессу измерения, не попадая на вольтметр. В схемотехнике катушку индуктивности (дроссель) используют в виде коллекторной нагрузки на транзистор (в усилителях мощностей, генераторах, и т.д.), при этом по переменному току на катушке выделяется полезное напряжение, Пример 3.8. К индуктивному элементу Решение. Действующее значение напряжения
Комплексное напряжение
Индуктивное сопротивление
Индуктивное сопротивление в комплексной форме
Ток в индуктивном элементе
Его мгновенное значение
Мгновенное значение ЭДС индукции
или в комплексной форме: Векторная диаграмма изображена на рис. 3.17. Рис. 3.17. Векторная диаграмма к примеру 3.8
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.006 с.) |

 сопротивление цепи носит индуктивный характер.
сопротивление цепи носит индуктивный характер.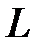 (1.7) преобразуем в комплексный вид:
(1.7) преобразуем в комплексный вид: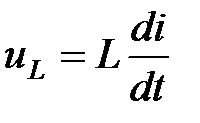 ≓
≓  (3.22)
(3.22) — реактивное индуктивное сопротивление, отражающее способность реальных объектов (например двигатели, катушки индуктивности, фильтры и т.д.) накапливать электромагнитную энергию при прохождении тока
— реактивное индуктивное сопротивление, отражающее способность реальных объектов (например двигатели, катушки индуктивности, фильтры и т.д.) накапливать электромагнитную энергию при прохождении тока  , которую оценивают в омах (Ом). Выражение (3.22) представляет собой закон Ома
, которую оценивают в омах (Ом). Выражение (3.22) представляет собой закон Ома 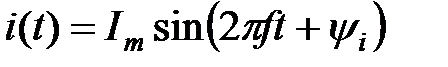 ≓
≓  (3.23)
(3.23)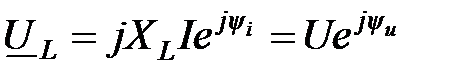 ≓
≓ 
 — действующее значение напряжения;
— действующее значение напряжения; — амплитудное значение напряжения;
— амплитудное значение напряжения; — номинальная фаза напряжения;
— номинальная фаза напряжения; — угловая частота.
— угловая частота. опережает по фазе ток на
опережает по фазе ток на  .
.  Мгновенное значение мощности будет
Мгновенное значение мощности будет ,
,
 .
. (3.24)
(3.24) следует, что сопротивление катушки увеличивается с ростом частоты. Нулевой частоте
следует, что сопротивление катушки увеличивается с ростом частоты. Нулевой частоте  соответствует постоянный ток, и в этом случае
соответствует постоянный ток, и в этом случае  . График зависимости
. График зависимости 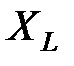 от частоты
от частоты  приведен на рис. 3.16.
приведен на рис. 3.16.
 мГн приложено синусоидальное напряжение
мГн приложено синусоидальное напряжение  В. Найти действующее значение тока, записать его мгновенное значение и мгновенное значение ЭДС самоиндукции. Построить на комплексной плоскости векторы
В. Найти действующее значение тока, записать его мгновенное значение и мгновенное значение ЭДС самоиндукции. Построить на комплексной плоскости векторы 
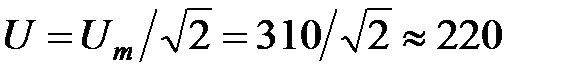 В.
В. В.
В. Ом.
Ом. Ом.
Ом.
 А.
А. B.
B. B.
B.


