
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание классического метода расчета параметров переходных процессов в электрических цепяхСодержание книги
Поиск на нашем сайте
Название метода «классический» отражает использование в нём решений дифференциальных уравнений с постоянными параметрами методами классической математики. Эти уравнения составляют для схем, полученных после коммутации, основываясь на известных методах расчета электрических цепей, таких как метод непосредственного применения законов Кирхгофа, метод контурных токов, метод узловых потенциалов. Решение полученной системы уравнений относительно выбранной переменной и составляет сущность классического метода. После того, как получили дифференциальное уравнение относительно одной переменной, следует составить общее решение полученного неоднородного дифференциального уравнения, которое записывается в виде суммы принужденной и свободной составляющих, которая описывает процесс в цепи без источников ЭДС и тока:
Здесь: 1. Хпр описывает установившиеся (принужденные процессы), определяемые внешним воздействием. По существу, это значение конечных условий при 2. 3. Но характеристическое уравнение можно получить, не составляя дифференциального уравнения цепи. Комбинированный метод в том и заключается, что характеристическое уравнение, из которого находятся корни
То есть в цепи будут протекать переходные процессы с нулевыми начальными условиями. В момент включения постоянного напряжения источника Е (при Когда начальные условия ненулевые, напряжение на емкости до начала коммутации и после не равно нулю, а ток в индуктивности до и после коммутации так же не равен нулю:
Поэтому до начала коммутации (при Данный метод применяют для решения дифференциальных уравнений первого и второго порядка. При более высоких порядках определение постоянных интегрирования и решение характеристического уравнения представляет собой сложный процесс, поэтому в сложных цепях используется операторный метод.
РАССЧЕТ ПАРАМЕТРОВ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С ДВУМЯ РЕАКТИВНЫМИ ЭЛЕМЕНТАМИ Определение основных параметров электрической цепи в начале переходного режима и в принужденном режиме В приведенной схеме, представленной на рисунке 1, были определены начальные и конечные условия для всех токов и напряжений в цепи с нулевыми начальными условиями.
Рисунок 1. Исходная схема для расчета параметров переходного процесса В таблицу 1 занесены данные для последующий расчётов: Таблица 1. Данные для расчета
В представленной схеме ненулевые начальные условия, а, следовательно, согласно законам коммутации:
1) Начальные условия ( До начала коммутации (при
Рисунок 2. Эквивалентная схема цепи для времени Ток
Напряжение на индуктивности
Контроль вычислений.
Ток 2) После коммутации (
Индуктивность в эквивалентной схеме для момента времени Так как
Рисунок 3. Эквивалентная схема цепи для времени
Для рассматриваемой схемы ГНУ:
По 1-ому закону Кирхгофа:
Отсюда следует, что:
Так как на L1 обрыв:
Напряжение на индуктивности
Контроль вычислений.
1-й и 2-й законы Кирхгофа выполняются. 3) Конечные условия ( После окончания переходного процесса все токи и напряжения в схеме (рисунок 4) будут постоянными. Так как
Рисунок 4. Эквивалентная схема цепи для времени Анализ эквивалентной схемы позволил определить токи и напряжения:
Контроль вычислений.
Таблица 2. Результаты вычислений
С учетом НУ и КУ можно качественно построить графики (рисунок 5).
Рисунок 5. Качественные графики
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.006 с.) |


 , найденных при
, найденных при 
 и
и  – постоянные интегрирования, определяемые из начальных условий, при
– постоянные интегрирования, определяемые из начальных условий, при 
 и
и  – корни характеристического уравнения, полученного из однородного дифференциального уравнения для
– корни характеристического уравнения, полученного из однородного дифференциального уравнения для  :
: 
 , где
, где 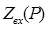 – входное операторное сопротивление цепи. Также при расчете переходных процессов в электрических цепях необходимо определить начальные и конечные условия. Когда начальные условия нулевые, напряжение на емкости до начала коммутации и после нее равно нулю, а ток в индуктивности до и после коммутации также равен нулю, согласно законам коммутации:
– входное операторное сопротивление цепи. Также при расчете переходных процессов в электрических цепях необходимо определить начальные и конечные условия. Когда начальные условия нулевые, напряжение на емкости до начала коммутации и после нее равно нулю, а ток в индуктивности до и после коммутации также равен нулю, согласно законам коммутации:

 ) напряжение
) напряжение  и ток
и ток  измениться не могут и равны нулю. Остальные величины (
измениться не могут и равны нулю. Остальные величины (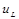 ,
,  ,
,  ,
,  ) могут измениться скачком. Следовательно, емкость в эквивалентной схеме для
) могут измениться скачком. Следовательно, емкость в эквивалентной схеме для 

 ) токи и напряжения в ветвях не будут равны нулю. Так как напряжение на емкости и ток в индуктивности изменяться скачком не могут, то емкость в эквивалентной схеме для
) токи и напряжения в ветвях не будут равны нулю. Так как напряжение на емкости и ток в индуктивности изменяться скачком не могут, то емкость в эквивалентной схеме для  , а индуктивность источником тока
, а индуктивность источником тока 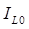 . Анализ эквивалентной схемы необходимо проводить, используя законы Ома и Кирхгофа. Значения искомых величин (токов и напряжений) нужно записать в общем виде (через Е,
. Анализ эквивалентной схемы необходимо проводить, используя законы Ома и Кирхгофа. Значения искомых величин (токов и напряжений) нужно записать в общем виде (через Е, 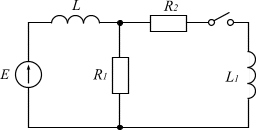


 )
)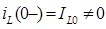 . Определим этот ток из эквивалентной схемы для
. Определим этот ток из эквивалентной схемы для 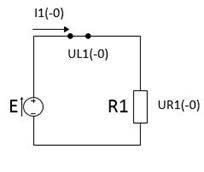
 равен (по закону Ома):
равен (по закону Ома):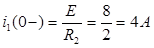 .
. , а напряжение на сопротивлении R1 равно
, а напряжение на сопротивлении R1 равно
 – второй закон Кирхгофа выполняется.
– второй закон Кирхгофа выполняется.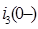 и напряжение
и напряжение 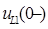 равны нулю, так как цепь R2L1 до начала коммутации отключена.
равны нулю, так как цепь R2L1 до начала коммутации отключена. .
.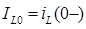 .
. , то индуктивность в эквивалентной схеме заменяется разрывом (рисунок 3).
, то индуктивность в эквивалентной схеме заменяется разрывом (рисунок 3).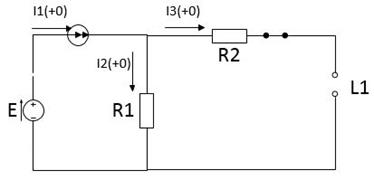

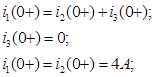


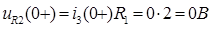

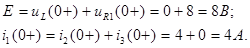
 )
) , то индуктивность в эквивалентной схеме заменяется перемычкой:
, то индуктивность в эквивалентной схеме заменяется перемычкой:

 – 1-й закон Кирхгофа выполняется.
– 1-й закон Кирхгофа выполняется.



