Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение характеристик переходных процессов классическим методомСодержание книги
Поиск на нашем сайте
Для составления дифференциального уравнения был выбран ток
Принужденная составляющая тока
Для определения корней характеристического уравнения
Рисунок 6. Эквивалентная операторная схема цепи Далее было найдено операторное входное сопротивление и приравнено к нулю (
Условие
Корни этого уравнения:
Подставив значения
После этого были определены произвольные постоянные
Откуда было получено первое уравнение для нахождения произвольных постоянных:
Для получения второго уравнения было найдено значение
Откуда получается, что второе уравнение для нахождения произвольных постоянных:
Совместное решение двух уравнений:
Дает следующие значения произвольных постоянных:
После подстановки произвольных постоянных в выражение для
Были произведены контрольные вычисления. При При Это показывает, что полученные данные соответствуют данным из таблицы 1. Расчет остальных токов и напряжений выглядят следующим образом: А) Напряжение
Контроль вычислений:
Б) Напряжение
Контроль вычислений:
В) Ток
Контроль вычислений:
Г) Ток
Контроль вычислений:
Д) Напряжение
Контроль вычислений:
Е) Напряжение
Контроль вычислений:
Результаты вычислений:
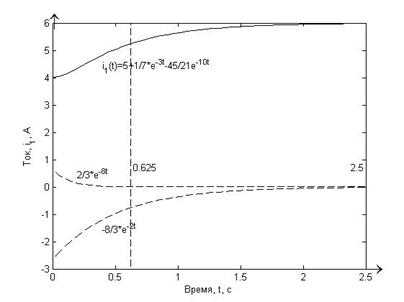
Построенные графики зависимости токов и напряжений от времени по найденным значениям токов и напряжений, представлены в пункте 2.3. Их построение было реализовано с помощью программной среды MatLab. Графики зависимости токов и напряжений от времени Графики зависимости токов и напряжений от времени представлены на рисунках 7.1 - 7.7. Построение точных графиков было реализовано в программной среде MATLAB. Пунктирными вертикальными линиями на графиках отмечен период переходного процесса, который был определен как
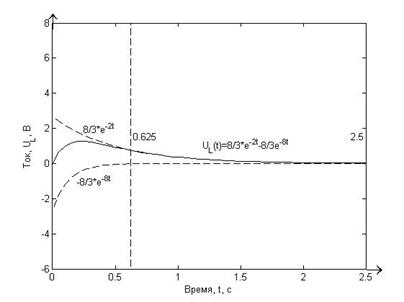
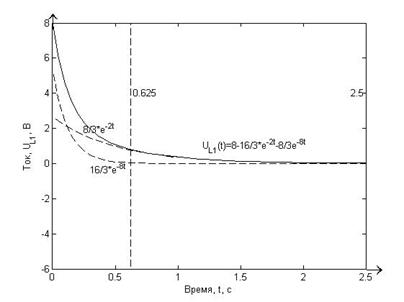
Рисунок 7.1. Точный график функции
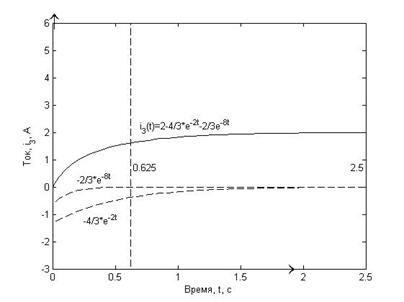
Рисунок 7.2. Точный график функции
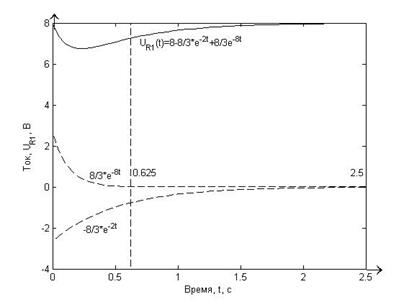
Рисунок 7.3. Точный график функции
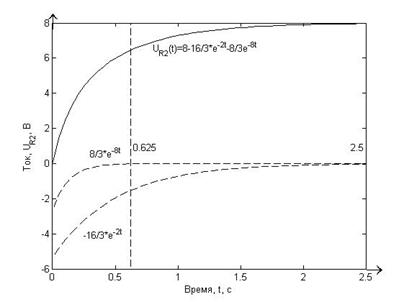
Рисунок 7.4. Точный график функции
Рисунок 7.5. Точный график функции
Рисунок 6.6 Точный график функции
Рисунок 6.7. Точный график функции
По графика можно заметить, что качественные графики, были построены так, чтобы показать как предположительно могут изменяться токи и напряжения. Хоть они и приближены к точным, но все же не учитывают скачки во время переходного процесса. С помощью этих графиков можно определить то, какие из параметров цепи могут изменяться скачкообразно, а следовательно, можно рассчитать параметры цепи, которые следует подкорректировать для корректной работы электрооборудования, исключая его поломку. Расчет экстремумов и точек перегиба на графике Определение экстремумов и точки перегиба Продифференцировано выражение
При Приравнена производная
По таблице значений
Определена вторая производная и, приравняв ее к нулю, найдена точка перегиба напряжения
Выбрано из таблицы ближайшее число Значение напряжения
График для
Рисунок 8 - График Определение обобщенных характеристик цепи Последней практической частью курсовой работы является расчет обобщенных характеристик электрической цепи. Обобщенные характеристики К (р), К (w), h (t), g (t) определяются для схем только с нулевыми начальными условиями. И поэтому в связи с тем что, параметры электрической цепи, которые были взяты для данной курсовой работы имеют ненулевые начальные условия, обобщенные характеристики вычисляться не будут. ЗАКЛЮЧЕНИЕ В данной курсовой работе были выполнены все задачи, а именно: Задача 1 - был проведён анализ литературных источников, касающихся данной курсовой работы. Были найдены все необходимые статьи и материалы по данной теме. Задача 2 – был описан классический метод расчёта переходных процессов в линейных электрических цепях. Были найдены все необходимые формулы для расчёта.
Задача 3 – были определены начальные и конечные условия для всех токов и напряжений в цепи; Задача 4 – были построены качественные графики переходного процесса. Они показывают, какими могут быть графики переходного процесса. Задача 5 – были рассчитаны характеристики переходных процессов классическим методом. Были применены все формулы, найденные в литературных источниках по классическому методу. Задача 6 – были построены точные графики переходного процесса. Задача 7 – были рассчитаны и построены обобщённые характеристики цепи. Цель данной курсовой работы была достигнута, все затронутые задачи решены. Были получены следующие результаты: 1. Рассчитаны значения всех токов и напряжений 2. Построены графики переходного процесса 3. Рассчитаны обобщенные характеристики цепи 4. Найдены значения тока и напряжения в точке максимума и перегиба Как уже было сказано расчет переходных процессов имеет огромное значение в практике, так как зная свойства переходных процессов цепи или устройства при включении можно избежать поломок оборудования. Для создания эквивалентных схем цепи было использовано приложение Microsoft Office Visio 2013. При вычисление переходных процессов и построения качественных графиков в данной курсовой работе была использована программная среда MATLAB, которая сильно облегчила построение качественных графиков в классическом методе расчетов. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 1. Витков М. Г. Основы теории цепей. Лабораторный практикум: Учебное пособие для студентов вузов связи, обучающихся по направлению «Телекоммуникации»/ Н.И. Смирнов. - М.: Радио и связь, 2001.- 224 с. 2. Касаткин А.С. Электротехника: Учеб. Для вузов / А.С. Касаткин, М.В. Немцов. -8-е изд., испр. – М.: Издательский центр «Академия», 2003. – 544 с. 3. Фриск В.В. Основы теории цепей. / Учебное пособие.- М.: ИП РадиоСофт, 2002 -288 с. 4. Бычков Ю.А. Основы теории электрических цепей: Учебник для студентов вузов/ В.М. Золотницкий, Э.П. Чернышев. - СПб.: Лань, 2002.- 464 с. 5. Бакалов Валерий Пантелеевич. Основы теории цепей. Компьютерный тренажерный комплекс: Учебное пособие для студентов вузов по по направлению "Телекоммуникации"/ О.Б. Журавлева, Б.И. Крук. - М.: Радио и связь, 2002.- 200 с.
ПРИЛОЖЕНИЕ А
Таблица 4. Значения функции е-х для разного значения времени
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.47.4 (0.01 с.) |

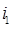 . Тогда уравнение в общем виде имеет вид:
. Тогда уравнение в общем виде имеет вид: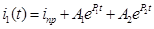
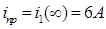 , поэтому:
, поэтому: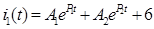
 и
и  была составлена эквивалентная операторная схема цепи (рисунок 6).
была составлена эквивалентная операторная схема цепи (рисунок 6).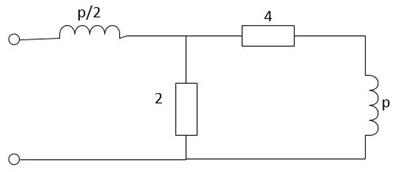
 ). Операторное сопротивление индуктивности
). Операторное сопротивление индуктивности 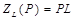 , тогда:
, тогда: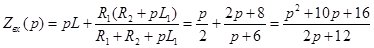
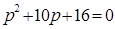
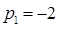 ;
; 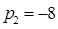
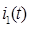 , было получено:
, было получено: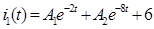
 и
и  . Используя значение самой функции
. Используя значение самой функции 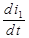 при
при 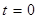 , т.е. были учтены начальные условия. Учитывая, что
, т.е. были учтены начальные условия. Учитывая, что 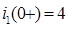 :
: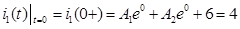
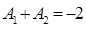
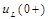 при
при 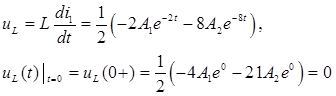
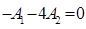
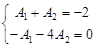
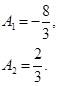
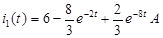
 ,
, 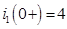
 ,
, 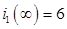
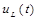 :
: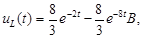
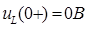
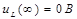
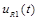 :
: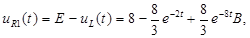
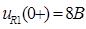
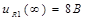
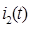 :
: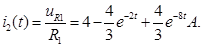
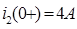
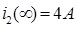
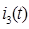 :
: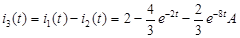
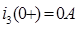
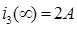
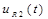 :
: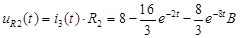 .
.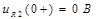
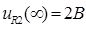
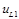 :
: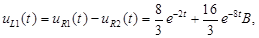
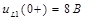
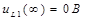
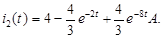
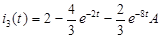
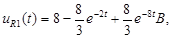
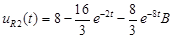
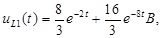
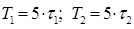 , где
, где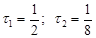
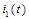
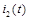
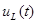
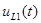
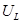 .
.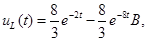
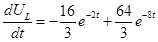
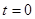 производная
производная 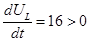 положительна, это означает, что кривая должна идти вверх под некоторым углом.
положительна, это означает, что кривая должна идти вверх под некоторым углом.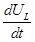 к нулю и найдено максимальное значение функции:
к нулю и найдено максимальное значение функции: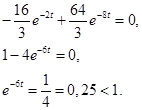
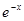 , представленной в приложении 1, выбрано ближайшее число
, представленной в приложении 1, выбрано ближайшее число 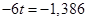 , значит
, значит 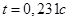
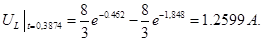
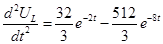 ;
;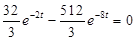 ;
;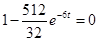 ;
;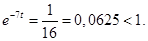
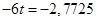 , тогда
, тогда 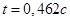 .
.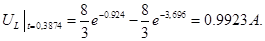
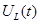 приведен на рисунке 8.
приведен на рисунке 8.