
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование линейной электрической цепиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С ИСТОЧНИКАМИ ПЕРИОДИЧЕСКИХ
Цель работы Изучение и исследование процессов в линейных электрических цепях, содержащих периодические источники ЭДС несинусоидальной формы. Определение коэффициентов, характеризующих форму кривой. Получение с помощью ЭВМ и по справочнику аналитического выражения кривых несинусоидального тока и напряжения. Расчёт электрических цепей с источниками несинусоидальных ЭДС и токов. Основные положения Причиной появления несинусоидальных напряжений и токов в электрических цепях является отличие кривой распределения магнитной индукции в воздушном зазоре от синусоидальной в генераторах переменного тока и наличие нелинейных элементов (катушек с ферромагнитными сердечниками, диодов, тиристоров, люминисцентных ламп и т.д.). Кроме того, для решения ряда технических задач (управление разверткой в осциллографе, телевизоре, синхронизация и цикличность взаимодействия различных элементов автоматики) применяются периодические электрические сигналы несинусоидальной формы. Последние могут содержать гораздо большую и разнообразную информацию, чем гармонические сигналы. Разложение периодической функции f(t) с периодом Т, удовлетворяющей условиям Дирихле, в тригонометрический ряд может быть представлено в двух формах:
(2) Коэффициенты ряда (1) определяются как
Переход от формы ряда (1) к форме ряда (2) осуществляется по формулам
и (4)
а обратный переход – по формулам
(5)
Первое слагаемое в разложении (2) называется постоянной составляющей или нулевой гармоникой, второе – с индексом 1- первой или основной гармоникой, все остальные члены разложения – высшими гармониками. В зависимости от симметрии реальной кривой f(t) тригонометрический ряд может не содержать постоянной составляющей, четных или нечетных гармоник, а также начальных фаз. Если функция f(t) симметрична относительно оси абсцисс рис. 1а),
f(t) f(t) f(t)
t t t
а б г Рис. 1
т.е. удовлетворяет условию f(ωt) = - f(ωt + π), то её разложение не содержит гармоник чётного ряда и постоянной составляющей:
или
Например, тригонометрический ряд Фурье для напряжения прямоугольной формы (рис. 2) имеет вид
0
Рис. 2 Если функция f(t) симметрична относительно оси ординат (рис. 1б), т.е. удовлетворяет условию f(ωt) = f(-ωt), то её разложение не содержит синусов:
Если функция f(t) симметрична относительно начала координат (рис. 1в), то f(ωt) = - f(-ωt), её разложение не содержит постоянной составляющей и косинусов:
Условие симметрии относительно оси абсцисс не зависит от выбора начала отсчёта времени, т.е. является свойством самих кривых, тогда как рассмотренные остальные виды симметрии связаны с выбором начала отсчёта времени. Если генератор ЭДС симметричен, то эдс фазы генератора не содержит гармоник четного ряда. В линейной электрической цепи с постоянными параметрами ток также не будет содержать гармоник четного ряда. Условия прохождения тока в обоих направлениях могут быть неодинаковы (например, цепь с выпрямителем). В этом случае появляется постоянная составляющая и чётные гармоники в кривой тока. Разложение кривых произвольной формы в ряд Фурье можно выполнить графоаналитическим методом. Этот метод основан на замене определённого интеграла суммой конечного числа слагаемых. Тригонометрическая форма ряда Фурье может быть преобразована в комплексную:
(7)
где комплексный коэффициент
Характеристика несинусоидальных величин, представленных рядом Фурье, может быть представлена графически с помощью диаграмм амплитудно-частотного (рис. 3) и фазочастотного (рис. 4) спектров. Эти диаграммы характеризуют форму несинусоидальных кривых, причем первая диаграмма показывает спектральный состав по амплитудам, т.е. представляет зависимость амплитуд гармоник в относительных единицах от частоты, вторая диаграмма выражает зависимость начальных фаз гармоник от частоты.
1
0 w 3w 5w 7w 9w w 0 w 3w 5 w 7w 9w w Рис. 3 Рис. 4 Периодическая несинусоидальная функция f(t) (например, напряжение, ЭДС или ток) характеризуется действующим значением
(8)
Действующие значения не зависят от начальных фаз гармоник и определяются по действующим значениям их гармонических составляющих:
(9) Периодические несинусоидальные кривые имеют следующие характеристики формы. Коэффициент формы кривой f(t) есть отношение действующего значения F к среднему по модулю значению за период Fср:
(10)
Коэффициент амплитуды – отношение максимального значения F к действующему значению функции f(t):
(11)
Коэффициент искажения – отношение действующего значения основной гармоники к действующему значению всей функции:
(12)
Коэффициент гармоник – отношение действующего значения высших гармоник к действующему значению основной гармоники:
(13)
Согласно ГОСТ 13109 – 67, определяющего качество электроэнергии, несинусоидальность формы кривой напряжения, при которой действующее значение всех высших гармоник не превышает 5% действующего значения напряжения основной частоты, длительно допустима на выводах любого приёмника электрической энергии. Активная мощность периодического тока произвольной формы определяется как среднее за период значение мгновенной мощности
Если мгновенные значения напряжения и тока представить в виде ряда Фурье, то после интегрирования
Очевидно, что реактивная мощность
полная мощность
и коэффициент мощности
Для несинусоидального тока, в отличии от синусоидального
Для количественного учёта этого неравенства вводится мощность искажений
Отношение T/S характеризует различие форм кривых тока и напряжения. Расчет токов в линейных разветвленных цепях при действии несинусоидальных периодических напряжений производится для каждой гармоники в отдельности символическим методом; при этом индуктивные и емкостные сопротивления для k-й гармоники равны соответственно kw1L и 1/kw1C. Если kω1L = 1/kω1C, то в цепи имеет место резонанс напряжений. Расчет постоянной составляющей тока производится методами расчета цепей постоянного тока. После этого определяются действующие значения токов и напряжений по формулам (9). Результаты расчёта должны быть представлены в мгновенной форме записи. В тех случаях, когда форма кривой не имеет существенного значения, можно проводить расчёты и строить векторные диаграммы для эквивалентных синусоид тока и напряжения. Эквивалентные синусоиды имеют частоту основной гармоники, их действующие значения равны действующим значениям несинусоидальной функции. Угол сдвига фаз выбирается таким, чтобы активная мощность эквивалентной синусоиды равнялась активной мощности несинусоидального тока. Знак угла берётся по основной гармонике.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.69.25 (0.009 с.) |

 (1)
(1)







 где k = 1, 3, 5, …
где k = 1, 3, 5, … (6)
(6)
 u
u


 t
t





 Fn/Fmax yn
Fn/Fmax yn










 (14)
(14)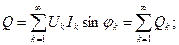 (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19)


