
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разветвлённые электрические цепи, их основные характеристики и уравнения, описывающие состояние цепиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕТРОТЕХНИКИ ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА Учебное пособие для студентов электротехнических специальностей всех форм обучения
Утверждено на заседании ученого совета Протокол № от
Краматорск ДГМА УДК 621. 3.01 ББК 31.21 Ф 33 Авторы: Федоров М.М., д-р техн. наук, професор, Донецкий Национальный технический университет Ткаченко А.А., канд. техн. наук, старший преподаватель, Донбасская государственная машиностроительная академия Кутковой И.П., асcистент, Донбасская государственная машиностроительная академия
Рецензенты: Фамилия И.О., звание, должность, ВУЗ; Фамилия И.О., звание, должность, ВУЗ.
Рекомендовано Міністерством освіти і науки, молоді та спорту України (лист № від)
ISBN ********* В учебном пособии приведены основные топологические свойства цепей, классификация элементов электрической цепи, уравнения, описывающие состояние электрических цепей в виде законов Ома и Кирхгофа. Рассмотрены различные методы расчета и анализа электрических цепей, включая матричные методы, а также основные теоремы электрических цепей и методы преобразования. Впервые сформулированы основные свойства активных трехполюсников и разработаны методы определения параметров их эквивалентных схем замещения. Применение каждого метода проиллюстрировано решенными задачами с детальным объяснением решения. Пособие предназначено для самостоятельного изучения курса «Теоретические основы электротехники» студентами электротехнических и электромеханических специальностей высших учебных заведений.
У навчальному посібнику приведені основні топологічні властивості кіл, класифікация елементів електричного кола, рівняння, що описують стан електричних кіл у вигляді законів Ома і Кирхгофа. Розглянуті різні методи розрахунку і аналізу електричних кіл, включаючи матричні методи, а також основні теореми електрічних кіл і методи перетворення. Вперше сформульовані основні властивості активних триполюсників і розроблені методи визначення параметрів їх еквіва-лентних схем заміщення. Вживання кожного методу проілюстроване вирішеними завданнями з детальним поясненням рішення. Посібник призначений для самостійного вивчення курсу «Теоретичні основи електротехніки» студентами електротехнічних і електромеханічних спеціальностей вищих учбових закладів. УДК 621.3 ББК 31.21
СОДЕРЖАНИЕ ВВЕДЕНИЕ................................................................................................ 5 1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ, ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 7 1.1. Элементы электрической цепи....................................................... 7 1.1.1. Пассивные элементы............................................................ 8 1.1.2. Активные элементы.............................................................. 12 1.2. Разветвленные электрические цепи, их характеристики и уравнения, описывающие состояние цепи....................................................................................... 17 1.2.1. Характеристики разветвленной электрической цепи......... 17 1.2.2. Уравнения для описания процессов электрической цепи. Законы Кирхгофа......................................................................................................... 20 1.2.3. Задачи расчета электрических цепей.................................. 21 2. ЦЕПИ ПОСТОЯННОГО ТОКА............................................................ 22 2.1. Применение законов Кирхгофа для расчета и анализа электрических цепей 22 2.1.1. Использование законов Кирхгофа для схем с источниками напряжений 22 2.1.2. Особенности использования законов Кирхгофа для схем с источниками тока......................................................................................................... 29 2.1.3. Законы Кирхгофа в матричной форме............................... 32 2.2. Метод контурных токов................................................................. 45 2.2.1. Использование метода контурных токов для схем с источниками напряжений................................................................................................... 45 2.2.2. Особенности использования метода контурных токов для схем с источниками тока............................................................................................ 52 2.2.3. Матричные уравнения котурных токов.............................. 55 2.3. Метод узловых потенциалов......................................................... 61 2.3.1. Метод узловых потенциалов для электрических схем общего вида 61 2.3.2. Особенности использования метода узловых потенциалов для схем, содержащих ветви только с источником напряжения........................... 68 2.3.3. Матричные уравнения узловых потенциалов.................... 71 2.4. Теоремы линейных электрических цепей...................................... 78 2.4.1. Баланс мощностей................................................................ 78 2.4.2. Метод наложения................................................................. 79 2.4.3. Метод эквивалентного генератора...................................... 89 2.4.4. Теорема компенсации.......................................................... 97 2.4.5. Свойства взаимности............................................................ 101 2.4.6. Входные и взаимные проводимости ветвей....................... 103
2.4.7. Активный трехполюсник..................................................... 106 2.5. Методы преобразования электрических цепей............................. 125 2.5.1. Расчет разветвленных цепей цепочного типа..................... 126 2.5.2. Взаимное преобразование схем с источниками напряжения и источниками тока................................................................................................. 133 2.5.3. Преобразование электрических цепей, в которых источник тока охватывает несколько ветвей............................................................................. 136 2.5.4. Подключение источников напряжения в ветви, подсоединенные к одному узлу..................................................................................................... 140 2.5.5. Замена параллельных ветвей эквивалентной ветвью......... 146 2.5.6. Взаимное преобразование схем звезда–треугольник........ 147 2.6. Экспериментальные методы исследования свойств цепей постоянного тока 157 2.6.1. Исследование характеристик активных и пассивных элементов цепей постоянного тока.................................................................................... 158 2.6.1.1. Проверка номиналов пассивных резистивных элементов 158 2.6.1.2. Вольтамперные характеристики пассивных элементов цепей постоянного тока................................................................................................ 159 2.6.1.3. Вольтамперные характеристики источников питания.. 160 2.6.2. Экспериментальная проверка закона Ома и законов Кирхгофа 162 2.6.3. Экспериментальная проверка методов расчета................. 164 2.6.4. Экспериментальная проверка метода наложения............. 166 2.6.5. Экспериментальная проверка метода эквивалентного генератора 168 2.6.6. Экспериментальная проверка теоремы компенсации....... 169 2.6.7 Экспериментальная проверка принципа взаимности......... 170 2.6.8. Экспериментальная проверка взаимных преобразований схем звезда–треугольник.................................................................................... 171 СПИСОК ЛИТЕРАТУРЫ.......................................................................... 174
ВВЕДЕНИЕ Курс «Теоретические основы электротехники» является основной дисциплиной, которая служит базой для всех специальных электротехнических дисциплин. Изучение курса теоретических основ электротехники в ВУЗах основывается на знаниях, полученных из курсов физики и математики. Эти знания в курсе теоретических основ электротехники расширяются и развиваются в направлении разработки методов анализа, расчета и экспериментального исследования явлений и процессов, протекающих в электрических и магнитных цепях. Цель данного методического пособия состоит в том, чтобы дать студентам достаточно полное представление об электрических цепях, составных элементах, математических описаниях, основных методах анализа и расчета этих цепей. Данное методическое пособие включает два раздела курса «Теоретические основы электротехники» – «Электрические цепи. Основные понятия и определения» и «Цепи постоянного тока». Материал, изложенный в разделе «Электрические цепи. Основные понятия и определения», базируется на математической подготовке в области дифференциального и интегрального исчислений, линейной и нелинейной алгебры, а также знакомством с основными понятиями и законами электричества и магнетизма, рассматриваемыми в курсе физики. Рассмотрена классификация элементов электрической цепи. Приведены основные топологические свойства цепей, уравнения, описывающие состояние электрических цепей в виде законов Кирхгофа. В разделе «Цепи постоянного тока» рассмотрены вопросы применения законов Кирхгофа для расчета и анализа электрических цепей. Рассмотрены различные методы расчета и анализа электрических цепей, включая матричные методы, а также основные теоремы электрических цепей и методы преобразования. Впервые рассмотрены основные свойства активных трехполюсников. Разработаны методы определения параметров их эквивалентных схем замещения. Предложена методика расчета разветвленных электрических цепей с использованием схем замещения активных трехполюсников. Предлагаемые методы расчета и анализа электрических цепей иллюстрированы конкретными примерами. Знания и навыки, полученные при изучении данного курса, являются базой для освоения таких дисциплин, как: математические основы теории автоматического управления, теория автоматического управления, электропривод, электрические измерения и т. д. Настоящее пособие способствует повышению эффективности и качества самостоятельной работы и совершенствованию практических навыков студентов в решении электрических цепей постоянного тока и используется при подготовке к лекционным и практическим занятиям, а также к выполнению лабораторных работ по курсу «Теоретические основы электротехники».
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ, ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Электрической цепью называют совокупность устройств и объектов, предназначенных для создания, транспортировки, потребления электрической энергии. В электрических цепях следует выделить источники электрической энергии и приемники, которые соединяются между собой каналами связи или соединительными проводами. Источникамиэлектрической энергии называютустройства, в которых, какой-либо вид энергии (механическая, световая, химическая и пр.) преобразуется в электрическую. Источниками электрической энергии являются генераторы, аккумуляторы, солнечные батареи и пр. Например, механическая энергия паровых турбин либо гидротурбин на электростанциях преобразуется в электрическую, в аккумуляторах – химическая энергия преобразуется в электрическую. Приемниками электрической энергии называют устройства, в которых, электрическая энергия преобразуется в другой вид энергии. Приемниками электрической энергии являются двигатели, нагревательные элементы и пр. Электромагнитные процессы в электрической цепи могут быть описаны с помощью понятий электродвижущей силы e(t), тока i(t), напряжения u(t) и др. В общем случае эти параметры электрической цепи являются функцией времени и их величины в произвольным момент времени называются мгновенными значениями. Электрические цепи в которых ток I, напряжение U, электродвижущая сила E не являются функцией времени, называются цепями постоянного тока. Одной из характеристик электрической цепи является потенциал φ.
Элементы электрической цепи
Любое электротехническое устройство может быть описано с помощью электрических схем, которые формируются с помощью идеализированных элементов. Они могут быть пассивными и активными. Пассивные элементы электрической цепи потребляют электрическую энергию, а активные – генерируют ее.
Пассивные элементы
К пассивным элементам относятся резистивный, индуктивный и емкостной элементы. Резистивный элемент
Резистивным называют идеализированный элемент, в котором электрическая энергия преобразуется в тепловую или в другой вид полезной энергии. Обозначение резистивного элемента в электрических схемах приведено на рисунке 1.1.
Рисунок 1.1 – Условное графическое обозначение резистивного элемента
Количественной характеристикой резистивного элемента является сопротивление r (или R), либо величина обратная сопротивлению, называемая проводимостью Функциональная зависимость между током i и напряжением u на зажимах резистивного элемента описывается законом Ома:
Эта зависимость может быть оценена с помощью вольт-амперной характеристики (ВАХ), представленной на рисунке 1.2. В общем случае сопротивление резистивного элемента может быть функцией напряжения или тока. Вольт-амперная характеристика имеет вид прямой линии, когда сопротивление резистивного элемента r не зависит от тока i и напряжения u, и нелинейная, когда r является функциональной зависимостью либо тока i либо напряжения u. Резистивный элемент характеризуется мощностью. Мгновенная мощность:
Средняя мощность, потребляемая резистивным элементом за промежуток времени T равна:
Рисунок 1.2 – Вольт-амперные характеристики резистивных элементов
Для цепей постоянного тока средняя мощность определяется выражением:
Индуктивный элемент Индуктивным называют идеализированный элемент, в котором электрическая энергия преобразуется в энергию магнитного поля, а преобразования в другие виды энергии не происходит. Обозначение индуктивного элемента в электрических схемах приведено на рисунке 1.3.
Рисунок 1.3 – Условное графическое обозначение индуктивного элемента
Функциональная зависимость между напряжением u и током i может быть получена с помощью закона Фарадея, согласно которому:
где
В системе СИ потокосцепление и магнитный поток измеряются в Веберах [Вб]. Тогда, функциональная зависимость между током i и напряжением u на зажимах индуктивного элемента имеет вид:
Свойства индуктивного элемента оценивается с помощью вебер-амперной характеристики (ВбАХ), приведенной на рисунке 1.4.
Рисунок 1.4 – Вебер-амперные характеристики индуктивного элемента
Вебер-амперная характеристика имеет вид прямой линии, когда индуктивность индуктивного элемента L не является функцией тока i и потокосцепления ψ, и нелинейная, когда L является функциональной зависимостью либо i либо ψ. Энергия, запасенная в магнитном поле индуктивности равна:
Для цепей постоянного тока, где
Емкостной элемент Емкостным называют идеализированный элемент, в котором электрическая энергия преобразуется в энергию электрического поля. Преобразования электрической энергии в другие виды энергии не происходит. Обозначение емкостного элемента в электрических схемах приведено на рисунке 1.5.
Рисунок 1.5 – Условное графическое обозначение емкостного элемента
Количественной характеристикой емкостного элемента является емкость Функциональная зависимость между током i и напряжением u на зажимах емкостного элемента иммет вид:
где Свойства емкостного элемента могут быть оценены с помощью кулон-вольтной характеристики, приведенной на рисунке 1.6. Кулон-вольтная характеристика имеет вид прямой линии, когда емкость емкостного элемента С не зависит от напряжения u C и электрического заряда q, и нелинейная, когда С является функциональной зависимостью либо u Cлибо q. Ток емкости характеризует скорость накопления заряда. Если ток больше нуля, то происходит накопление заряда, если меньше нуля – разряд. Для постоянного тока напряжение на зажимах емкости не изменяется во времени, следовательно, ток емкости равен нулю, а сопротивление емкости постоянному току бесконечно велико.
Рисунок 1.6 – Кулон-вольтные характеристики емкостного элемента
Энергия электрического поля, запасенная емкостью равна:
Активные элементы
К активным элементам электрической цепи относятся те элементы, которые содержат в своей структуре источники электрической энергии (генераторы, аккумуляторы, солнечные батареи и т. п.) Характеристикой источников электрической энергии является ЭДС ЭДС источника определяется разностью потенциалов на зажимах источника при отсутствии тока
Рисунок 1.7 – Источник электрической энергии
Рассмотрим основные характеристики источника электрической энергии на примере простейшей цепи постоянного тока, приведенной на рисунке 1.8, включающую в себя источник постоянной ЭДС
Рисунок 1.8 – Простейшая цепь постоянного тока
В электрической цепи протекает ток I и напряжение U на зажимах источника меньше ЭДС источника на величину падения напряжения
В этом случае вольт-амперные характеристики источника, при
Рисунок 1.9 – Внешние характеристики источника питания
Наклон характеристики определяется величиной При При
Рисунок 1.10 – Идеальный источник питания и его ВАХ
Независимо от тока в цепи, напряжение на зажимах такого источника всегда равно ЭДС Е. Исходная электрическая цепь может быть описана с помощью схемы, представленной на рисунке 1.11. Источник представлен эквивалентной схемой в виде последовательного соединения источника напряжения и внутреннего сопротивления
Рисунок 1.11 – Реальная цепь постоянного тока
Мощность, генерируемая источником напряжения равна
Из выражения
Рисунок 1.12 – Исходная схема с источником тока
Где – Величина
Рисунок 1.13 – Идеальный источник тока и его ВАХ
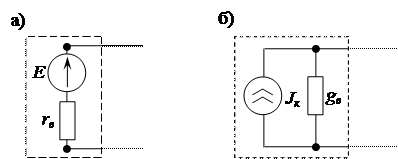
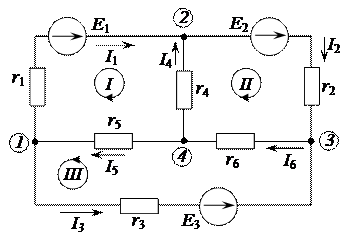
Мощность, генерируемая источником тока равна Таким образом, источник электрической энергии может быть представлен в виде двух эквивалентных схем с источником напряжения (рис. 1.14, а) и с источником тока (рис. 1.14, б). Обе схемы источников электрической энергии являются эквивалентными.
Рисунок 1.14 – Эквивалентные схемы источников энергии – с источником напряжения а) и источником тока б)
Режимы работы электрической цепи определяются на пересечении ВАХ источника и приемника (рис. 1.15).
Рисунок 1.15 – Режим работы исходной цепи
Напряжение на зажимах источника равно напряжению на нагрузке. Для источника напряжения, при изменении сопротивления нагрузки, меняется величина тока, а напряжение на зажимах источника остается постоянным (рис. 1.16).
Рисунок 1.16 – Режимы работы электрической цепи с источником напряжения и приемниками Для источника тока, при изменении сопротивления нагрузки, изменяется напряжение на зажимах источника, а ток остается неизменным (рис. 1.17).
Рисунок 1.17 – Режимы работы электрической цепи с источником тока и приемниками
Для источников электрической энергии также существует понятия переменных источников напряжения и тока. В источниках напряжения независимо от величины и характера сопротивления нагрузки напряжение на зажимах u(t) всегда неизменно, а для источников переменного тока неизменным остается ток iк(t). Внутреннее сопротивление может представлять электрическую цепь, в которой могут находиться пассивные элементы (r, L, C).
ЦЕПИ ПОСТОЯННОГО ТОКА
Особенностью цепей постоянного тока является тот факт, что пассивными элементами являются резистивные элементы, поэтому уравнение состояния электрических цепей (первый и второй законы Кирхгофа), представляет собой систему алгебраических уравнений. В данном разделе рассмотрим различные методы расчета и анализа электрических цепей с линейными резистивными элементами.
Источниками напряжений
Допустим, имеем электрическую цепь постоянного тока, представленную на рисунке. 2.1.
Рисунок 2.1 – Электрическая цепь постоянного тока
Рассмотрим возможности решения основной задачи расчета приведенной разветвленной цепи постоянного тока. Исходными данными для расчета являются параметры активных и пассивных элеметов цепи. Требуется рассчитать токи в ветвях Рассмотрим основные этапы расчета и анализа. 1. Осуществляем предварительный анализ схемы. 1.1. Определяем количество ветвей и узлов схемы, выбираем положительное направление токов в ветвях (рис. 2.1). Количество ветвей - 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.2. Ветвями дерева приняты ветви 4,5,6. Ветви связи (1,2,3) обозначены на схеме пунктирными линиями.
Рисунок 2.2 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. В контур входит одна ветвь связи, добавленная ветвями дерева. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 и 5 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 2, дополненной 4 и 6 ветвями дерева; третий главный контур состоит из ветви связи 3, дополненной 5 и 6 ветвями дерева. Положительное направление обхода контура рекомендуется принимать совпадающим с направлением тока в ветви связи (рис. 2.1 и рис. 2.2.). Число независимых контуров для данной схемы равно 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа. При составлении уравнений учитываем правило знаков. Если ток направлен к узлу, то берем знак ”+”, если от узла, то принимаем знак ”-”. Либо наоборот. По первому закону Кирхгофа:
Таким образом, по первому закону Кирхгофа составлено ( 2.2. По второму закону Кирхгофа. При составлении используют следующее правило знаков. Если направление обхода контура и направление токов в ветви совпадают, то падение напряжения на резистивных элементах ветви берется со знаком ”+”. При несовпадении – знак ”-”. Аналогично учитываются знаки ЭДС источников напряжения. По второму закону Кирхгофа:
Таким образом, по второму закону Кирхгофа составлено В результате имеем систему из 6 уравнений и 6 неизвестных токов, что позволяет осуществить расчет токов в ветвях исходной схемы. Пример 2.1. Рекомендованный порядок расчета рассмотрим на примере электрической схемы, приведенной на рисунке 2.3, параметры которой равны: E 1 = 30 B, Е 2 = 20 В, Е 3 = 20 В, r 1 = 5 Ом, r 2 = 10 Ом, r 3= 8 Ом, r 4 = 8 Ом, r5 = 10 Ом, r 6 = 5 Ом.
Рисунок 2.3 – Электрическая цепь
1. Осуществляем предварительный анализ схемы. 1.1. Количество ветвей – 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.4. Ветвями дерева приняты ветви 4,5,2. Ветви связи (1,3,6) обозначены на схеме пунктирными линиями.
Рисунок 2.4 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 и 2 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 3, дополненной 2 и 5 ветвями дерева; третий главный контур состоит из ветви связи 6, дополненной 5 и 4 ветвями дерева. Положительное направление обхода контура принимаем совпадающим с направлением тока в ветви связи (рис. 2.3 и рис. 2.4). 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа:
2.2. По второму закону Кирхгофа:
3. Подставляем числовые значения в полученную систему уравнений:
Решая данную систему уравнений, определяем токи в ветвях:
4. Проверку решения системы уравнения осуществляем с помощью баланса мощности. 4.1. Мощность, генерируемая источниками:
Суммарная мощность источников:
4.2. Мощность приемников:
Суммарная мощность приемников:
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений Пример 2.2. Рассмотрим пример электрической цепи, с последующей экспериментальной проверкой на стенде УИЛС, приведенной на рисунке 2.5, параметры которой равны: E 1 = 20 B, Е 2 = 15 В, r 1 = 50 Ом, r 2 = 100 Ом, r 3= 300 Ом, r 4 = 200 Ом, r5 = 150 Ом.
Рисунок 2.5 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. 1.1. Количество ветвей – 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.6. Ветвями дерева приняты ветви 2,4. Ветви связи (1,3,5) обозначены на схеме пунктирными линиями.
Рисунок 2.6 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 ветвью дерева. Соответственно, второй главный контур состоит из ветви связи 5, дополненной 2 и 4 ветвями дерева; третий главный контур состоит из ветви связи 3, дополненной 2 ветвью дерева. Положительное направление обхода контура принимаем совпадающим с направлением тока в ветви связи (рис. 2.5 и рис. 2.6). 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа:
2.2. По второму закону Кирхгофа:
3. Подставляем числовые значения в полученную систему уравнений:
Решая данную систему уравнений, определяем токи в ветвях: | ||||||||
|
| Поделиться: |


 . В системе СИ сопротивление измеряется в Омах [Ом], а проводимость - в Сименсах [См].
. В системе СИ сопротивление измеряется в Омах [Ом], а проводимость - в Сименсах [См].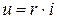 ,
,  .
.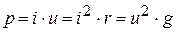 .
. .
.
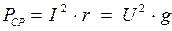 .
.
 ,
, – ЭДС самоиндукции,
– ЭДС самоиндукции, – потокосцепление катушки,
– потокосцепление катушки, - число витков,
- число витков,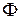 – поток магнитной индукции:
– поток магнитной индукции: .
.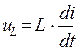 или
или  .
.
 .
. , сопротивление индуктивного элемента представляет собой идеальный проводник, сопротивление которого равно нулю.
, сопротивление индуктивного элемента представляет собой идеальный проводник, сопротивление которого равно нулю.
 . В системе СИ емкость измеряется в Фарадах [Ф].
. В системе СИ емкость измеряется в Фарадах [Ф]. ,
,  ,
, - электрический заряд. В системе СИ электрический заряд измеряется в Кулонах [Кл].
- электрический заряд. В системе СИ электрический заряд измеряется в Кулонах [Кл].
 .
. (рис.1.7) и внутреннее сопротивление
(рис.1.7) и внутреннее сопротивление  .
. . ЭДС направлена от точки с меньшим потенциалом к точке с большим потенциалом.
. ЭДС направлена от точки с меньшим потенциалом к точке с большим потенциалом.
 с внутренним сопротивлением
с внутренним сопротивлением  , соединительных проводов и приемника (например, в виде лампы накаливания).
, соединительных проводов и приемника (например, в виде лампы накаливания).
 на внутреннем сопротивлении источника:
на внутреннем сопротивлении источника: .
. , будут иметь вид прямых линий, изображенных на рисунке 1.9. Ее называют внешней характеристикой.
, будут иметь вид прямых линий, изображенных на рисунке 1.9. Ее называют внешней характеристикой.
 , имеем режим короткого замыкания
, имеем режим короткого замыкания 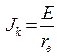 .
. ВАХ источника питания параллельна оси токов (рис. 1.10, б). Такой источник называют идеальным – источником напряжения (рис. 1.10, а).
ВАХ источника питания параллельна оси токов (рис. 1.10, б). Такой источник называют идеальным – источником напряжения (рис. 1.10, а).
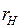 , включающий сопротивление лампы
, включающий сопротивление лампы  и сопротивление соединительных проводов
и сопротивление соединительных проводов  . Источник ЭДС и приемник соединены идеальным проводником, сопротивление которого равно нулю(
. Источник ЭДС и приемник соединены идеальным проводником, сопротивление которого равно нулю( ,
,  ).
).
 . Она расходуется на внутреннее сопротивление источника
. Она расходуется на внутреннее сопротивление источника  и на сопротивления приемника и соединительных проводов
и на сопротивления приемника и соединительных проводов 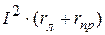 . Т.е.
. Т.е. .
. , следует
, следует  . Откуда
. Откуда  . Этому выражению соответствует электрическая схема, изображенная на рисунке 1.12.
. Этому выражению соответствует электрическая схема, изображенная на рисунке 1.12.
 ,
,  – проводимости внутреннего сопротивления и нагрузки.
– проводимости внутреннего сопротивления и нагрузки. будет уменьшаться при уменьшении
будет уменьшаться при уменьшении  и при
и при  ток
ток  . В данном случае имеем идеальный источник, называемый источником тока (рис. 1.13, а), в цепи с которым независимо от
. В данном случае имеем идеальный источник, называемый источником тока (рис. 1.13, а), в цепи с которым независимо от  ток всегда будет постоянным. Его ВАХ имеет вид, представленный на рисунке 1.13, б.
ток всегда будет постоянным. Его ВАХ имеет вид, представленный на рисунке 1.13, б.
 .
.



 ,
, 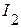 ,
,  ,
,  ,
, 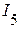 ,
,  . Используя первый и второй законы Кирхгофа можно составить систему из шести уравнений с шестью неизвестными токами, что позволяет решить поставленную задачу.
. Используя первый и второй законы Кирхгофа можно составить систему из шести уравнений с шестью неизвестными токами, что позволяет решить поставленную задачу. , количество узлов -
, количество узлов -  .
.
 .
. (1 узел);
(1 узел); (2 узел);
(2 узел); (3 узел).
(3 узел). ) независимых уравнений.
) независимых уравнений.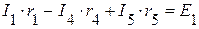 (I контур);
(I контур); (II контур);
(II контур); (III контур).
(III контур). независимых уравнений.
независимых уравнений.
 , количество узлов –
, количество узлов –  . Выбираем положительное направление токов в ветвях (рис. 2.3).
. Выбираем положительное направление токов в ветвях (рис. 2.3).
 (1 узел);
(1 узел); (2 узел);
(2 узел); (3 узел).
(3 узел). (I контур);
(I контур); (II контур);
(II контур); (III контур).
(III контур).
 А,
А,  А,
А,  А,
А, А,
А,  А,
А,  А.
А.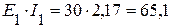 Вт,
Вт, Вт,
Вт, Вт.
Вт. Вт.
Вт. Вт,
Вт,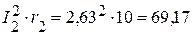 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
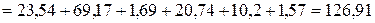 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.
 , количество узлов –
, количество узлов – 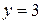 . Выбираем положительное направление токов в ветвях (рис. 2.5).
. Выбираем положительное направление токов в ветвях (рис. 2.5).
 (1 узел);
(1 узел); (2 узел).
(2 узел). (I контур);
(I контур); (II контур);
(II контур);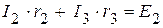 (III контур).
(III контур).



