
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричные уравнения узловых потенциаловСодержание книги
Поиск на нашем сайте
Уравнения узловых потенциалов можно записать в матричной форме:
где
Узловой ток i -го узла равен алгебраической сумме тока источника тока и токов, определяемых ЭДС источников напряжений Уравнение для определения потенциалов узлов имеет вид
где Матрицу узловых проводимостей для соответствующей схемы, можно составить по формуле
где
Рассмотрим схему, приведенную на рисунке 2.31.
Рисунок 2.31 – Электрическая цепь постоянного тока
Граф электрической цепи приведен на рисунке 2.32.
Рисунок 2.32 – Граф цепи постоянного тока
Так как у приведенной схемы четыре узла, то для нахождения токов в ветвях методом узловых потенциалов, необходимо составить три независимых уравнения. Поэтому, матрица соединения узловых проводимостей ветвей состоит из трех строк и шести столбцов:
Диагональная матрица проводимостей Произведение матриц
Матрица узловых проводимостей получается после перемножения матриц
Матрица-столбец потенциалов узлов Матрица-столбец узловых токов
Если матрицу Определитель неопределенной матрицы симметричен относительно главной диагонали. Если вычеркнутая строка не соответствует вычеркнутому столбцу, то и в этом случае получается определенная квадратная матрица, соответствующая независимой системе уравнений. Определитель такой матрицы не имеет симметрии относительно главной диагонали. Если принять равным нулю потенциал того же узла схемы, которой соответствует вычеркнутой строке матрицы
Из этого выражения следует: Пример 2.13. Решить задачу, приведенную в примере 2.4 с помощью матричных уравнений узловых потенциалов. Матрица соединений А состоит из пяти строк и десяти столбцов:
Диагональная матрица проводимостей
Произведение матриц А и
Квадратная матрица узловых проводимостей
Матрица-столбец потенциалов узлов
Матрица-столбец узловых токов
Матрица-столбец ЭДС
Определяем матрицу потенциалов узлов схемы
Узловые потенциалы токи соответственно равны
Матрица-столбец напряжений ветвей U определяем через матрицу потенциалов узлов схемы
Матрица токов ветвей
Токи в ветвях соответственно равны
Токи, рассчитанные в примерах 2.4 и 2.13, совпадают.
Теоремы линейных электрических цепей Баланс мощностей Теорема о балансе мощностей: мощность, генерируемая источниками питания схемы, равняется мощности, потребляемой приёмниками. Если в электрической цепи отсутствуют источники тока, то баланс мощностей имеет вид
где
Если электрические цепи содержат источники тока, то выражение баланса мощностей имеет вид
где Напряжение Правило знаков: если в какой-либо ветви ЭДС Если в цепи имеется несколько источников питания, то возможно, что некоторые их них будут иметь знак ”-”. Это означает, что данный источник питания работает в режиме потребления энергии. Например, заряд аккумуляторной батареи. Однако, суммарная мощность, генерируемая источниками питания, в замкнутой электрической цепи, положительна. Метод наложения
Токи в разветвлённых электрических цепях определяются как алгебраическая сумма токов от каждого источника в отдельности (принцип суперпозиции). Поочерёдно рассчитываются частичные токи от действия каждого источника в отдельности. При этом остальные источники «изымаются» из схемы и вместо них «ставится» их внутреннее сопротивление («закоротка» – источник напряжения, «разрыв» – источник тока). Затем, алгебраическим суммированием токов, полученных от действия каждого источника в отдельности, находим токи в ветвях цепи. Рассмотрим основные этапы расчета на примере электрической цепи, приведенной на рисунке 2.33.
Рисунок 2.33 – Расчетная электрическая схема 1. Осуществляем предварительный анализ. Приведенная схема содержит два источника питания – источник напряжения с ЭДС 2. Рассчитываем частичные токи от действия источника напряжения 2.1. Из исходной схемы удаляем источник тока (заменяем его внутренним сопротивлением
Рисунок 2.34 – Схема для расчета частичных токов от действия Е1
2.2. Определяем входное сопротивление цепи и сопротивления на участках цепи.
2.3. Определяем частичные токи. 2.3.1. Частичный ток 2.3.2. Для определения частичных токов
2.3.3. Частичные токи
3. Определяем частичные токи от действия источника тока 3.1. Из исходной схемы удаляем источник напряжения (заменяем его внутренним сопротивлением
Рисунок 2.35 – Схема для расчета частичных токов от действия Jk5
3.2 Определяем входное сопротивление цеп и сопротивления на участках цепи:
3.3. Рассчитываем частичные токи в ветвях от действия источника тока 3.3.1. Напряжение на зажимах источника тока:
3.3.2. Частичные токи: 3.3.3. Напряжение на зажимах 13: 3.3.4. Частичные токи 4. Определяем токи в исходной схеме, как алгебраическую сумму частичных токов:
Пример 2.14. Рассмотрим порядок расчета на конкретном примере элетрической цепи, приведенной на рисунке 2.36, с параметрами E1 = 50 (B), Е5 = 60 В, Jk4 = 5 А, r1 = 10 Ом, r2 = 8 Ом, r3= 15 Ом, r4 = 20 Ом.
Рисунок 2.36 - Схема электрической цепи
1. Осуществляем предварительный анализ. Приведенная схема содержит три источника питания – источник напряжения с ЭДС 2. Рассчитываем частичные токи ( 2.1. Удаляем из исходной схемы источник напряжения
Рисунок 2.37 - Схема для расчета частичных токов от действия источника напряжения Е1 2.2. Рассчитываем частичные токи. 2.2.1. Частичные токи 2.2.2. Частичные токи
3. Рассчитываем частичные токи ( 3.1. Удаляем из исходной схемы источник напряжения
Рисунок 2.38 - Схема для расчета частичных токов от действия источника напряжения Е5 3.2. Рассчитываем частичные токи. 3.2.1. Частичный ток 3.2.2. Частичные токи
4. Рассчитываем частичные токи ( 4.1. Удаляем из исходной схемы источники напряжения
Рисунок 2.39 - Схема для расчета частичных токов от действия источника тока Jk4
4.2. Рассчитываем входное сопротивление цепи относительно зажимов 13:
4.3. Определяем частичные токи от действия источника тока 4.3.1. Для определения частичных токов
4.3.2. Частичные токи:
5. Рассчитываем токи в исходной схеме:
6. Проверяем решение, составив баланс мощностей. 6.1. Мощность источников:
где
Знак ”-” указывает на то, что первый источник работает в режиме потребителя электроэнергии (например, зарядка аккумулятора). Суммарная мощность источников:
6.2. Мощность приемников:
Суммарная мощность приемников:
6.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении Пример 2.15. Рассмотрим решение задачи, приведенной в примере 2.2, методом наложения. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.40. 1. Осуществляем предварительный анализ схемы. Приведенная схема содержит два источника питания – источник напряжения с ЭДС
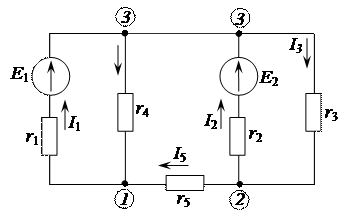
Рисунок 2.40 – Электрическая цепь постоянного тока
2. Рассчитываем частичные токи ( 2.1. Удаляем из исходной схемы источник напряжения
Рисунок 2.41 - Схема для расчета частичных токов от действия источника напряжения Е1
2.2. Рассчитываем входное сопротивление цепи относительно зажимов 34:
2.3. Рассчитываем частичные токи. 2.3.1. Частичный ток 2.3.2. Для определения частичных токов
2.3.3. Частичные токи
2.3.4. Для определения частичных токов
2.3.5. Частичные токи
3. Рассчитываем частичные токи ( 3.1. Удаляем из исходной схемы источник напряжения
Рисунок 2.42 - Схема для расчета частичных токов от действия источника напряжения Е2
3.2. Рассчитываем входное сопротивление цепи относительно зажимов 35:
3.3. Рассчитываем частичные токи. 3.3.1. Частичный ток 3.3.2. Для определения частичных токов
3.3.3. Частичные токи
3.3.4. Для определения частичных токов
3.3.5. Частичные токи
4. Рассчитываем токи в исходной схеме:
Токи в ветвях, рассчитанные в примерах 2.2 и 2.15, совпадают.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

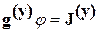 ,
, - квадратная матрица узловых проводимостей;
- квадратная матрица узловых проводимостей; - матрица-столбец потенциалов узлов;
- матрица-столбец потенциалов узлов; - матрица-столбец узловых токов.
- матрица-столбец узловых токов. .
. ,
, - матрица, обратная матрице
- матрица, обратная матрице  .
. ,
, - матрица соединений;
- матрица соединений; - диагональная матрица проводимостей ветвей;
- диагональная матрица проводимостей ветвей; - транспортированная матрица соединений.
- транспортированная матрица соединений.
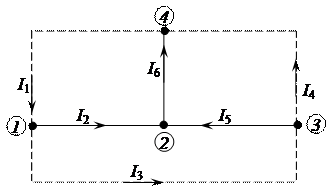
 .
. .
. .
. и
и 


 .
. .
. .
.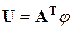 , где положительное направление напряжения
, где положительное направление напряжения  совпадает с положительным направлением тока в ветви. Это получается из формул для напряжения каждой ветви. Например, для схемы (рис. 2.31)
совпадает с положительным направлением тока в ветви. Это получается из формул для напряжения каждой ветви. Например, для схемы (рис. 2.31)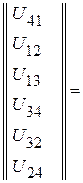

 .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
. .
.


 .
. .
.
 .
.
 .
.

 .
. В,
В,  В,
В,  В,
В, В,
В,  В.
В.

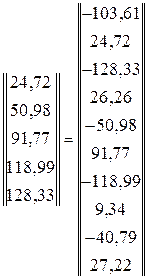



 =
=  .
. А,
А, 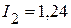 А,
А,  А,
А,  А,
А,  А,
А, А,
А,  А,
А, 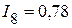 А,
А,  А,
А,  А.
А. ,
, – суммарная мощность, генерируемая источниками напряжения,
– суммарная мощность, генерируемая источниками напряжения, – суммарная мощность, потребляемая приемниками.
– суммарная мощность, потребляемая приемниками. ,
, – суммарная мощность генерируемая источниками тока.
– суммарная мощность генерируемая источниками тока. определяется с помощью второго закона Кирхгофа.
определяется с помощью второго закона Кирхгофа. и ток
и ток 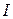 совпадают по направлению, то берется знак ”+”. Аналогично, при положительном направлении
совпадают по направлению, то берется знак ”+”. Аналогично, при положительном направлении  и
и  берется знак ”+” (положительное направление
берется знак ”+” (положительное направление 
 и источник тока
и источник тока 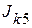 , ветвей
, ветвей  , ветвей с источником тока
, ветвей с источником тока  , следовательно, неизвестных токов ветвях
, следовательно, неизвестных токов ветвях  .
. ). Полученная схема имеет вид, приведенный на рисунке 2.34.
). Полученная схема имеет вид, приведенный на рисунке 2.34.
 .
. :
:  .
. ,
,  ,
,  необходимо определить напряжение
необходимо определить напряжение  на зажимах 13. Оно соответственно равно:
на зажимах 13. Оно соответственно равно: или
или  .
. ,
,  .
. ). Полученная схема имеет вид, приведенный на рисунке 2.35.
). Полученная схема имеет вид, приведенный на рисунке 2.35.


 .
. .
.
 .
. .
.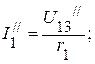
 .
.



 .
.
 , и источник тока
, и источник тока  , ветвей
, ветвей  ,
,  ,
,  ,
,  ) от действия источника напряжения
) от действия источника напряжения 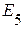 и источник тока
и источник тока  и заменяем их внутренними сопротивлениями. В результате получаем схему, приведенную на рисунке 2.37.
и заменяем их внутренними сопротивлениями. В результате получаем схему, приведенную на рисунке 2.37.
 А,
А,  А.
А. А.
А. ,
,  ,
,  ,
,  ,
,  ) от действия источника напряжения
) от действия источника напряжения 
 А.
А. А,
А, А,
А, А.
А. ,
,  ,
,  ,
,  ,
,  ) от действия источника тока
) от действия источника тока 
 Ом.
Ом. . Оно соответственно равно:
. Оно соответственно равно: B.
B. А,
А, А,
А, А,
А,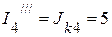 А.
А. А;
А; А;
А; А;
А; А;
А; А.
А. Вт,
Вт, Вт,
Вт, Вт,
Вт, – напряжение на зажимах источника тока, равное
– напряжение на зажимах источника тока, равное B.
B.
 Вт.
Вт. Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.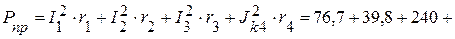
 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%. , ветвей
, ветвей  , узлов
, узлов 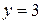 .
.

 Ом.
Ом. мА.
мА. , необходимо определить напряжение
, необходимо определить напряжение  B.
B. мА,
мА, мА.
мА. . Оно соответственно равно:
. Оно соответственно равно: B.
B. мА,
мА, мА.
мА. ,
,  ,
,  ,
,  ,
,  ) от действия источника напряжения
) от действия источника напряжения  и заменяем его внутренним сопротивлением. В результате получаем схему, приведенную на рисунке 2.42.
и заменяем его внутренним сопротивлением. В результате получаем схему, приведенную на рисунке 2.42.
 Ом.
Ом.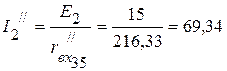 мА.
мА.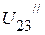 . Оно соответственно равно:
. Оно соответственно равно: B.
B. мА,
мА, мА.
мА. . Оно соответственно равно:
. Оно соответственно равно: B.
B. мА,
мА, мА.
мА. мА;
мА; мА;
мА;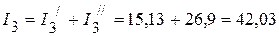 мА;
мА; мА;
мА; мА.
мА.


