
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подсоединенных к одному узлуСодержание книги
Поиск на нашем сайте
Во все ветви электрической цепи, подсоединенные к одному узлу (рис. 2.101), можно включить одинаковые источники напряжения, ЭДС которых равна по величине и направлена к узлу, либо от узла. Подобное включение является эквивалентным, так как в исходной схеме токораспределение остается прежним.
Рисунок 2.101 – Узел электрической цепи
Справедливость такого включения следует из второго закона Кирхгофа, согласно которому, при обходе контура, узел встречается только один раз. Подобное преобразование рационально проводить для электрических схем, у которых имеются ветви только с одним источником напряжения. Рассмотрим указанное преобразование на примере электрической цепи, изображенной на рисунке 2.102 а. В первую, вторую и четвертую ветви (рис. 2.102 б) включены источники напряжения по величине равные ЭДС
Рисунок 2.102 – Преобразование электрической цепи
Так как в четвертой ветви включены источники напряжения равные по величине и противоположные по направлению, то потенциалы узлов
Рисунок 2.103 – Преобразованная электрическая цепь Таким образом, подобное преобразование позволяет уменьшить количество узлов в расчетной схеме.
Пример 2.26. Рассмотрим преобразование электрических цепей, в которых источники напряжения к одному узлу, на примере электрической цепи, приведенной рисунке 2.104, параметры которой Е1 = 20 В, Е2 = 15 В, r3 = 50 Ом, r4 = 150 Ом, r5 = 200 Ом, r6 = 100 Ом.
Рисунок 2.104 –Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – Первая и вторая ветви содержат только источники напряжения с ЭДС При нахождении токов в ветвях, например, методом непосредственного применения законов Кирхгофа, необходимо составить систему уравнений из шести неизвестных токов. При нахождении токов в ветвях, например, методом контурных токов, необходимо составить систему уравнений из трех неизвестных контурных токов. Нахождение токов в ветвях, методом узловых потенциалов, невозможно, т.к. проводимости первой и второй ветви равны 2. Используя, свойство подключения источников напряжения в ветви, подсоединенные к одному узлу, преобразуем электрическую цепь, приведенную на рисунке 2.104.
В первую, пятую и шестую ветви (рис. 2.105) включены источники напряжения по величине равные ЭДС
Рисунок 2.105 – Преобразование электрической цепи постоянного тока
Так как в первой и второй ветвях включены источники напряжения равные по величине и противоположные по направлению, то потенциалы узлов
Рисунок 2.106 – Преобразованная электрическая цепь Таким образом, количество узлов в расчетной схеме уменьшилось до двух. 3. Рассчитываем токи в преобразованной электрической цепи постоянного тока. 3.1. Осуществляем предварительный анализ схемы. Количество ветвей – 3.2. Рассчитываем токи в ветвях методом узловых потенциалов. Потенциал первого узла принимаем равным нулю: 3.2.1. Составляем уравнение для определения потенциала
3.2.1.1. Подставляем числовые значения и находим потенциал 3.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
Узловые токи
3.2.1.3. После подстановки цифровых значений, определяем потенциал 3.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.106.
3.4. Используя первый закон Кирхгофа, определяем токи
4. Проверяем решение, составив баланс мощностей. 4.1. Мощность, генерируемая источниками питания:
Суммарная мощность источников:
4.2. Мощность, потребляемая приемниками:
Суммарная мощность, потребляемая приемниками:
4.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении 2.5.5. Замена параллельных ветвей эквивалентной ветвью
Допустим, имеется схема, представленная на рисунке 2.107.
Рисунок 2.107 – Схема электрической цепи
Доказательство: На первом этапе ветви с источниками напряжения и последовательно соединенными резистивными сопротивлениями, заменим эквивалентными ветвями с источниками тока (рис. 2.108).
Рисунок 2.108 – Доказательство замены параллельных ветвей
В результате получим схему с параллельно соединенными источниками тока и ветви с параллельно соединенными сопротивлениями. Ветви с параллельно соединенными источниками тока заменяем эквивалентной схемой:
Ветви с параллельно соединенными сопротивлениями заменяем эквивалентной схемой:
Подобное доказательство можно обосновать с помощью метода узловых потенциалов. Принимаем потенциал точки
2.5.6. Взаимное преобразование схем звезда-треугольник Соединение, представленное на рисунке 2.109 а, называют трехлучевой звездой, а на рис. 2.109 б – треугольник сопротивлений. Ставится задача осуществить преобразование звезды сопротивлений в эквивалентный треугольник и наоборот. В общем случае звезда (треугольник) сопротивлений подключены к разветвленной схеме в узлах 1, 2, 3. Преобразования должны быть эквивалентными, т.е. в результате преобразований в остальной части схемы никаких изменений нет. Токи
Рисунок 2.109 – Трехлучевая звезда и треугольник сопротивлений
Для доказательства рассмотрим преобразования треугольника сопротивлений (рис. 2.109 б) в эквивалентную звезду схему треугольник (рис. 2.109 а). В этом случае исходными данными являются величины сопротивлений треугольника Из схемы треугольник (рис. 2.109 б), согласно второго закона Кирхгофа, имеем:
Используя первый закон Кирхгофа для 1 и 2 узлов, соответственно получим:
Подставим полученные выражения, в уравнение, составленное по второму закона Кирхгофа. В результате имеем:
Тогда напряжение
Рассмотрим схему звезда (рис. 2.109 а). Для данной схемы
Сравнивая полученные выражения для U 12,
Так как схемы эквивалентные то напряжение одинаково и коэффициенты при токах
Пример 2.27. Рассмотрим эффективность преобразование треугольника сопротивлений в звезду сопротивлений. 1. Исходная схема (рис. 2.110 а) содержит 2. Преобразовываем треугольник сопротивлений
В результате преобразования получим эквивалентную схему, представленную на рисунке 2.110 б.
Рисунок 2.110 – Преобразование треугольника сопротивлений в эквивалентную звезду
Таким образом, после преобразования произошло упрощение схемы: вместо шести ветвей в первой схеме получили три ветви во второй; вместо четырех узлов в первой схеме получили два узла во второй.
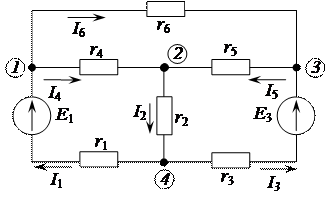
Пример 2.28. Рассмотрим пример взаимных преобразований треугольник–звезда на конкретном примере. В схеме, приведенной на рисунке 2.111, заданы напряжения источников ЭДС Е1 = 20 В, Е3 = 15 В и значения сопротивлений r 1 = 150 Ом, r 2 = 50 Ом, r 3 = 75 Ом, r 4 = 1000 Ом, r 5 = 800 Ом, r 6 = 200 Ом. Определить токи ветвей.
Рисунок 2.111 – Исходная электрическая цепь постоянного тока
1. Исходная схема (рис. 2.111) содержит
2. Преобразовываем треугольник сопротивлений
В результате преобразования получим эквивалентную схему, представленную на рисунке 2.112.
Рисунок 2.112 – Преобразование треугольника сопротивлений в эквивалентную звезду
Таким образом, после преобразования произошло упрощение схемы: вместо шести ветвей в исходной схеме получили три ветви в преобразованной схеме; вместо четырех узлов в исходной схеме получили два узла в преобразованной схеме. 3. Рассчитываем токи в электрической схеме, приведенной на рисунке 2.112, методом узловых потенциалов. 3.1. Осуществляем предварительный анализ схемы. Количество ветвей – 3.2. Рассчитываем токи в ветвях методом узловых потенциалов. Потенциал четвертого узла принимаем равным нулю: 3.2.1. Составляем уравнение для определения потенциала
5.2.1.1. Подставляем числовые значения и находим потенциал 5.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
Узловые токи
5.2.1.3. После подстановки цифровых значений, определяем потенциал 5.2.2. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.112.
3.2.5. Используя второй закон Кирхгофа, определяем токи
3.2.6. Используя первый закон Кирхгофа, определяем ток
4. Проверяем решение, составив баланс мощностей. 4.1. Мощность, генерируемая источниками питания:
Суммарная мощность источников:
4.2. Мощность, потребляемая приемниками:
Суммарная мощность, потребляемая приемниками:
4.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении
Возможно и обратное преобразование – звезды сопротивлений в эквивалентный треугольник (рис. 2.113).
Рисунок 2.113 – Треугольник сопротивлений и трехлучевая звезда
В этом случае исходными данными являются сопротивления Рассмотрим схему звезда (рис. 2.113 б). Ток
Из метода узловых потенциалов Тогда ток
Из схемы треугольник (рис. 2.113 а), имеем: Ток Тогда ток
Сравнивая ток
Аналогично Если в вышеуказанные формулы вместо проводимостей
В общем виде формулы преобразования имеют вид:
Пример 2.29. Рассмотрим пример взаимных преобразований звезда–треугольник на конкретном примере. В схеме, приведенной на рисунке 2.114 а, заданы ЭДС Е = 20 В и значения сопротивлений r 1 = 4 Ом, r 2 = 1 Ом, r 3 = 1 Ом, r 4 = 2 Ом, r 5 = 4 Ом, r 6 = 5 Ом. Определить токи ветвей.
Рисунок 2.114 – Электрическая схема 1. Расчет токов целесообразно осуществлять, преобразуя предварительно звезду
2. Токи в ветви
3. Ветви
4. Ветви
5. Общий ток: 6. Определяем напряжение
7. Токи
8. Ток
9. Ток
10. Ток
11. Ток
12. Проверяем решение системы уравнений, составив баланс мощностей. 12.1. Мощность, генерируемая источником напряжения:
12.2.Мощность приемников:
Суммарная мощность приемников:
12.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.162.189 (0.009 с.) |


 и направлены от узла.
и направлены от узла.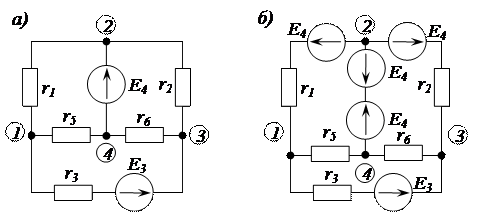
 и
и  равны. В результате схема имеет вид, представленный на рисунке 2.103.
равны. В результате схема имеет вид, представленный на рисунке 2.103.

 , количество узлов –
, количество узлов –  .
. и
и  соответственно.
соответственно. (отсутствуют сопротивления r1 и r2).
(отсутствуют сопротивления r1 и r2).
 и
и  и
и 
 , количество узлов –
, количество узлов –  .
. . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал  .
. См;
См;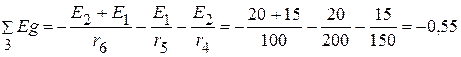 А.
А. :
:  В.
В. мА,
мА, мА,
мА, мА,
мА, мА.
мА. и
и  , в электрической цепи, приведенной на рисунке 2.105:
, в электрической цепи, приведенной на рисунке 2.105: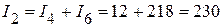 мА;
мА; мА.
мА. Вт,
Вт, Вт.
Вт. Вт.
Вт. Вт,
Вт, Вт,
Вт, Вт,
Вт,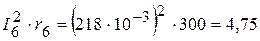 Вт.
Вт.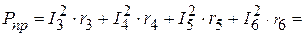
 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.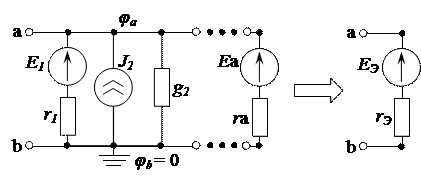

 .
. .
. . Тогда
. Тогда ,
,  .
.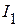 ,
,  и потенциалы
и потенциалы 
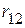 ,
,  ,
, 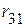 . Необходимо определить величины сопротивлений эквивалентной звезды –
. Необходимо определить величины сопротивлений эквивалентной звезды –  ,
,  ,
,  .
.
 ,
,  .
. , откуда
, откуда .
. между узлами 1 и 2:
между узлами 1 и 2:
 .
. .
.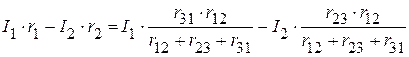 .
.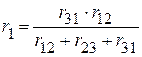 ,
,  ,
,  .
. ветвей и
ветвей и  ,
, 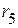 ,
, 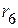 в эквивалентную звезду
в эквивалентную звезду 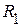 ,
,  ,
,  , сопротивления которой соответственно равны:
, сопротивления которой соответственно равны: ,
,  ,
,  .
.
 узла.
узла. ,
,  ,
, 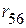 , сопротивления которой соответственно равны:
, сопротивления которой соответственно равны: Ом,
Ом, Ом,
Ом, Ом.
Ом.
 , количество узлов –
, количество узлов –  . Следовательно, необходимо определить потенциал пятого узла
. Следовательно, необходимо определить потенциал пятого узла  .
.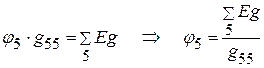 .
.
 См;
См; мА.
мА. В.
В. мА,
мА, мА,
мА, мА.
мА. и
и  в электрической цепи, приведенной на рисунке 2.111:
в электрической цепи, приведенной на рисунке 2.111: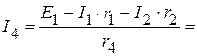
 мА;
мА;
 мА.
мА. в электрической цепи, приведенной на рисунке 2.111:
в электрической цепи, приведенной на рисунке 2.111: мА.
мА. Вт,
Вт, Вт.
Вт.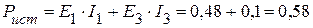 Вт.
Вт. Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.

 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.
 ,
, 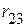 ,
, 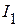 равен:
равен: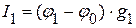 .
. .
.
 .
. .
.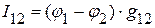 ,
,  .
. .
.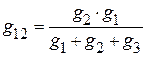 ,
,  .
. .
. ,
,  ,
,  ,
,  подставить величины сопротивлений
подставить величины сопротивлений 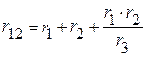 .
.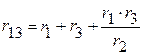 ;
;  .
.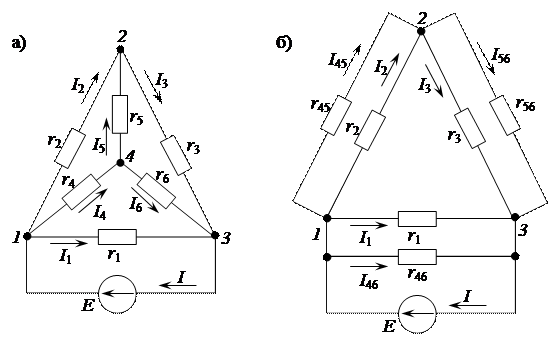
 в треугольник по схеме, приведенной на рисунке 2.114 б. В соответствии с формулами преобразования звезды сопротивлений в треугольник
в треугольник по схеме, приведенной на рисунке 2.114 б. В соответствии с формулами преобразования звезды сопротивлений в треугольник Ом,
Ом, Ом,
Ом, Ом.
Ом. А.
А. Ом,
Ом, Ом.
Ом. и
и  соединены последовательно:
соединены последовательно: Ом.
Ом. А.
А. и
и 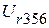 :
: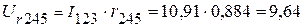 В,
В, В.
В. А,
А,  А.
А. в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 2:
в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 2: А.
А. А.
А. А.
А.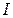 в ветви с источником ЭДС в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 1:
в ветви с источником ЭДС в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 1: А.
А. Вт.
Вт. Вт,
Вт,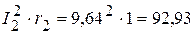 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт,
 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.


