
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет разветвленных цепей цепочного типаСодержание книги
Поиск на нашем сайте
В основе метода расчета подобных цепей используются методы преобразования последовательно и параллельно соединенных элементов, а также закон Ома.
Пример 2.22. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.83, с параметрами: E =200 B, r1 = 8 Ом, r2/ = 5 Ом, r2// = 15 Ом, r3 =8 Ом, r4 = 10 Ом, r5 = 20 Ом, r6 = 30 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
Рисунок 2.83 – Расчетная схема электрической цепи 1. Определяем входное сопротивление всей цепи. 1.1. На первом этапе последовательно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.84.
Рисунок 2.84 – Преобразованная электрическая цепь
1.2. Последовательно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.85.
Рисунок 2.85 – Преобразованная электрическая цепь
1.3. Параллельно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.86.
Рисунок 2.86 – Преобразованная электрическая цепь
1.4. Определяем входное сопротивление всей цепи:
2. Определяем токи в ветвях. С этой целью используем закон Ома. 2.1. Ток 2.2. Определяем токи 2.2.1. Из схемы, приведенной на рисунке 2.86, следует
2.2.2. Тогда токи в ветвях:
2.3. Определяем токи 2.3.1. Из схемы, приведенной на рисунке 2.84, следует
2.3.2. Тогда токи в ветвях:
3. Проверяем решение, составив баланс мощностей. 3.1. Мощность, генерируемая источником питания:
3.2. Мощность, потребляемая приемниками:
Суммарная мощность, потребляемая приемниками:
3.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении Пример 2.23. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.87, с параметрами: E =21 B, r1 =100 Ом, r2 =200 Ом, r3 =50 Ом, r4 =150 Ом, r5 =75 Ом, r6 =300 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
Рисунок 2.87 – Расчетная схема электрической цепи 1. Определяем входное сопротивление всей цепи. 1.1. На первом этапе параллельно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.88.
Рисунок 2.88 – Преобразованная электрическая цепь
2.2. Последовательно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.89.
Рисунок 2.89 – Преобразованная электрическая цепь
2.3. Параллельно соединенные сопротивления
В результате схема имеет вид, представленный на рисунке 2.90.
Рисунок 2.90 – Преобразованная электрическая цепь
2.4. Определяем входное сопротивление всей цепи:
3. Определяем токи в ветвях. С этой целью используем закон Ома. 2.1. Ток 2.2. Определяем токи 2.2.1. Из схемы, приведенной на рисунке 2.90, следует
2.2.2. Тогда токи в ветвях:
2.3. Определяем токи 2.3.1. Из схемы, приведенной на рисунке 2.88, следует
2.3.2. Тогда токи в ветвях:
3. Проверяем решение, составив баланс мощностей. 3.1. Мощность, генерируемая источником питания:
3.2. Мощность, потребляемая приемниками:
Суммарная мощность, потребляемая приемниками:
3.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении 2.5.2. Взаимное преобразование схем с источником напряжения и с источником тока Ранее были рассмотрены схемы с взаимным преобразованием схем с источником тока и источником напряжения (рис. 2.91)
Рисунок 2.91 – Эквивалентные схемы источников энергии – с источником напряжения а) и источником тока б)
Обе схемы источников электрической энергии являются эквивалентными.
Пример 2.24. Рассмотрим замену источника напряжения источником тока на примере простейшей электрической цепи представленной на рисунке 2.92 с параметрами E =20 B, rв =10 Ом, rн = 90 Ом. Требуется определить токи во всех ветвях электрической цепи с источником и напряжения и замененной электрической цепи с источником тока, проверить найденные значения токов, составив баланс мощностей.
Рисунок 2.92 – Электрическая цепь с источником напряжения
Последовательное соединение источника напряжение с ЭДС
Внутренняя проводимость источника тока равна:
После преобразования схема будет иметь вид, представленный на рисунке 2.93.
Рисунок 2.93 – Электрическая цепь с источником тока
1. Определяем параметры и составляем баланс мощностей схемы, приведенной на рисунке 2.92. 1.1. Ток в цепи равен
1.2. Напряжение на нагрузке rн, равное напряжению на выводах источника напряжения
1.3. Мощность, генерируемая источником питания:
1.4. Мощность, потребляемая приемником:
1.5. Из сравнения генерируемой мощности источником и потребляемой мощности приемником, следует, что погрешность вычислении
2. Определяем параметры и составляем баланс мощностей схемы, приведенной на рисунке 2.93. 1.1. Ток в цепи равен
1.2. Напряжение на нагрузке rн, равное напряжению на выводах источника тока
1.3. Ток на снутренней проводимости источника тока
1.4. Мощность, генерируемая источником тока:
1.5. Мощность, потребляемая приемником:
1.6. Из сравнения генерируемой мощности источником и потребляемой мощности приемником, следует, что погрешность вычислении
2.5.3. Преобразование электрических цепей, в которых источник тока охватывает несколько ветвей
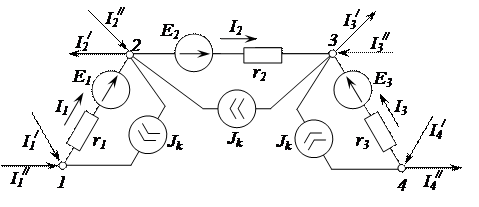
Допустим, имеется часть электрической схемы, представленная на рисунке 2.94, в которой выделены узлы 1, 2, 3 и 4.
Рисунок 2.94 – Электрическая цепь Между узлами 1 и 4 включен источник тока. Необходимо избавиться от ветви с источником тока с целью уменьшения количества ветвей. Преобразования должны быть эквивалентными, т.е. с сохранением основных энергетических соотношений (например, баланс мощности, законы Кирхгофа). На первом этапе источник тока разобьем на три источника тока, подсоединенных между 1 и 2, 2 и 3, 3 и 4 узлами (рис. 2.95).
Рисунок 2.95 – Эквивалентная электрическая цепь после переноса источника тока
Эти измененния касаются 2 и 3 узла. Они эквивалентны, т.к. к каждому узлу мы подсоединили по две ветви с источниками тока На следующем этапе параллельно подсоединенные источники тока, заменяем источниками напряжения: В результате электрическая схема, приведенная на рисунке 2.74, уменьшится на одну ветвь (рис. 2.96).
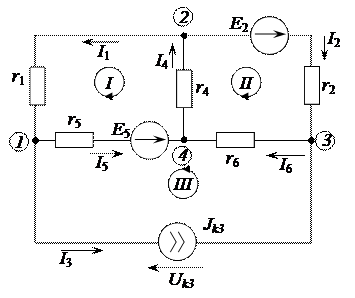
Рисунок 2.96 – Эквивалентная электрическая цепь Пример 2.25. Рассмотрим преобразование электрических цепей, в которых источник тока охватывает несколько ветвей, на примере электрической цепи, рассматриваемой в примере 2.3 и приведенной рисунке 2.97, параметры которой Jk3 = 3 А, Е2 = 50 В, Е5 = 60 В, r1 = 6 Ом, r2 = 10 Ом, r4 = 8 Ом, r5 = 10 Ом, r6 = 5 Ом.
Рисунок 2.97 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – 2. Применяем преобразование электрических цепей, в которых источник тока охватывает несколько ветвей. В результате схема приобретает вид, представленный на рисунке 2.98.
Рисунок 2.98 – Эквивалентная электрическая цепь постоянного тока
3. Параллельно подсоединенные источники тока, заменяем источниками напряжения
В результате схема приобретает вид, представленный на рисунке 2.99.
Рисунок 2.99 – Эквивалентная электрическая цепь постоянного тока
В результате электрическая схема, приведенная на рисунке 2.99, уменьшилась на три ветви и два узла. 4. Применяя свойства последовательного соединение резистивных элементов и последовательного соединение ЭДС, для электрической цепи, изображенной на рисунке 2.99, получим эквивалентную электрическую цепь постоянного тока, представленную на рисунке 2.100.
Рисунок 2.100 – Эквивалентная электрическая цепь постоянного тока
На приведенной схеме,
5. Рассчитываем токи в эквивалентной электрической цепи постоянного тока. 5.1. Осуществляем предварительный анализ схемы. Количество ветвей – 5.2. Рассчитываем токи в ветвях методом узловых потенциалов. Потенциал четвертого узла принимаем равным нулю: 5.2.1. Составляем уравнение для определения потенциала
5.2.1.1. Подставляем числовые значения и находим потенциал 5.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
Узловые токи
5.2.1.3. После подстановки цифровых значений, определяем потенциал 5.2.2. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.100.
5.2.3. Используя второй закон Кирхгофа, определяем токи
Токи в ветвях, рассчитанные в примерах 2.3 и 2.25 совпадают.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.008 с.) |


 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  , а также параллельно соединенные
, а также параллельно соединенные  и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
: Ом,
Ом,  Ом.
Ом.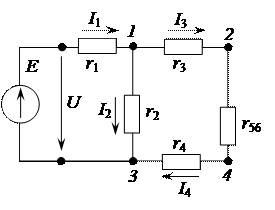
 ,
,  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 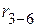 :
: Ом.
Ом.
 :
: Ом.
Ом.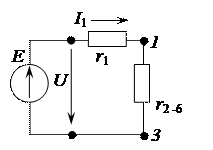
 Ом.
Ом. А.
А. ,
,  и
и  . Для их определения необходимо предварительно определить напряжение
. Для их определения необходимо предварительно определить напряжение 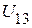 (рис. 2.85).
(рис. 2.85). В, или
В, или В.
В. А;
А; А, или
А, или А.
А. и
и  . Для их определения необходимо предварительно определить напряжение
. Для их определения необходимо предварительно определить напряжение  (рис. 2.83).
(рис. 2.83). В, или
В, или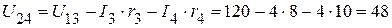 В.
В. А;
А; А, или
А, или А.
А. Вт.
Вт. Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.
 и
и  :
: Ом,
Ом,  Ом.
Ом.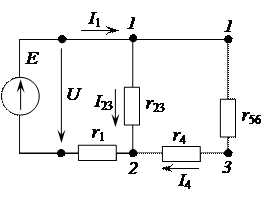
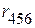 :
: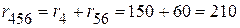 Ом.
Ом.
 Ом.
Ом.
 Ом.
Ом. мА.
мА. .
. В, или
В, или В.
В. мА;
мА; мА,
мА, мА, или
мА, или мА.
мА. В, или
В, или В.
В.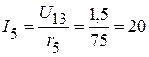 мА;
мА; мА, или
мА, или мА.
мА. Вт.
Вт. Вт,
Вт,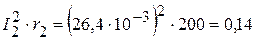 Вт,
Вт,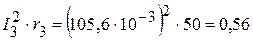 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
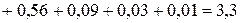 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.

 и внутреннним сопротивлением rв можно заменить параллельным соединением источника тока
и внутреннним сопротивлением rв можно заменить параллельным соединением источника тока  с внутренней проводимостью gв. Ток источника тока равен:
с внутренней проводимостью gв. Ток источника тока равен: А.
А. См.
См.
 А.
А. В.
В. Вт.
Вт. Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%. В.
В. А, или
А, или А.
А. Вт.
Вт.
 . По первому закону Кирхгофа соотношения выполняются, второй закон Кирхгофа мы не изменяли.
. По первому закону Кирхгофа соотношения выполняются, второй закон Кирхгофа мы не изменяли. ,
,  ,
,  .
.
 , количество узлов –
, количество узлов –  .
.
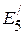 и
и  , которые соответственно равны:
, которые соответственно равны: В,
В, В.
В.

 Ом,
Ом,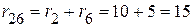 Ом,
Ом,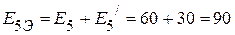 В,
В, В.
В. , количество узлов –
, количество узлов –  .
. . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал  .
. .
.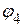 .
. См;
См; А.
А. В.
В. А,
А, А,
А, А.
А. А;
А; А.
А.


