
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Даниила Бернулли для потока реальной жидкости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Энергетический баланс потока жидкости определяется уравнением Даниила Бернулли, впервые выведенным им в 1738 г. для элементарной струйки идеальной жидкости (т.е. не имеющей вязкости) при установившемся движении. В последующем на основании работ как Д.Бернулли, так и других ученых (Л. Эйлера, Г. Кориолиса, Ж. Буссинеска и др.), это уравнение было сформировано для целого потока реальной жидкости, однако в истории науки оно известно как уравнение Даниила Бернулли. Для составления энергетического баланса рассмотрим поток, проходящий по трубопроводу переменного сечения от живого сечения
 
Рис. 25. Графическое изображение уравнения Д. Бернулли для потока реальной жидкости при установившемся движении: 1 - поток; 2 - пьезометр; 3 - трубка Пито; 4 - линия полной энергии;
Рассмотрим полную удельную энергию в сечениях относительно плоскости сравнения Полная удельная энергия потока в сечении
Полная удельная энергия потока в сечении
Показания пьезометров и скоростных трубок, установленных в сечениях Это вызвано тем, что часть энергии потока расходуется на преодоление гидравлических сопротивлений при движении жидкости от одного сечения к другому. Величина
Полученное выражение и называется уравнением Бернулли для потока реальной жидкости. Влияние вязкости жидкости приводит к неравномерному распределению скоростей в поперечном сечении потока (трубопровода). Поэтому уравнение (72) перепишется в следующем виде:
где
При равномерном движении воды в трубах и каналах небольшого поперечного сечения коэффициент Кориолиса принимается равным 1,05….1,1. В большинстве случаев при практических расчетах полагают Каждая составляющая уравнения Бернулли имеет геометрический и энергетический смысл. Все члены уравнения (73) имеют линейную размерность, и каждый из них может называться высотой:
Сформулируем геометрический смысл уравнения Бернулли для потока реальной жидкости.
При установившемся потоке реальной жидкости сумма четырех высот (высота положения, пьезометрическая высота, высота скоростного напора и высота потерь напора) есть величина постоянная для любого сечения потока. Энергетический смысл уравнения Бернулли заключается в следующем: при установившемся потоке реальной жидкости сумма четырех удельных энергий (энергии положения, энергии давления, кинетической энергии и энергии потерь) остается неизменной для любого сечения потока. Уравнение Бернулли является основным уравнение гидродинамики, с помощью которого выводятся расчетные формулы для различных случаев движения жидкости, и решается большое количество практических задач равномерного движения жидкости в трубах и открытых руслах. Для решения этих задач используют два основных уравнения гидродинамики: 1) уравнение Бернулли
2) уравнение неразрывности потока
При решении задач обычно по длине потока выбирают два характерных поперечных сечения ( Взаимосвязь между тремя параметрами: скоростью, давлением и живым сечением послужила основой для конструирования различных гидравлических и пневматических машин, устройств и приспособлений, получивших широкое применение в технике.
Примеры практического применения уравнения Д. Бернулли Трубы Вентури Уравнение Д. Бернулли является основным законом установившегося движения жидкости. Оно позволяет рассмотреть и понять работу ряда устройств, действие которых основано на использовании этого важнейшего закона. Рассмотрим некоторые из устройств: трубы Вентури, гидродинамические трубки, насосы и карбюраторы. Трубы Вентури предназначены для измерения расхода жидкости в напорных трубопроводах (рис. 26). Труба Вентури состоит из входного цилиндрического патрубка 1, входного конуса (конфузора) 5, цилиндрической горловины 6 и длинного диффузора 7. Для отбора давления к кольцевым камерам 2 и 8 присоединяются пьезометры 3 и 4. В свою очередь кольцевые камеры сообщаются с потоком жидкости через ряд отверстий 9, выполненных по окружности. В качестве сужающих устройств для измерения расхода в напорных трубопроводах кроме труб Вентури используются диафрагмы и сопла.

Рис. 26. Схема трубы Вентури: 1 - входной патрубок; 2, 8 - входной патрубок; 3 - пьезометр №1; 4 - пьезометр №2; 5 - входной конус (конфузор); 6 - горловина; 7 - диффузор; 9 - отверстие для отбора давления;
При выборе типа сужающего устройства надо иметь в виду, что наибольшее гидравлическое сопротивление имеет диафрагма, а наименьшее – труба Вентури. Перепад давления в сужающих устройствах в производственных условиях измеряется обычно дифференциальными ртутными манометрами, а в лабораторных - пьезометрами. Метод измерения расхода основан на том, что поток жидкости, протекающей в трубопроводе, неразрывен и, если в одном месте трубы с помощью какого-либо сужающего устройства уменьшить поперечное сечение, то скорость потока на этом участке должна соответственно увеличиться. Полная энергия жидкости, представляющая собой сумму потенциальной энергии (выраженной величиной давления), и кинетической энергии (выраженной величиной скорости), является, согласно закону сохранения энергии, постоянной, если пренебречь потерями. Тогда при протекании жидкости происходит частичный переход потенциальной энергии в кинетическую. В связи с этим статическое давление в суженном сечении будет меньше давления перед местом сужения. Разность давлений перед суженным участком трубопровода и в месте его сужения называется перепадом давления. Перепад давления тем больше, чем больше скорость жидкости. Следовательно, перепад давления может служить мерой расхода жидкости. Зависимость между расходом
Примем, что плоскость сравнения
Из полученного уравнения (76) следует, что с увеличением скорости движения давление уменьшается и, наоборот, с уменьшением скорости давление увеличивается. Это положение и используется в водомере Вентури, где по разности показаний пьезометров Выражение (76) можно переписать в следующем виде:
где Из уравнения неразрывности потока следует, что
Отсюда
Тогда
Или
где
Следовательно, зная разность показаний пьезометров, можно определить расход напорного потока жидкости. Если учесть потери энергии, которыми мы пренебрегали в начальный период, то в полученную формулу (79) следует ввести коэффициент расхода Окончательно формулу (79) перепишем в виде
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.183 (0.008 с.) |

 к живому сечению
к живому сечению 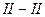 (рис. 25).
(рис. 25).

 - плоскость сравнения.
- плоскость сравнения. (70)
(70) , (71)
, (71)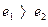 .
. называется удельной потерей энергии (или потерей напора) и обозначается
называется удельной потерей энергии (или потерей напора) и обозначается 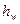 . Отсюда на основании закона сохранения энергии запишем следующее уравнение
. Отсюда на основании закона сохранения энергии запишем следующее уравнение (72)
(72) , (73)
, (73)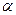 - коэффициент, характеризующий неравномерность распределения скоростей (коэффициент Кориолиса).
- коэффициент, характеризующий неравномерность распределения скоростей (коэффициент Кориолиса).
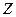

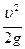

 , (75)
, (75)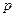 и
и  , а для другого – одна или две из них были неизвестны и подлежали определению.
, а для другого – одна или две из них были неизвестны и подлежали определению.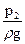
 - длина участков;
- длина участков;  и
и 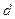 - диаметры.
- диаметры.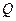 и перепадом давления
и перепадом давления  можно установить, пользуясь уравнением Бернулли. Для этого выберем на рис. 26 два сечения: сечение
можно установить, пользуясь уравнением Бернулли. Для этого выберем на рис. 26 два сечения: сечение 
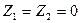 ). Пренебрегая величиной потерь напора,
). Пренебрегая величиной потерь напора,  , и неравномерностью распределения скоростей в потоке
, и неравномерностью распределения скоростей в потоке  , для горизонтально установленного водомера уравнение Бернулли (74) запишем в следующем виде:
, для горизонтально установленного водомера уравнение Бернулли (74) запишем в следующем виде: , (76)
, (76) (77)
(77) , (78)
, (78) ,
,  . Подставив значения
. Подставив значения  и
и  в выражение (77), получим
в выражение (77), получим
 .
. , (79)
, (79) - постоянная водомера заданной конструкции и размеров.
- постоянная водомера заданной конструкции и размеров.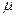 , учитывающий эти потери;
, учитывающий эти потери;  .
. . (80)
. (80)


