
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Режимы движения вязкой жидкости. Число Рейнольдса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Скорость и расход жидкости при ламинарном режиме. Установившееся движение жидкости является равномерным, если при этом живое сечение, скорость течения и глубина остаются постоянными по длине потока. Такое движение жидкости подчиняется основным законам динамики и является предпочтительным при проектировании различных гидравлических течений. Основное уравнение равномерного движения жидкости выглядит так:
Среднюю скорость установившегося равномерного движения определяют по формуле Шези:
где С - коэффициент Шези, Расход жидкости при равномерном движении жидкости определяют из выражения:
где
Режимы движения жидкости. Рядом исследователей еще в первой половине XIX века было замечено, что в потоке жидкости его частицы могут совершать движение по принципиально различным траекториям, и в соответствии с этим появилось понятие о существовании различных «режимов движения» жидкости. В 1839-1854 г.г. немецким инженером-гидротехником Г. Хагеном было открыто существование двух принципиально разных режимов движения жидкости. В 1880 г. этот вопрос рассматривал Д.И. Менделеев. Определенная ясность в этот вопрос была внесена английским физиком и инженером Осборном Рейнольдсом, который в 1883 г. опубликовал результаты своих наблюдений на лабораторной установке за водой, движущейся с различными скоростями в стеклянной трубке. Опыты показали, что при малых скоростях движения воды, подкрашенная жидкость в виде тонкой струйки внутри ее не перемешивается с основным потоком. Такой режим получил название ламинарного (от латинского слова lamina, означающего слой, полоска). После достижения определенной для данных условий опыта средней скорости движения, когда движение частиц жидкости приобретает как бы беспорядочный характер, струйка краски начинает размываться, отчего вся вода по сечению трубки окрашивается. Этот режим получил название турбулентного (от латинского слова turbulentus, означающего беспорядочный). Опыты позволили установить, что режим движения зависит не только от скорости Рейнольдс установил, что критерием режима движения жидкости является безразмерная величина, которая впоследствии была названа его именем – числом Рейнольдса Для труб цилиндрического сечения число Рейнольдса определяется по формуле
где
Критерий режима движения, соответствующий нижней критической скорости, называют нижним критическим числом Рейнольдса. На основании экспериментальных опытов установлено, что нижнее критическое число Рейнольдса для труб при напорном движении С физической точки зрения критерий Рейнольдса есть отношение сил инерции потока к силам трения при его движении. Определение режима движения жидкости в практических расчетах имеет очень важное значение. Опыты показали, что потери напора по длине потока при ламинарном режиме движения пропорциональны средне скорости течения в первой степени:
Для турбулентного режима движения потери напора по длине потока пропорциональны средней скорости течения в степени
Экспериментальными исследованиями было установлено, что при турбулентном режиме движения жидкости основную часть потока по сечению составляет турбулентное ядро, а около стенок трубы существует пограничный слой, состоящий из тонкого ламинарного и тонкого переходного слоев (рис. 31). Толщина ламинарного слоя
Стенки труб имеют шероховатость. В зависимости от соотношения ламинарного слоя
Рис. 31. Структура турбулентного потока: а – пограничные слои; б – гидравлически гладкая труба; в – гидравлически шероховатая труба; 1 – ламинарный слой; 2 – переходный слой; 3 – турбулентное ядро; шероховатость;
Так как фактическая высота всех выступов шероховатости не является одинаковой, то вводится понятие эквивалентной шероховатости, которая обозначается или Шероховатость обычно характеризуется не высотой выступов шероховатости Следует заметить, что при различных числах Рейнольдса одна и та же труба может быть как гладкой, так и шероховатой. Ниже приведены численные значения эквивалентной шероховатости для некоторых поверхностей,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 984; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

 (83)
(83)
 ;
;

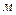 ;
;

 .
.
 ,
,  . (84)
. (84) (Приложение 7).
(Приложение 7). ,
,  , (85)
, (85)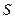 - площадь живого сечения потока,
- площадь живого сечения потока, 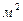 .
. , но и от вязкости
, но и от вязкости 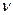 и диаметра трубы d.
и диаметра трубы d.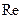 .
. , (86)
, (86) .
.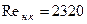 . По критическому числу устанавливают вид режима движения жидкости. Так если
. По критическому числу устанавливают вид режима движения жидкости. Так если 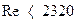 , то поток будет иметь ламинарный режим движения, так как
, то поток будет иметь ламинарный режим движения, так как  и режим находится в ламинарной зоне. Если же
и режим находится в ламинарной зоне. Если же  , то поток находится в зоне неустойчивого движения (зона переходного режима), до значения
, то поток находится в зоне неустойчивого движения (зона переходного режима), до значения  . Далее следует зона устойчивого турбулентного течения.
. Далее следует зона устойчивого турбулентного течения.


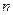 :
:

 определяется по формуле
определяется по формуле , (87)
, (87)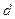
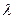
 : различают гидравлически гладкие трубы, если
: различают гидравлически гладкие трубы, если  (рис. 31, б) и гидравлически шероховатые, если
(рис. 31, б) и гидравлически шероховатые, если 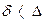 (рис. 31, в).
(рис. 31, в).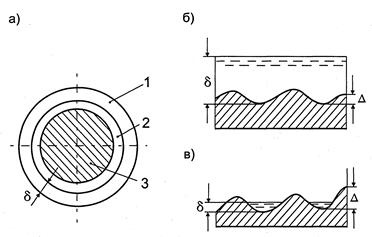
 или
или  , т.е. такая равномерная шероховатость, которая дает при подсчете одинаковую с заданной шероховатостью величину потерь напора по длине
, т.е. такая равномерная шероховатость, которая дает при подсчете одинаковую с заданной шероховатостью величину потерь напора по длине 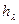 .
. или
или  , и называется относительной шероховатостью.
, и называется относительной шероховатостью. .
.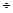 1,0
1,0



