
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение жидкости при переменном напореСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Величина напора и скорости соответственно меняются, мы имеем неустановившееся движение жидкости. Рассмотрим самый простой случай опорожнения или наполнения призматического резервуара.
Рис. 55. Схема расчета при параллельном напоре
На дне резервуара имеется отверстие площадью
За этот же отрезок времени уровень жидкости понизится на величину
решая это уравнение относительно
интеграл и
При полном опорожнении резервуара при
При постоянном напоре
Гидравлические струи Гидравлическая струя - конечный поток жидкости, не ограниченный твердыми стенками. Бывают затопленными и незатопленными. Струя, вытекающая в однородную жидкость, называется затопленной; в атмосферу - незатопленной (брандспойт, для разработки грунта). Незатопленная струя, вытекающая из насадка с цилиндрическим отверстием в атмосферу, имеет следующую структуру по длине:
Рис. 56. Схема струи
В компактной части струи обеспечивается сплошность потока, струя имеет правильную цилиндрическую форму. В раздробленной Для разработки грунтов, добычи угля, воздействия на лопатки активной гидравлической турбины требуется струя с хорошо развитой компактной частью Для определения осевой скорости струи в пределах её компактной части существует формула Н. П. Гавырина:
Для определения дальности полета струи пользуются экспериментальной формулой Н. П. Гавырина
Расчет турбин Рассмотрим воздействие гидравлической струи на неподвижную преграду. Предположим, что струя вытекает из сопла со средней скоростью и встречает на своем пути неподвижную вертикальную стенку. Если вертикальная стенка плоская, то струя ударяясь о нее, растекается во все стороны. Для того, чтобы струя растекалась при встрече лишь по двум направлениям, сделаем в вертикальной стене направляющий желоб, попав в который струя после удара разделится на верхнюю и нижнюю части. Пусть струя имеет в сечении 1 - 1 площадь живого сечения При встрече со стенкой струя разделится на две части: Выделим отсек струи 1- 2 - 3. За время
Рис. 57. Схема разделения струи.
Применим к движению отсека теорему количества движения, которая звучит: изменение проекции количества движения на заданную ось за время
Из рисунка видно, что
где
тогда уравнение (183) будет таким:
откуда сила воздействия струи на вертикальную стенку будет:
Если стенка находится под некоторым углом к струе, то
Мощность струи, действующей на подвижную преграду (лопатку турбины), определим так: пусть плоская лопатка движется со скоростью vл, тогда
где
Максимальное значение мощности можно получить при
Т.е. максимальная теоретическая мощность турбины с плоскими лопатками равна половине полной кинетической энергии струи. В действительности потери энергии составляют 40-45%. Если применить криволинейные лопатки в виде ковшей, то при
Лекция 10.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.009 с.) |

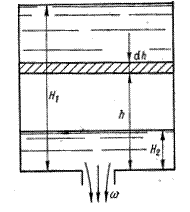
 , а площадь резервуара -
, а площадь резервуара -  . Необходимо определить время уменьшения уровня от
. Необходимо определить время уменьшения уровня от  до
до  . Очевидно, что за бесконечно малый промежуток времени
. Очевидно, что за бесконечно малый промежуток времени  и напор
и напор  можно считать постоянным. И количество жидкости, вытекающее через отверстие
можно считать постоянным. И количество жидкости, вытекающее через отверстие 
 , а объем жидкости уменьшится на величину
, а объем жидкости уменьшится на величину  , следовательно:
, следовательно: (175)
(175) (176)
(176) ;
; (177)
(177) ,
, или
или 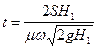 (178)
(178) будет вытекать за время
будет вытекать за время (179)
(179)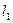 - компактная,
- компактная,  - раздробленная,
- раздробленная,  - распыленная часть струи.
- распыленная часть струи.
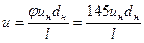 (180)
(180)
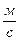 ;
;

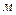 ;
;
 - коэффициент.
- коэффициент.
 (181)
(181)
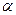
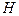
 . Расход
. Расход  до встречи со стенкой.
до встречи со стенкой. и
и 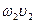 . Очевидно, что
. Очевидно, что  принимаем
принимаем  и
и  .
.
 (182)
(182)
 ,
,  - количество движения объемов жидкости, заключенных между сечениями 2 - 2; 2¢ - 2¢; 3¢ - 3¢;
- количество движения объемов жидкости, заключенных между сечениями 2 - 2; 2¢ - 2¢; 3¢ - 3¢;


 ).
).
 , а
, а  . И уравнение примет вид:
. И уравнение примет вид: (183)
(183)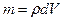 ;
; - элементарный объем струи между сечениями 1 - 1 и 1¢ - 1¢, т.е.
- элементарный объем струи между сечениями 1 - 1 и 1¢ - 1¢, т.е. 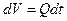 ,
, (184)
(184) , (185)
, (185) (186)
(186) ,
, ,
, - скорость лопатки,
- скорость лопатки,  :
: (187)
(187) и
и 




