
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы трения и закон распределения скоростей при ламинарном и турбулентном режимах движения жидкости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При ламинарном режиме движения жидкости в трубе в ней возникают силы трения и она начинает двигаться как бы цилиндрическими бесконечно тонкими слоями с различными скоростями. Скорости слоев жидкости от продольной оси трубопровода к ее стенкам уменьшаются по параболическому закону. На оси трубы они имеют максимальное значение. На поверхности стенок трубы скорость течения равна нулю. Слои жидкости, движущиеся с меньшей скоростью тормозят движение слоев, имеющих большую скорость. Цилиндрические слои жидкости, движущиеся с большей скоростью, скользят по слоям жидкости, движущимся с меньшей скоростью. На поверхностях смежных слоев жидкости благодаря наличию сцепления частиц жидкости между собой и со стенками, ограждающими поток, в процессе скольжения развиваются силы трения. Силы трения, появившиеся на граничащих поверхностях между слоями жидкости, осуществляют тормозящее действие, что и приводит к возникновению разных скоростей движения отдельных частиц жидкости. Главной причиной возникновения сил трения при движении потока следует считать разность скоростей между движущимися слоями жидкости. Чем больше разность скоростей, тем больше по величине возникающие силы трения, силы гидравлических сопротивлений. Рассмотрим ламинарный режим движения в цилиндрической трубе (рис. 32). В модели такое движение можно представить состоящим из множества телескопически выдвинутых цилиндров толщиной
Рис. 32. Эпюра скоростей при ламинарном режиме движения
Касательное напряжение
При направлении координатных осей
Знак минус потому, что здесь при После подстановки в уравнение равномерного движения получим дифференциальное уравнение распределения скорости в таком виде:
Проинтегрировав, найдем
Определим постоянную интегрирования С по условиям на границе. В точке у стенки трубы
Следовательно, уравнение примет вид:
или окончательно
Тогда расход потока в трубе
Разделив (88) на
Следовательно, средняя скорость равна половине максимальной. Потерянный напор найдем из (90), учитывая, что
Умножив и разделив правую часть на
Но
или, обозначив
Формула (91), как известно, называется формулой Дарси-Вейсбаха. Здесь
Турбулентное движение.
Турбулентное состояние потока характеризуется непрерывным перемешиванием множества мельчайших водоворотных образований, возникающих у твердых границ и перемещающихся внутрь потока. Зарождение водоворотных образований обязано вязкости жидкости. На поверхности контакта жидкости и твердых стенок молекулы жидкости и молекулы твердых стенок находятся на расстоянии силового их взаимодействия. В связи с этим частицы жидкости непосредственно у стенок задерживаются, и скорость их равна нулю. Соседние с ними частицы приходят в движение, и их скорость возрастает с удалением от стенок. При этом возникает вращательное движение отдельных масс жидкости. Сложение двух движений - поступательного и вращательного - возбуждает силу, приложенную к массе частицы и направленную нормально к продольной скорости потока (эффект Магнуса). Под действием этой силы частицы жидкости перемещаются в центральную область потока, образуя процесс перемешивания. Наличие шероховатости стенок содействует такому перемешиванию и в некоторых случаях может оказаться даже главной причиной явления. Этот процесс, очевидно, возможен при достаточно больших скоростях течения, при которых стабилизирующее воздействие вязкости не может воспрепятствовать такому перемешиванию. Известно, что турбулентное движение возникает при скоростях больше Процесс перемешивания обуславливает возникновение пульсации скоростей, т.е. такое изменение ее величины в данной точке, при котором отклонения от некоторой средней происходят в обе стороны. Объясняется это тем, что через данную точку пространства последовательно проходят разные частицы жидкости с разными скоростями как по величине, так и по направлению. Обычно наибольшее внимание уделяется явлению пульсации продольной скорости В связи с явлением пульсации турбулентное движение оказывается неустановившимся, и в любой момент времени имеет место мгновенное поле скоростей (и других кинематических параметров потока). При этом возможно говорить о средних значениях скорости за тот или иной промежуток времени. Чем больше промежуток времени осреднения, тем точнее определяется данная величина. Определенная таким образом скорость называется осредненной скоростью в данной точке. Связь между мгновенной и осредненной скоростью определяется так:
где Процесс перемешивания вызывает перенос количества движения из области малых скоростей потока в область больших скоростей и обратно. Очевидно, массы с малыми скоростями при входе в область течений с большими скоростями будут тормозить движение в этой области, т.е оказывать силовое противодействие движению. Это будут силы инерции, и, следовательно, физическая природа турбулентных сопротивлений – инерционная. Масса жидкости с большими скоростями, оказывая давление на присоединенные массы, ускоряют их движение и расходуют при этом свою энергию (при этом ускорении возникают силы инерции). Прандтль при установлении закона распределения скоростей принял следующую схему течений в трубопроводе. У стенок трубы скорости принимаются нулевыми, к центру (оси трубы) они постепенно увеличиваются, т.е. у стенок трубы создается ламинарный слой небольшой толщины, за пределами которого располагается центральная основная часть потока – турбулентное ядро. В связи с малыми скоростями течения в ламинарном (пристенном) слое скорости быстро нарастают, градиент скорости здесь велик, и его можно приближенно считать величиной постоянной. В пределах центрального ядра турбулентное течение и изменение скоростей происходят не так интенсивно. Иллюстрация такой схемы показана на рис. 33. Для ламинарного режима касательные напряжения определяются по формуле Ньютона
Рис. 33. Эпюра скоростей при турбулентном режиме движения
При турбулентном режиме движении
где По данным исследований Г.А. Гуржиенко, вблизи стенок трубы зависимость
где По Г.А. Гуржиенко, Благодаря пульсации в турбулентном потоке жидкости закон распределения скоростей по живому сечению иной, чем при ламинарном. При турбулентном движении происходит выравнивание скоростей по сечению. Для развитого турбулентного режима движения жидкости ввиду малой ее массы, участвующей в пограничном слое, первый член правой части уравнения (92) по сравнению со вторым членом является малой величиной. поэтому им можно пренебречь. Тогда уравнение (92) будет иметь вид
Или
Подставляя значение
где Примем
Лекция 7 Классификация потерь напора Одним из важнейших вопросов гидромеханики является определение потерь энергии при движении жидкости. При движении жидкости по трубопроводам возникают потери энергии, которые зависят от длины трубопроводов (пропорциональные длине канала) и потери энергии в местных сопротивлениях – запорная арматура, повороты, расширения и сужения трубопроводов – вызываемые изменениями скорости потока либо по величине, либо по направлению. Потери энергии потока как на преодоление сопротивлений по длине трубопроводов, так и на преодоление местных сопротивлений, в конечном счете обусловлены вязкостью жидкости, а, следовательно, теряемая механическая энергия рассеивается и переходит в тепловую. Важность определения потерь напора Потерянный напор является суммой двух слагаемых:
где Для вычисления потерь напора при турбулентном режиме обычно пользуются частными эмпирическими формулами
и
Средняя скорость, входящая в формулы (99) и (100) – эта такая, одинаковая для всех точек сечения скорость, при которой за единицу времени через данное сечение проходит тот же расход жидкости, что и при действительном распределении скоростей по сечению потока. Среднюю скорость определяют по уравнению расхода
Из формул (99) и (100) следует, что потери энергии на трение и местные сопротивления пропорциональны скоростному и динамическому напору ( Величина коэффициента трения проявляется по-разному при различных режимах движения потока в трубе. В одном диапазоне чисел Рейнольдса, характеризующих режим движения, на величину В связи с этим различают четыре области сопротивления, в которых изменение Первая область – область ламинарного потока, ограниченная значениями
При этом значении Вторая область – гидравлически гладкие трубы. Поток в трубе при этом турбулентный, но у стенок трубы сохраняется слой жидкости, в пределах которого движение остается ламинарным. Трубы считаются гидравлически гладкими, если толщина ламинарного слоя Границу зоны гидравлически гладких труб можно определить из зависимости:
Для гидравлически гладких труб, т.е при условии
которая применима при значениях чисел Рейнольдса Третья область – переходная от области гидравлически гладких труб к квадратичной области. В этой области толщина ламинарного слоя Для определения
Потери напора по длине трубы в переходной области сопротивления пропорциональны скорости в степени от Четвертая область – гидравлически шероховатых труб или квадратичного сопротивления (автомодельная область). Основное влияние на сопротивление потоку оказывает шероховатость стенок трубы. Чем больше выступы шероховатости
Для автомодельной области в уравнении (105) можно пренебречь вторым слагаемым в квадратных скобках, и оно принимает вид
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.14 (0.01 с.) |

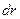 . Огибающую этих цилиндров можно рассматривать как эпюру скоростей струек.
. Огибающую этих цилиндров можно рассматривать как эпюру скоростей струек.
 на боковой поверхности выделенного цилиндра определим в соответствии с законом Ньютона о силе сопротивления в жидкости, а именно
на боковой поверхности выделенного цилиндра определим в соответствии с законом Ньютона о силе сопротивления в жидкости, а именно
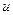 и
и 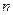 , указанном на рис. 32 – ось скорости
, указанном на рис. 32 – ось скорости  , можем записать:
, можем записать:
 имеем
имеем  .
.

 , т.е. радиусу трубы, а скорость
, т.е. радиусу трубы, а скорость  . Тогда
. Тогда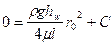 и
и 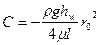

 (88)
(88) (89)
(89) , найдем среднюю скорость
, найдем среднюю скорость (90)
(90) :
: .
. и затем преобразовав, получим:
и затем преобразовав, получим: .
. , тогда
, тогда
 ,
, . (91)
. (91)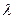 - коэффициент гидравлического сопротивления в трубах. Как видно, при ламинарном движении коэффициент
- коэффициент гидравлического сопротивления в трубах. Как видно, при ламинарном движении коэффициент  (когда число Рейнольдса больше
(когда число Рейнольдса больше  ).
). , измеряемой в точке поперечного сечения с помощью различных гидрометрических приборов.
, измеряемой в точке поперечного сечения с помощью различных гидрометрических приборов. ,
, ,
, 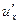 - соответственно мгновенная, осредненная и пульсационная составляющие скорости.
- соответственно мгновенная, осредненная и пульсационная составляющие скорости.

 . (92)
. (92)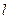 - путь перемешивания, аналогичен средней длине пробега молекул в кинетической теории газов.
- путь перемешивания, аналогичен средней длине пробега молекул в кинетической теории газов.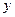 оказалась линейной, поэтому можно написать
оказалась линейной, поэтому можно написать (93)
(93) - коэффициент пропорциональности, называемый универсальной постоянной.
- коэффициент пропорциональности, называемый универсальной постоянной.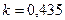 . Следовательно,
. Следовательно,  . Первый член
. Первый член  характеризует вязкостное трение, которое соответствует силам трения в ламинарном движении. Второй член
характеризует вязкостное трение, которое соответствует силам трения в ламинарном движении. Второй член  выражает дополнительное касательное напряжение от пульсации, возникающей в турбулентном потоке из-за наличия поперечного движения отдельных частиц жидкости. С увеличением скорости течения (числа Рейнольдса) главное влияние на величину касательных напряжений оказывает второй член в уравнении (92) и при больших числах Рейнольдса касательные напряжения оказываются пропорциональными квадрату градиента скорости.
выражает дополнительное касательное напряжение от пульсации, возникающей в турбулентном потоке из-за наличия поперечного движения отдельных частиц жидкости. С увеличением скорости течения (числа Рейнольдса) главное влияние на величину касательных напряжений оказывает второй член в уравнении (92) и при больших числах Рейнольдса касательные напряжения оказываются пропорциональными квадрату градиента скорости. (94)
(94) (95)
(95) , будем иметь
, будем иметь , (96)
, (96) - называется динамической скоростью, так как имеет размерность скорости.
- называется динамической скоростью, так как имеет размерность скорости. , тогда после интегрирования дифференциального уравнения (96) получим логарифмический закон распределения скоростей по сечению для турбулентного потока:
, тогда после интегрирования дифференциального уравнения (96) получим логарифмический закон распределения скоростей по сечению для турбулентного потока: . (97)
. (97)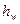 (или потерь давления
(или потерь давления  ) связана с необходимостью расчета затрат энергии, требуемых для компенсации этих потерь при перемешивании жидкостей, например, с помощью насосов, компрессоров и т.д.
) связана с необходимостью расчета затрат энергии, требуемых для компенсации этих потерь при перемешивании жидкостей, например, с помощью насосов, компрессоров и т.д. (98)
(98)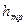 ,
, 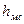 - потери напора вследствие трения и местных сопротивлений, соответственно.
- потери напора вследствие трения и местных сопротивлений, соответственно. (99)
(99) (100)
(100)
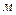 ;
;
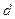

 ;
;
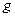
 .
.
 (101)
(101)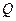
 ;
;
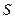
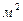 .
.
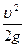 ), который является мерой кинетической энергии потока, отнесенной к единице объема жидкости. В действительности эта зависимость значительно сложнее, так как коэффициент трения и коэффициент местного сопротивления не являются постоянными величинами, а существенно зависят от скорости течения жидкости, ее плотности и вязкости, а также диаметра и шероховатости трубы, по которой движется поток.
), который является мерой кинетической энергии потока, отнесенной к единице объема жидкости. В действительности эта зависимость значительно сложнее, так как коэффициент трения и коэффициент местного сопротивления не являются постоянными величинами, а существенно зависят от скорости течения жидкости, ее плотности и вязкости, а также диаметра и шероховатости трубы, по которой движется поток. ).
). , в которой
, в которой 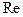 и не зависит от величины
и не зависит от величины  больше высоты выступов шероховатости
больше высоты выступов шероховатости  (103)
(103) коэффициент
коэффициент  , (104)
, (104) .
. (105)
(105) до
до  .
. , выражаемой отношением абсолютной шероховатости
, выражаемой отношением абсолютной шероховатости  (106)
(106) . (107)
. (107)


