Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения теории внутреннего трения в жидкостяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2.1. Основные определения Жидкостями называются вещества, имеющие определённый объем, но не обладающие упругостью формы (то есть, не обладающие модулем сдвига). В отличие от твердых тел в жидкостях наблюдается ближний порядок (упорядоченное расположение соседних атомов или молекул на расстояниях порядка их нескольких межмолекулярных расстояний); дальний же порядок, присущий твердым телам (кристаллическая решетка) и вовсе отсутствует. Временем “оседлой жизни” называется время, в течение которого молекулы жидкости сохраняют свое местоположение. По истечении данного времени, молекулы жидкости перемещаются на расстояния порядка 10-8 см. Молекулы жидкости, подобно молекулам твердых тел, совершают тепловые колебания около положений равновесия. Текучесть – это способность молекул жидкости менять свое положение относительно других молекул. Вместе с тем, силы межмолекулярного взаимодействия достаточно велики и средние расстояния между молекулами остаются неизменными. По этой причине жидкости сохраняют свой объем. Явление внутреннего трения (вязкости) состоит во взаимодействии соседних слоев реальной жидкости, движущихся с разными скоростями, которое приводит к появлению сил вязкости (внутреннего трения), касательных поверхности слоев. При этом, молекулы более быстрого слоя стремятся увлечь за собой молекулы более медленного, и наоборот, молекулы более медленного слоя тормозят движение более быстрого. Следовательно, силы вязкости направлены вдоль поверхности соприкасающихся слоев в сторону, противоположную их относительной скорости подобно силам трения скольжения (внешнего трения) при движении одного тела по поверхности другого. По своей природе силы трения в жидкости являются силами межмолекулярного взаимодействия, то есть, электромагнитными силами, как и силы трения между твердыми телами. Явление вязкости, таким образом, связано с передачей импульса из слоя в слой, т.е. относится к явлениям переноса. Так как молекулы жидкости основную часть времени находятся около положения равновесия, то движущаяся масса жидкости увлекает соседние слои в основном за счет сцепления (межмолекулярного взаимодействия). С ростом температуры текучесть жидкости возрастает, а вязкость падает. Это связано с тем, что при нагревании жидкость “разрыхляется” (т.е. незначительно увеличивается ее объем) и силы межмолекулярного взаимодействия ослабевают. Механизм вязкости в газе является иным, так как осуществляется из-за перехода молекул из слоя в слой. Поэтому с возрастанием температуры вязкость газов, возрастает, в отличие от жидкостей.
Ламинарным называется такое течение, когда жидкие частицы движутся вдоль устойчивых траекторий. Жидкость движется параллельными слоями. Скорости всех частиц жидкости параллельны течению. Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не размываясь по всему потоку. Турбулентным течение становится при больших скоростях – это неустойчивое, хаотичное (вихреобразное) движение частиц жидкости. Установившимся или стационарным называется течение, если величины и направления скоростей частиц в каждой точке движущейся жидкости не изменяются со временем. 2.2. Закономерности движения реальной жидкости в цилиндрической трубе Пусть имеется жидкость, различные слои которой движутся с различными скоростями (рисунок 1), причем скорости слоев, отстоящих на расстоянии Δ y, отличаются на величину Δ v. Тогда отношение Δ v/ Δ y показывает, насколько быстро меняется скорость жидкости от одного слоя к другому. Для двух бесконечно близких слоев (Δ y ®0) эта величина записывается в виде dv/dy и представляет собой градиент скорости grad (v) в направлении перпендикулярном скорости движения слоев.
Рис.1. Схематическое изображение слоев. Ньютон впервые предположил, что сила вязкости или сила внутреннего трения dF в между двумя слоями жидкости прямо пропорциональна площади их соприкосновения dS τ, а также градиенту скорости:
Коэффициент пропорциональности h,зависящий от природы жидкости и ее температуры, называется коэффициентом вязкости или просто вязкостью. Коэффициент вязкости h измеряется в Па·с. Рассмотрим более подробно ламинарное течение жидкости по трубе круглого сечения радиуса R длиной l. Если разность давлений Δ P = P 1 – P 2 (P 1 > P 2) на концах трубы поддерживается постоянной, то установится стационарный режим течения, при котором за равные промежутки времени t через любое поперечное сечение трубы S будут протекать равные объемы жидкости V. Особенность течения вязкой жидкости по цилиндрической трубе состоит в том, что внешний слой жидкости, примыкающий к внутренней поверхности трубы, прилипает к ней и остается неподвижным, а скорость каждого из последующих слоев увеличивается по мере приближения к центру трубы. Течение жидкости можно представить в виде движения цилиндрических слоев, параллельных оси трубы. Мысленно выделим произвольную цилиндрическую область жидкости радиуса r и длины l (рисунок 2).
Рис.2. Схематическое изображение цилиндрической области жидкости. На ее боковую поверхность St =2 prl со стороны внешнего слоя, текущего с другой скоростью, действует, согласно (1), сила вязкости:
Кроме того, на основания цилиндра действует сила, связанная с разностью давлений:
При стационарном течении жидкости скорость движения жидкости постоянна, поэтому силы, действующие на цилиндрический слой, должны быть равны и противоположны по направлению FB = FP, следовательно
Выразим из этого уравнения dv и проинтегрируем получившееся выражение для того, чтобы найти скорость:
Пределы определенного интеграла выбраны из условия, что на стенке трубы (т.е. при r = R), скорость v должна обращаться в нуль. В результате получим
Таким образом, скорость частиц движущейся жидкости изменяется от максимального значения (на оси трубы) до нуля (на стенках трубы) по параболическому закону (рисунок 3).
Рис.3. Распределение скоростей слоев жидкости в трубе. Подсчитаем объем жидкости, протекающей через поперечное сечение трубы за время t. Для этого рассмотрим тонкий цилиндрический слой радиуса r, толщиной dr, текущий с постоянной скоростью v. За время t через кольцевую площадку площадью dS = 2 πrdr, которая представляет собой поперечное сечение этого тонкого слоя, протечет объем жидкости – dV = dS vt = 2 πrdr vt или, используя формулу (5),
Объем жидкости V, протекающей за время t через все поперечное сечение трубы S, находится путем интегрирования выражения (6) по r от 0 до R.
Разделив данное выражение на время t, получим объем жидкости, вытекающий из трубы за единицу времени или расход жидкости Q=V/t, а формула (7) будет иметь вид:
Формула (8) является количественным выражением закона Пуазейля. Из нее, в частности, следует, что расход жидкости обратно пропорционален длине трубы – l, и прямо пропорционален разности давлений на концах трубы и четвертой степени ее радиуса, то есть, чрезвычайно сильно возрастает с увеличением радиуса трубы. Если предположить, что все частицы жидкости движутся не с различными скоростями, а с некоторой средней скоростью v ср, то расход жидкости Q, то
Эксперименты показали, что закон Пуазейля оказывается справедливым лишь при относительно небольших скоростях движения жидкости. Осборн Ре΄йнольдс впервые заметил, что при достижении некоторой критической скорости движение жидкости теряет ламинарной характер и становится турбулентным (вихревым), то есть, струйка подкрашенной жидкости быстро расходится по всему сечению трубы в виде вихревых образований. Кроме того, было замечено, что значение критической скорости зависит также от размеров трубки и свойств самой жидкости. Так, например, если одна и та же жидкость течет по трубам различного диаметра, то в более широкой трубе переход от ламинарного течения к турбулентному будет происходить при меньших скоростях движения, чем в узкой. Таким образом, узкая труба оказывает более сильное, упорядочивающее влияние на характер движения жидкости. С другой стороны оказалось, что более вязкая жидкость сохраняет ламинарность течения при относительно более высоких скоростях движения.
Рейнольдс предложил характеризовать течение жидкости безразмерной величиной, названной числом Рейнольдса:
Здесь r и h - плотность и вязкость жидкости, v ср - средняя скорость ее течения, R – радиус трубы. Экспериментальные исследования показали, что ламинарный режим наблюдается при течениях, которым соответствуют значения чисел Рейнольдса не более ~1000. Переход от ламинарного к турбулентному течению происходит в области значений от 1000 до 2000, а при значениях Re > 2000 течение становится турбулентным.
Движение тел в жидкостях Силы вязкости проявляются и при движении различных тел в жидкости, которые действуют на боковую поверхность тела в направлении, противоположном скорости тела относительно жидкости. Силы вязкости пропорциональны первой степени скорости, коэффициенту вязкости h и линейным размерам тела l:
где k 1 – коэффициент пропорциональности. Если в жидкости движется шарик небольшого радиуса r с малой скоростью v, то сила сопротивления равна:
Эта формула впервые была получена Стоксом и носит его имя. Кроме того на тело, движущееся в жидкости, действуют силы лобового сопротивления. Действительно, тела, находящиеся в жидкости, действуют на частицы жидкости, изменяют характер потока, перераспределяют в нем скорости и давления до и после движущихся тел. Однако, эти же тела, согласно третьему закону Ньютона, испытывают такие же по величине, но противоположно направленные силы. Результирующая этих сил отлична от нуля и направлена в сторону, противоположную скорости тела относительно жидкости. Расчет показывает, что силы лобового сопротивления пропорциональны плотности жидкости ρ, площади поперечного сечения тела S и квадрату скорости v:
где k 2 – коэффициент, зависящий от формы тела, состояния его поверхности и от вязкости жидкости. Таким образом, и силы лобового сопротивления, и силы вязкости препятствуют движению тела в жидкости. При малых скоростях преобладают силы вязкости, пропорциональные первой степени скорости; при больших скоростях – силы лобового сопротивления, изменяющиеся по параболическому закону (рисунок 4).
Рис.4. Зависимость сил лобового сопротивления и вязкости от скорости движения тела в жидкости. Число Рейнольдса Re при движении тел в жидкости, как видно из формул (11) и (13), прямо пропорционально отношению FЛ / FB и показывает, какой вид сопротивления преобладает. При Re≤1 преобладают силы вязкости, при Re>1 – силы лобового сопротивления. При создании моделей тел, движущихся в жидкости, число Рейнольдса является критерием подобия. Характер движения модели будет такой же, как и моделируемого тела при условии совпадения их чисел Рейнольдса.
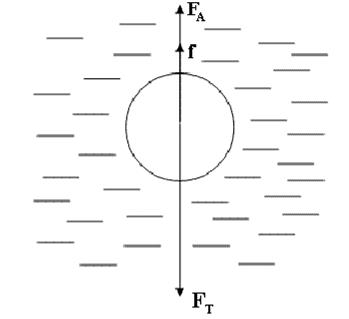
Методика выполнения работы 3.1. Определение вязкости жидкости методом Стокса Этот метод основан на исследовании условий движения шарика в вязкой жидкости. Размеры и плотность шарика выбираются такими, чтобы скорость его движения была невелика. В этом случае сила сопротивления определяется практически только вязкостью. Кроме силы вязкости f, на шарик, падающий в жидкости, действуют сила тяжести F T и сила Архимеда или выталкивающая сила F A (рисунок 5).
Рис.5. Схематическое изображение шарика в жидкости В начале движения F T > F A+ f и шарик движется ускоренно. При этом сила f, пропорциональная скорости шарика, увеличивается, пока равнодействующая всех этих сил не становится равной нулю и, далее, шарик движется в жидкости с постоянной скоростью v. Для этого случая запишем равенство F T = F A+ f. Перепишем его, используя формулу Стокса
где m ш – масса шарика; m ж – масса жидкости, вытесненной шариком; r – радиус шарика. Записав массу шарика и массу вытесненной им жидкости через плотности и объем, получим:
Отсюда
3.2. Определение числа Рейнольдса, соответствующего переходу от ламинарного течения жидкости к турбулентному Зависимость расхода жидкости в единицу времени от разности давлений Δ P = P 1 – P 2 на концах трубы вначале выражается линейной функцией в соответствии с формулой Пуазейля (пунктирная прямая на рисунке 6). При значениях Δ P, соответствующих числу Рейнольдса Re ~ 1000, происходит переход от ламинарного течения к турбулентному и отклонение зависимости Q = f (Δ P) от закона Пуазейля (точка “a” на кривой рисунка 6). При дальнейшем увеличении разности давлений наблюдается чисто турбулентный режим течения жидкости (отрезок “ab” на кривой рисунка 6).
Рис.6. Зависимость объема жидкости, вытекающей из трубы в единицу времени и числа Рейнольдса от разности давлений на концах трубы.
3.3. Описание лабораторной установки
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.17 (0.013 с.) |


 . (1)
. (1)
 . (2)
. (2) . (3)
. (3)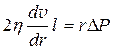 . (4)
. (4)
 . (5)
. (5)
 (6)
(6) (7)
(7) (8)
(8) . (9)
. (9) . (10)
. (10)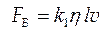 , (11)
, (11)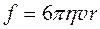 . (12)
. (12) ,(13)
,(13)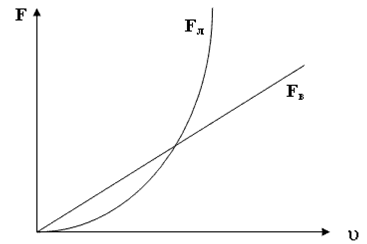
 , (14)
, (14) . (15)
. (15)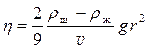 . (16)
. (16)