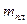Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное движение в открытых руслахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Равномерное движение потока жидкости – такое движение, при котором живые сечения, так же как и скорость потока в соответственных точках этих сечений, одинаковы по всей длине рассматриваемого участка. Типичным примером равномерного движения является движение в открытом канале или в цилиндрической трубе с одинаковыми по всей длине живыми сечениями. Для равномерного движения расход определяется по формуле
Скорость при равномерном движении выражается формулой
При гидравлическом расчете каналов вводится понятие расходной характеристики или модуля расход
Коэффициент С рекомендуется принимать по формуле академика Н.Н. Павловского
где n - коэффициент шероховатости, зависящий от материала и состояния русла; у - показатель степени, зависящий от гидравлического радиуса R и коэффициента шероховатости n.
Гидравлические параметры каналов. Формы поперечного сечения каналов бывают трапецеидальные, прямоугольные, треугольные, параболические и др. Для трапецеидального сечения русла (рис 58): - площадь живого сечения
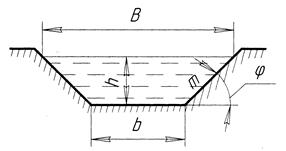
- коэффициент заложения откоса
где φ - угол линии откоса с горизонталью;
Рис. 58. Трапецеидальное сечение русла канала
- ширина живого сечения по верху
- смоченный периметр
где
- гидравлический радиус
Для прямоугольного сечения русла (рис. 59) - площадь живого сечения
- смоченный периметр
Рис. 59 Прямоугольное сечение русла канала
- гидравлический радиус
Для треугольного сечения русла (рис. 64)
- смоченный периметр
- гидравлический радиус
Рис. 60. Треугольное сечение русла канала
Для параболического сечения русла (рис. 61)
Рис. 61. Параболическое сечение русла канала - площадь живого сечения
ширина по верху
где
Таблица 7
Водосливы.
Классификация водосливов
Гидравлическое явление перелива потока жидкости через стенку или порог называют водосливом. Водосливом также называют стенку или порог, стоящие на пути движения потока жидкости. Теория водослива положена в основу теории расчета плотин, в том числе лесосплавных плотин, водопусков, подмостовых отверстий, малых гидросооружений для пропуска воды в дорожном полотне, в земляных дамбах. Кроме того, водослив может служить точным прибором для измерения скоростей и расходов. Акватория потока, расположенная выше водослива, называют верхним бьефом, ниже водослива - нижним бьефом. Водосливы по своему назначению можно подразделить на водосливы, которые предназначаются для поддержания горизонтов воды в водохранилищах и сброса расходов воды (например, водосливы с широким порогом или практического профиля), и на водосливы мерные, служащие для замера расхода жидкости (например, с трапецеидальным или треугольным отверстием). Водосливы также подразделяются: - по типу стенки (порога) – на водосливы с тонкой стенкой, практического профиля и с широким порогом; - по форме отверстия в стенке – на прямоугольные, треугольные, трапецеидальные, параболические и др.; - по типу сопряжения переливающейся струи с потоком нижнего бьефа – на незатопленные и затопленные; горизонт воды в нижнем бьефе в первом случае не оказывает влияния на истечение, во втором – влияет на истечение воды через водослив; - по очертанию в плане – на прямые, косые, криволинейные, ломанные, кольцевые и боковые. Расход воды через водослив определяется по формулам
или
Коэффициент расхода не является величиной постоянной и зависит от типа водослива, напора, скорости подхода, наличия бокового сжатия, подтопления и других условий. Значения коэффициентов m для неподтопленных водосливов при ориентировочных расчетах рекомендуется принимать следующие: - с тонкой стенкой 0,42; - без вакуумного практического профиля 0,45; - вакуумного 0,5; - с широким порогом 0,32-0,35. Коэффициент расхода через незатопленный водослив с тонкой стенкой без бокового сжатия струи (рис. 62а) определяется по формуле
Рис. 62 Водослив с тонкой стенкой
При условии
где Н - напор, м;
Водослив становится затопленным при выполнении следующих условий: - уровень нижнего бьефа должен быть расположен выше порога водослива; - сопряжение падающей с водослива струи с нижним бьефом должно происходить при затопленном прыжке. Для затопленного водослива с тонкой стенкой расход определяется по формуле
где
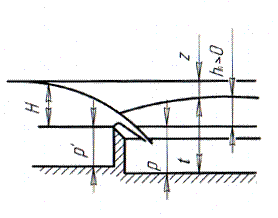
Водослив с широким порогом (рис. 63) является наиболее распространенным типом водосбросного сооружения и представляет собой порог с горизонтальной сливной плоскостью длиной
Рис. 63. Водослив с широким порогом
Расход воды через водослив с широким порогом определяется по формуле
Коэффициент расхода m рекомендуется определять согласно исследованиям проф. А.Р. Березинского. Водосливы практических профилей бывают безвакуумные и вакуумные, а по своему очертанию – криволинейные, прямоугольные, трапецеидальные и полигональные. При проектировании ответственных сооружений коэффициент расхода водослива определяется на основании лабораторных гидравлических исследований.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

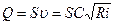 ,
, 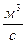 (188)
(188) ,
, 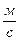 (189)
(189)
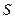

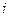
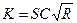 (190)
(190)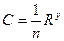 (191)
(191)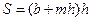 , м 2 (192)
, м 2 (192) (193)
(193)
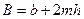 , м (194)
, м (194)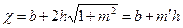 , м (195)
, м (195) ; (196)
; (196) , м 2 (198)
, м 2 (198) , м (199)
, м (199)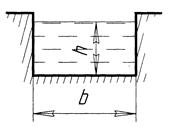
 , м (200)
, м (200) , м 2 (201)
, м 2 (201)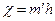 , м (202)
, м (202) , м (203)
, м (203)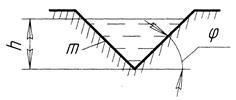

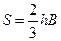 , м 2 (204)
, м 2 (204)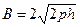 , м (205)
, м (205) - параметр параболы.
- параметр параболы. ,
, 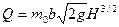 ,
, 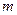
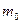
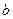
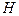
 ;
;
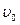
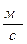 .
.
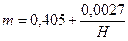 ; (208)
; (208)
 и
и 
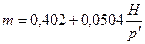 (209)
(209)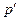 - высота стенки со стороны верхнего бьефа, м.
- высота стенки со стороны верхнего бьефа, м.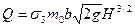 ,
,  - коэффициент затопления.
- коэффициент затопления.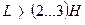 и с произвольно очерченными верховой и низовой гранями.
и с произвольно очерченными верховой и низовой гранями.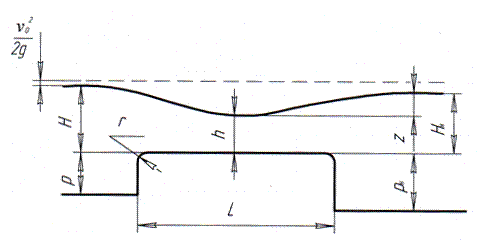
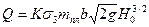 ,
,