
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление жидкости на наклонную поверхностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как и любой вектор, сила гидростатического давления, действующая на смоченную часть поверхности S плоской стенки произвольной формы, характеризуется величиной (модулем), направлением и точкой приложения. Предположим, что жидкость действует на наклоненную под углом Определим величину силы
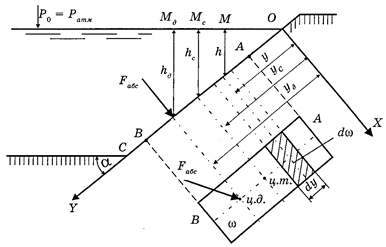
Рис. 14. К вопросу давления жидкости на плоские стенки
На рис. 14 линия АВ – проекция плоской фигуры площадью
Интеграл
Подставляем значения в выражение силы Р, имеем:
Таким образом, величина абсолютного гидростатического давления равна произведению площади смоченной части плоской стенки на гидростатическое давление в центре тяжести. Центр давления – точка приложения равнодействующей избыточного гидростатического давления, необходима для определения размеров щитов, затворов и других сооружений. Для определения координат
Момент равнодействующей
Сумму моментов
В выражении (31)
Из условия (29) видно, что
тогда координата центра давления
Из рисунка 14: заменим выражение
Известно также, что
где Подставив (34) и (35) в (33), получим
или
где Глубина погружения центра давления может быть определена по формуле:
Вектор силы давления жидкости на Криволинейную стенку В отличие от плоской стенки гидростатическое давление в разных точках криволинейной стенки различается не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующую на криволинейную стенку, непосредственно определить нельзя: ее находят через составляющие этого вектора.
 
Рис. 15. К определению силы давления на криволинейную стенку
Рассмотрим криволинейную поверхность АВ, подверженную действию избыточного гидростатического давления (жидкость справа) (рис. 15). Выделим площадку
Разложим - горизонтальная составляющая силы
- вертикальная составляющая силы
где
Рассмотрим каждую в отдельную составляющую силы избыточного давления, действующего на криволинейную поверхность АВ. Элементарная горизонтальная составляющая силы избыточного давления равна
В то же время
Следовательно
Из рис. 15 видно, что
где Откуда
Горизонтальная составляющая силы избыточного давления после интегрирования равна
где
т.е. статический момент инерции равен произведению Откуда находим
Элементарная вертикальная составляющая силы избыточного гидростатического давления равна:
Величина
Заметим, что Произведение
Отсюда вертикальная составляющая силы избыточного гидростатического давления будет равна
После интегрирования находим:
где Объем Тело давления – это объем, ограниченный криволинейной поверхностью АВ, ее проекцией на уровень свободной поверхности АВ и вертикальными плоскостями проецирования. Полная сила гидростатического давления определяется из выражения
Направление полной силы
Полная сила избыточного гидростатического давления приложена в центре давления. Вектор полной силы давления Таким образом, центр давления для криволинейных поверхностей находится графоаналитическим путем. Если криволинейная поверхность цилиндрическая, то сила
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

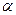 к горизонту стенку ОС (рис. 14).
к горизонту стенку ОС (рис. 14).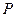 абсолютного давления на плоскую фигуру АВ, расположенную на стенке ОС (рис. 14) /4/.
абсолютного давления на плоскую фигуру АВ, расположенную на стенке ОС (рис. 14) /4/.
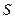 на ось
на ось 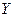 . Для определения силы гидростатического давления выделим на смоченной поверхности элементарную площадку
. Для определения силы гидростатического давления выделим на смоченной поверхности элементарную площадку 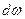 , на которую действует сила
, на которую действует сила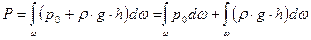
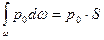
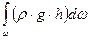
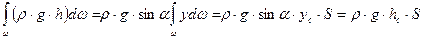
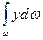 здесь выражает статический момент площади фигуры АВ относительно оси Х, т.е.
здесь выражает статический момент площади фигуры АВ относительно оси Х, т.е.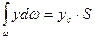
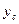
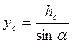 ;
;
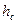
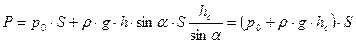 (28)
(28) ,
,  центра давления гидростатической силы воспользуемся теоремой Вариньона: если произвольная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов всех сил этой системы относительно той же оси, или
центра давления гидростатической силы воспользуемся теоремой Вариньона: если произвольная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов всех сил этой системы относительно той же оси, или (29)
(29)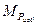

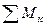
 .
.
 относительно оси Х
относительно оси Х (30)
(30)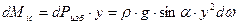 (31)
(31)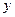
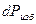 относительно оси Х.
относительно оси Х.
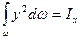 - момент инерции плоской фигуры АВ относительно оси Х, следовательно
- момент инерции плоской фигуры АВ относительно оси Х, следовательно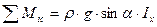 (32)
(32)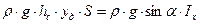 ,
, (33)
(33)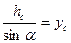 (34)
(34)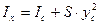 , (35)
, (35) ;
; , (36)
, (36)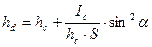 (37)
(37) . На площадку
. На площадку 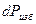 :
: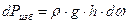 , Н (38)
, Н (38) на составляющие:
на составляющие: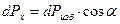 , Н (39)
, Н (39)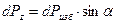 , Н. (40)
, Н. (40) .
.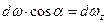 ,
,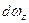 - площадь проекции элементарной площадки
- площадь проекции элементарной площадки 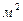 .
.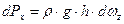 .
.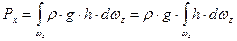 (41)
(41) - статический момент инерции всей площади проекции
- статический момент инерции всей площади проекции 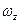 относительно свободной поверхности жидкости,
относительно свободной поверхности жидкости, 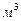 ;
;
 площади вертикальной проекции
площади вертикальной проекции  (42)
(42)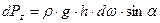
 является площадью проекции
является площадью проекции 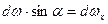 . Следовательно
. Следовательно .
.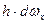 представляет собой бесконечно малый объем
представляет собой бесконечно малый объем 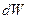 бесконечно малой призмы, отмеченной на рис. 15 штриховкой.
бесконечно малой призмы, отмеченной на рис. 15 штриховкой.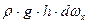 является силой тяжести в этом бесконечно малом объеме
является силой тяжести в этом бесконечно малом объеме  .
. .
.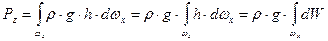 ;
;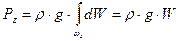 ;
;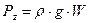 . (44)
. (44) - тело давления,
- тело давления, 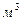 .
.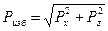 (45)
(45)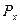
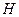 ;
;

 определяется углом
определяется углом 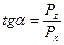 .
.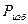 должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих, т.е.
должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих, т.е. 


