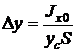Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидростатическое давление: атмосферное, избыточное, вакууметрическое, абсолютное.Содержание книги
Поиск на нашем сайте
Давление в жидкости измеряется приборами: ¾ пьезометрами, ¾ манометрами, ¾ вакуумметрами. Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1 кгс/см2= 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению pман прибавить атмосферное давление pатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной pатм= = 101325 » 100000 Па. Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 2), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению где hp — пьезометрический напор (высота), м. Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов. В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp. Манометрычаще всего применяются механические, реже — жидкостные. Все манометры измеряют не полное давление, а избыточное Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа (см. на с. 54). Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере (см. с. 8). Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере. Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости — это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину pв, которая измеряется вакуумметром. Вакуумметрическое давление pв, показываемое прибором, связано с полным и атмосферным так:
Величина вакуума pв не может быть быть больше 1 ат, то есть предельное значение pв» 100000 Па, так как полное давление не может быть меньше абсолютного нуля. Приведём примеры снятия показаний с приборов: — пьезометр, показывающий hp= 160 см вод. ст., соответствует в единицах СИ давлениям pизб= 16000 Па и p= 100000+16000=116000 Па; — манометр с показаниями pман = 2,5 кгс/см2 соответствует водяному столбу hp= 25 м и полному давлению в СИ p = 0,35 МПа; — вакуумметр, показывающий pв= 0,04 МПа, соответствует полному давлению p= 100000-40000=60000 Па, что составляет 60 % от атмосферного.
6.Основное уравнение гидростатики (вывод). Закон Паскаля. Гидростатический парадокс. Героновы фонтаны, устройство, принцип действия. Основное уравнение гидростатики гласит, что полное давление в жидкости p равно сумме внешнего давления на жидкость po и давления веса столба жидкости pж, то есть: В частном случае для открытых резервуаров, сообщающихся с атмосферой (рис. 2), внешнее давление на жидкость равно атмосферному давлению p o = pатм = 101325 Па
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости
Гидростатический парадокс - свойство жидкостей, заключающееся в том, что сила тяжести жидкости, налитой в сосуд, может отличаться от силы, с которой эта жидкость действует на дно сосуда. Героновы фонтаны. Знаменитый ученый древности Герон Александрийский придумал оригинальную конструкцию фонтана, которая находит применение и в наши дни. Главное чудо этого фонтана заключалось в том, что вода из фонтана била сама, без использования, какого либо внешнего источника воды. Принцип работы фонтана хорошо виден на рисунке. Схема устройства фонтана Герона Геронов фонтан состоит из открытой чаши и двух герметичных сосудов расположенных под чашей. Из верхней чаши в нижнюю емкость, идет полностью герметичная трубка. Если налить в верхнюю чашу воды, то вода по трубке начинает стекать в нижнюю емкость, вытесняя оттуда воздух. Поскольку сама нижняя емкость полностью герметична, то воздух выталкиваемый водой, по герметичной трубке, передает воздушное давление в среднюю чашу. Давление воздуха в средней емкости начинает выталкивать воду, и фонтан начинает работать. Если для начала работы, в верхнюю чашу требовалось налить воды, то для дальнейшей работы фонтана, уже использовалась вода попадавшая в чашу из средней емкости. Как видно устройство фонтана очень простое, но это только на первый взгляд. Подъем воды в верхнюю чашу осуществляется за счет напора воды высотой H1, при этом воду фонтан поднимает на гораздо большую высоту H2, что на первый взгляд кажется невозможным. Ведь на это должно потребоваться гораздо большее давление. Фонтан не должен работать. Но знание древних Греков оказалось столь высоко, что они догадались передавать давление воды из нижнего сосуда, в средний сосуд, не водой, а воздухом. Поскольку вес воздуха значительно ниже веса воды, потери давления на этом участке получаются очень незначительными, и фонтан бьет из чаши на высоту H3. Высота струи фонтана H3, без учета потерь давления в трубках, будет равна высоте напора воды H1. Таким образом, чтобы вода фонтана била максимально высоко, необходимо как можно выше сделать конструкцию фонтана, тем самым увеличив расстояние H1. Кроме того, нужно как можно выше поднять средний сосуд. Что касается закона физики о сохранении энергии, то он полностью соблюдается. Вода из среднего сосуда, под действием гравитации стекает в нижний сосуд. То, что она проделывает этот путь через верхнюю чашу, и при этом бьет там фонтаном, ни сколько не противоречит закону о сохранении энергии. Когда вся вода из среднего сосуда, перетечет в нижний, и фонтан перестанет работать.
7. Приборы, применяемые для измерения давления (атмосферного, избыточного, вакууметрического). Устройство, принцип действия. Класс точности приборов. Давление в жидкости измеряется приборами: ¾ пьезометрами, ¾ манометрами, ¾ вакуумметрами. Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1 кгс/см2= 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению pман прибавить атмосферное давление pатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной pатм= = 101325 » 100000 Па. Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 2), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению , где hp — пьезометрический напор (высота), м. Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов. В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp. Манометрычаще всего применяются механические, реже — жидкостные. Все манометры измеряют не полное давление, а избыточное Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере. Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости — это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину pв, которая измеряется вакуумметром. Вакуумметрическое давление pв, показываемое прибором, связано с полным и атмосферным так: Величина вакуума pв не может быть быть больше 1 ат, то есть предельное значение pв» 100000 Па, так как полное давление не может быть меньше абсолютного нуля. Приведём примеры снятия показаний с приборов: — пьезометр, показывающий hp= 160 см вод. ст., соответствует в единицах СИ давлениям pизб= 16000 Па и p= 100000+16000=116000 Па; — манометр с показаниями pман = 2,5 кгс/см2 соответствует водяному столбу hp= 25 м и полному давлению в СИ p = 0,35 МПа; — вакуумметр, показывающий pв= 0,04 МПа, соответствует полному давлению p= 100000-40000=60000 Па, что составляет 60 % от атмосферного.
8.Дифференциальные уравнения покоящейся идеальной жидкости (Уравнения Л.Эйлера). Вывод уравнений, пример применения уравнений для решения практических задач.
Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что
В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:
Выражая полную производную через конвективную производную и частную производную:
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
— оператор набла для трёхмерного пространства.
Определение силы гидростатического давления на плоскую стенку, расположенную под углом к горизонту. Центр давления. Положение центра давления в случае прямоугольной площадки, верхняя кромка которой лежит на уровне свободной поверхности. Используем основное уравнение гидростатики (2.1) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.6).
Рис. 2.6 Вычислим полную силу P давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S. Ось 0x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно этой линии в плоскости стенки. Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS: Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси 0x и равен произведению этой площади на координату ее центра тяжести (точка С), т. е. т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади. Найдем положение центра давления. Так как внешнее давление p0 передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, согласно которому момент равнодействующей силы давления относительно оси 0x равен сумме моментов составляющих сил, т. е. Выражая Pизб и dPизб через yc и y и определяя yD, получим В частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится из геометрических соображений. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.7), центр тяжести которого отстоит от основания на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на том же расстоянии от основания.
Рис. 2.7 В машиностроении часто приходится сталкиваться с действием силы давления на плоские стенки, например на стенки поршней или цилиндров гидравлических машин. Обычно p0 при этом бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки.
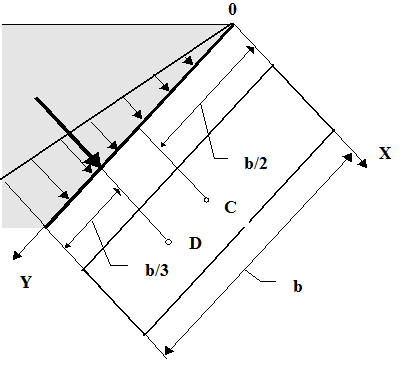
Центр давления точка, в которой линия действия равнодействующей приложенных к покоящемуся или движущемуся телу сил давления окружающей среды (жидкости, газа), пересекается с некоторой проведённой в теле плоскостью. Например, для крыла самолёта (рис.) Ц. д. определяют как точку пересечения линии действия аэродинамической силы с плоскостью хорд крыла; для тела вращения (корпус ракеты, дирижабля, мины и др.) — как точку пересечения аэродинамической силы с плоскостью симметрии тела, перпендикулярной к плоскости, проходящей через ось симметрии и вектор скорости центра тяжести тела. Положение Ц. д. зависит от формы тела, а у движущегося тела может ещё зависеть от направления движения и от свойств окружающей среды (её сжимаемости). Так, у крыла самолёта, в зависимости от форм его профиля, положение Ц. д. может изменяться с изменением угла атаки α, а может оставаться неизменным («профиль с постоянным Ц. д.»); в последнем случае хцд ≈ 0,25 b (рис.). При движении со сверхзвуковой скоростью Ц. д. значительно смещается к хвосту из-за влияния сжимаемости воздуха. Изменение положения Ц. д. у движущихся объектов (самолёт, ракета, мина и др.) существенно влияет на устойчивость их движения. Чтобы их движение было устойчивым при случайном изменении угла атаки а, Ц. д. должен сместиться так, чтобы момент аэродинамической силы относительно центра тяжести вызвал возвращение объекта в исходное положение (например, при увеличении а Ц. д. должен сместиться к хвосту). Для обеспечения устойчивости объект часто снабжают соответствующим хвостовым оперением. Лит.: Лойцянский Л. Г., Механика жидкости и газа, 3 изд., М., 1970; Голубев В. В., Лекции по теории крыла, М. — Л., 1949.
Положение центра давления потока на крыло: b — хорда; α — угол атаки; ν — вектор скорости потока; хдц — расстояние центра давления от носика тела.
10. Определение силы гидростатического давления на криволинейную поверхность. Эксцентриситет. Объем тела давления.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 5489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.231 (0.009 с.) |

 ,
, .
. .
. Если давление Р отсчитывают от абсолютного нуля, то его называют абсолютным давлением Рабс. Если давление отсчитывают от атмосферного, то оно называется избыточным (манометрическим) Ризб. Оно измеряется манометром. Атмосферное давление постоянно Ратм = 103 кПа (рис.1.5). Вакуумметрическое давление Рвак - недостаток давления до атмосферного.
Если давление Р отсчитывают от абсолютного нуля, то его называют абсолютным давлением Рабс. Если давление отсчитывают от атмосферного, то оно называется избыточным (манометрическим) Ризб. Оно измеряется манометром. Атмосферное давление постоянно Ратм = 103 кПа (рис.1.5). Вакуумметрическое давление Рвак - недостаток давления до атмосферного. , где h — высота столба жидкости над точкой (глубина её погружения), в которой определяется давление. Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной.
, где h — высота столба жидкости над точкой (глубина её погружения), в которой определяется давление. Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной. 1 ат. Тогда основное уравнение гидростатики принимает вид
1 ат. Тогда основное уравнение гидростатики принимает вид .
. .
. Закон Паскаля звучит так: внешнее давление, приложенное к жидкости, находящейся в замкнутом резервуаре, передаётся внутри жидкости во все её точки без изменения. На этом законе основано действие многих гидравлических устройств: гидродомкратов, гидропрессов, гидропривода машин, тормозных систем автомобилей.
Закон Паскаля звучит так: внешнее давление, приложенное к жидкости, находящейся в замкнутом резервуаре, передаётся внутри жидкости во все её точки без изменения. На этом законе основано действие многих гидравлических устройств: гидродомкратов, гидропрессов, гидропривода машин, тормозных систем автомобилей.
 ,
, , где
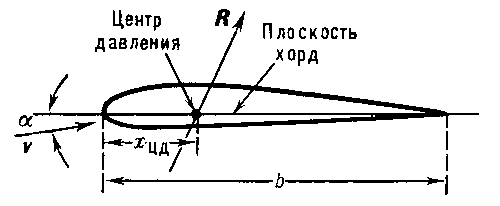
, где 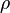 — плотность жидкости в данной точке, получим:
— плотность жидкости в данной точке, получим:



 — плотность жидкости,
— плотность жидкости, — давление в жидкости,
— давление в жидкости, — вектор скорости жидкости,
— вектор скорости жидкости, — вектор напряжённости силового поля,
— вектор напряжённости силового поля,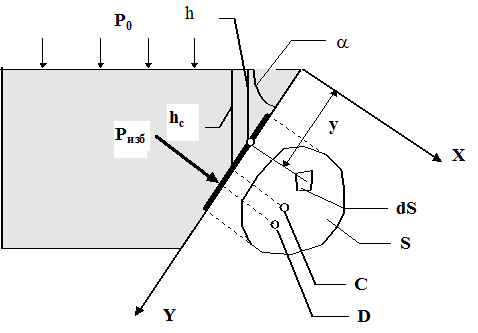
 ,
,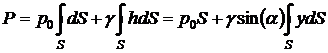 ,
,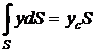

 (2.6)
(2.6)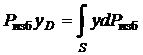

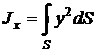 - момент инерции площади S относительно оси 0x.
- момент инерции площади S относительно оси 0x. 
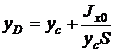 (2.7)
(2.7)