
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие «жидкость». Капельная, реальная, идеальная, упругая жидкость. Силы, действующие в жидкости.Содержание книги
Поиск на нашем сайте Понятие «жидкость». Капельная, реальная, идеальная, упругая жидкость. Силы, действующие в жидкости. Жидкость легко подвижная среда, заполняющая объем без пустот и промежутков. Жидкостью называют физическое тело, обладающее весьма большой подвижностью частиц, текучестью. Различают два вида жидкостей: капельные и газы. Капельные жидкости оказывают большое сопротивление изменению объема и трудно поддаются сжатию.(мало изменяют объем при изменении давления, легко принимают любую форму резервуара). Газы легко меняют объем при изменении давления и температуры, и имеют значительно меньшую плотность, чем капельные жидкости. В гидравлике различают жидкости реальные и идеальные. К идеальным относятся жидкости абсолютно не меняющие объем (несжимаемые), невязкие.(обладает текучестью, предложил Эйлер). Реальной жидкостью считается жидкость вязкая сжимаемая или несжимаемая.(обладает текучестью, вязкостью, сжимаемостью) В основном в гидравлике рассматриваются вязкие несжимаемые жидкости. Упругая жидкость, которую называют жидкостью Максвелла (а также телом или моделью Максвелла). Эта жидкость не подчиняется закону вязкости Ньютона и поэтому называется неньютоновской жидкостью. В гидравлике рассматривается два типа сил, действующих в жидкости: массовые и поверхностные. Массовые силы обусловлены действующим на жидкость силовым полем, они приложены к каждой частице жидкости и пропорциональны их массе, примером таких сил являются силы тяжести(G=mg), силы инерции переносного движения (Fин=ma). Поверхностные силы обусловлены взаимодействием рассматриваемого объема с окружающими его телами; силы реакции стенок сосуда; если рассматривается объем, мысленно выделенный из общей массы жидкости – это силы, действующие на него со стороны «отброшенной» жидкости, распределенные по поверхности объема и пропорциональны площади поверхности, на которую они действуют.(сила давления Р=РF/S, РF-поверхност. силы, S –площадь поверхности; сила трения τ= T/ω, T-касательная сила,ω-площадь) Рпов=2σ/r; Pпов- напряжения в жидкости,σ - коэффициент поверхностного натяжения, r - радиус сферической поверхности, которую принимает жидкость. Δh=4σ/gdρ=k/d d – диаметр капилляра, k – коэффициент пропорциональности k=4σ/gρ
Под названием жидкость подразумевается одно из агрегатных состояний вещества. Жидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления.В большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза) квантовые жидкости и жидкие кристаллы.В технической гидромеханике под жидкостью понимают физическое тело, обладающее а) в отличие от твёрдого тела текучестью и б)в отличие от газа весьма малой изменяемостью своего объёма.
Механические характеристики жидкости. Физические свойства капельной жидкости (сжимаемость, вязкость, поверхностное натяжение, температурное расширение, капиллярность, испаряемость, растворимость газов.) Плотностью -называется количество покоящейся массы данного вещества, заключенного в единице его объема. ρ=m/V (кг/м3) относительная плотность-соотношение плотности в-ва к плотности воды при -4 0 С Удельный вес – вес единицы объема жидкости γ=G/V (H/ м3), γ=ρg; G вес жидкости в объеме V Удельный объем – объем единицы массы покоящейся жидкости υ=1/ρ (м3/кг) Текучесть - это легкоподвижность частиц жидкости, обусловловленная ее неспособностью воспринимать касательные напряжения в состоянии покоя. Поэтому жидкость не может сохранять собственную форму, а принимает форму сосуда (резервуара, водоема), в котором находится. Сжимаемость - способность жидкостей уменьшать объем при увеличении давления. Характеризуется коэффициентом объемного сжатия βW, который представляет собой относительное изменение объема жидкости на единицу изменения давления: βW = - ΔV/VΔp, где V - первоначальный объем жидкости; ΔV - приращение (изменение) этого объема при увеличении давления на величину Δρ. Коэффициент объемного сжатия в системе СИ имеет размерность Па-1. Знак минус в этой формуле обусловлен тем, что положительному приращению давления ρ соответствует отрицательное приращение (т.е. уменьшение) объема жидкости. Вязкость жидкостей - свойство жидкости сопротивляться относительному движению (сдвигу) ее частиц, обусловливающее появление силы внутреннего трения между слоями жидкости, если последние имеют различные скорости движения.(св-во обратное текучести). Это свойство характеризуется коэффициентами динамической μ и кинематической ν вязкостей. μ= τ/du*dy, Где τ-сила, которая возникает на единице площади поверхности двух движущихся друг относительно друга слоев жидкости при градиенте скорости равный 1 (du -разность скоростей перемещающихся слоев воды, dy - толщина слоя). В международной системе единиц динамическая вязкость выражается в Н*с/м2 или Па*с В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости ν (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости: ν=μ/ρ, Вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает Сила поверхностного натяжения - это сила, обусловленная взаимным притяжением молекул жидкости, направленная по касательной к ее поверхности. Силы, действующие на поверхности раздела газ-жидкость, стремятся придать малому объему жидкости сферическую форму: Ep = Aвнеш = σS, Ep -потенциальной энергией, ΔAвнеш-работa внешних сил, S- площади поверхности, σ-коэффициент поверхностного натяжения(1 Н/м = 1 Дж/м2) σ= FH/2L Δρ=2σ/r (для мыльного пузыря) Δρ-избыточное давление, σ-коэф. поверхностного натяжения, r-радиус; Δρ=4σ/r (капля жидкости) Температурное расширение - способность жидкостей изменять объем при изменении температуры. Для капельных жидкостей характеризуется коэффициентом температурного расширения βT, равным относительному изменению объема при изменении температуры t на один градус при постоянном давлении: βT= ΔV/VΔt, где V- первоначальный объем; ΔV- изменение этого объема при повышении температуры на величину Δt.Коэффициент температурного расширения в системе СИ имеет размерность град-1.Коэффициент зависит для данной жидкости от температуры и давления. Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. h=2σcosθ/ρgr При полном смачивании θ = 0, cos θ = 1 h=2σ/ρgr=4σ/γd, θ-угол смачивания,ρ-плотность, γ-удельный вес, Испаряемость жидкостей. При повышении температуры жидкости и, в некоторых случаях, при снижении давления часть массы капельной жидкости постепенно переходит в газообразное состояние (пар). Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Однако, чем больше насыщенность паров при данной температуре, тем больше испаряемость жидкости. Растворение газов -способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости kр. VГ/ Vж = kр P1 / P 2 где VГ– объём растворённого газа при нормальных условиях, Vж– объём жидкости, P1 и P2– начальное и конечное давление газа. Коэффициент растворимости зависит от типа жидкости, газа и температуры.
Гидростатическое давление (ГД). Два основных свойства ГД (с доказательством). Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна. P ср =ΔP/ΔS
Рассмотрим силу гидростатического давления Р, приложенную в точке С под углом к поверхности А—В объема жидкости, находящегося в покое. Тогда эту силу можно разложить на две составляющие: нормальную Рп и касательную Рt к поверхности А—В. Касательная составляющая—это равнодействующая сил трения, приходящихся на выделенную поверхность вокруг точки С. Но так как жидкость находится в покое, то силы трения отсутствуют, т. е. Рt =0. Следовательно, сила гидростатического давления Р в точке С действует лишь в направлении силы Рп, т. е. нормально к поверхности А—В. Причем направлена она только по внутренней нормали. При предположении направления силы гидростатического давления по внешней нормали возникнут растягивающие усилия, что приведет жидкость в движение. А это противоречит условию. Таким образом, сила гидростатического давления всегда сжимающая, т. е. направлена но внутренней нормали.
Для доказательства этого свойства выделим в жидкости, находящейся в равновесии, частицу в форме треугольной призмы с основанием в виде прямоугольного треугольника А—В—С. Будем рассматривать этот объём в некоторой произвольной системе координат X,Y,Z. При этом ось у перпендикулярна плоскости. Заменим действие жидкости вне призмы на ее боковые грани гидростатическим давлением соответственно Pх, Pz, Pе. Px=px*dz*dy Pz=pz*dx*dy Pe=pe*de*dy Кроме этих сил на призму действует сила тяжести dG, равная весу призмы g*dz*dx*dy/2. Силой тяжестью можно пренебречь. Так как она будет величиной 3-го порядка малости, а силы действующие на грани призмы 2 –го порядка малости. Так как частица жидкости находится в равновесии, в покое, то сумма проекций всех сил, приложенных к ней, на любое направление равна нулю т.е. ∑x=0; px*dz*dy- pe*de*dy*sinα=0 ∑z=0; pz*dx*dy- pe*de*dy*cosα=0 Подставляя dz=de sina и dx=de cosa в предыдущие уравнения и разделив каждое уравнение dy, получим ∑x=0; px*dz - pe*dz =0 ∑z=0; pz*dx - pe*dx =0, Из выражений следует px= pz= pe Следовательно, гидростатическое давление на наклонную грань Ре одинаково по величине с гидростатическим давлением на вертикальную и горизонтальную грани. Так как угол наклона грани a взят произвольно, то можно утверждать, что гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. P = f (x, y, z )
Определение силы гидростатического давления на плоскую стенку, расположенную под углом к горизонту. Центр давления. Положение центра давления в случае прямоугольной площадки, верхняя кромка которой лежит на уровне свободной поверхности. Используем основное уравнение гидростатики (2.1) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.6).
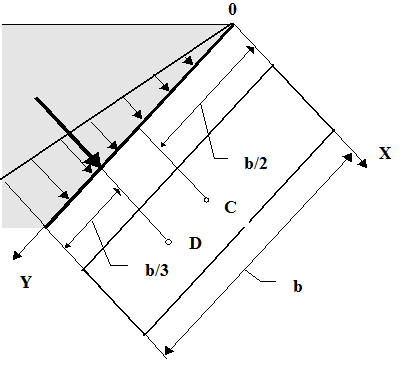
Рис. 2.6 Вычислим полную силу P давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S. Ось 0x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно этой линии в плоскости стенки. Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS: Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси 0x и равен произведению этой площади на координату ее центра тяжести (точка С), т. е. т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади. Найдем положение центра давления. Так как внешнее давление p0 передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, согласно которому момент равнодействующей силы давления относительно оси 0x равен сумме моментов составляющих сил, т. е. Выражая Pизб и dPизб через yc и y и определяя yD, получим В частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится из геометрических соображений. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.7), центр тяжести которого отстоит от основания на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на том же расстоянии от основания.
Рис. 2.7 В машиностроении часто приходится сталкиваться с действием силы давления на плоские стенки, например на стенки поршней или цилиндров гидравлических машин. Обычно p0 при этом бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки.
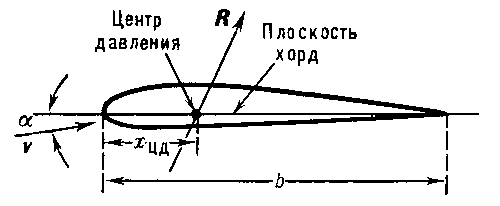
Центр давления точка, в которой линия действия равнодействующей приложенных к покоящемуся или движущемуся телу сил давления окружающей среды (жидкости, газа), пересекается с некоторой проведённой в теле плоскостью. Например, для крыла самолёта (рис.) Ц. д. определяют как точку пересечения линии действия аэродинамической силы с плоскостью хорд крыла; для тела вращения (корпус ракеты, дирижабля, мины и др.) — как точку пересечения аэродинамической силы с плоскостью симметрии тела, перпендикулярной к плоскости, проходящей через ось симметрии и вектор скорости центра тяжести тела. Положение Ц. д. зависит от формы тела, а у движущегося тела может ещё зависеть от направления движения и от свойств окружающей среды (её сжимаемости). Так, у крыла самолёта, в зависимости от форм его профиля, положение Ц. д. может изменяться с изменением угла атаки α, а может оставаться неизменным («профиль с постоянным Ц. д.»); в последнем случае хцд ≈ 0,25 b (рис.). При движении со сверхзвуковой скоростью Ц. д. значительно смещается к хвосту из-за влияния сжимаемости воздуха. Изменение положения Ц. д. у движущихся объектов (самолёт, ракета, мина и др.) существенно влияет на устойчивость их движения. Чтобы их движение было устойчивым при случайном изменении угла атаки а, Ц. д. должен сместиться так, чтобы момент аэродинамической силы относительно центра тяжести вызвал возвращение объекта в исходное положение (например, при увеличении а Ц. д. должен сместиться к хвосту). Для обеспечения устойчивости объект часто снабжают соответствующим хвостовым оперением. Лит.: Лойцянский Л. Г., Механика жидкости и газа, 3 изд., М., 1970; Голубев В. В., Лекции по теории крыла, М. — Л., 1949.
Положение центра давления потока на крыло: b — хорда; α — угол атаки; ν — вектор скорости потока; хдц — расстояние центра давления от носика тела.
10. Определение силы гидростатического давления на криволинейную поверхность. Эксцентриситет. Объем тела давления. Эксцентриситет
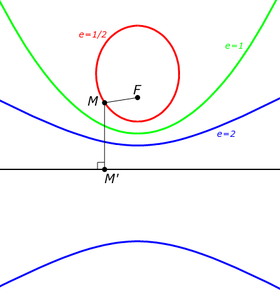
Эллипс (e =1/2), парабола (e =1) и гипербола (e =2) с фиксированными фокусом F и директрисой. (|FM| = e |MM'|) Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “ Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия. Определение Все невырожденные конические сечения, кроме окружности, можно описать следующим способом: Выберем на плоскости точку
Тело давления - объем жидкости, лежащий над криволинейной поверхностью, между вертикальными плоскостями, проходящими через крайние образующие и свободной поверхностью жидкости или ее продолжением. Тело давления – это объем, ограниченный криволинейной поверхностью, пьезометрической плоскостью и вертикальными поверхностями, проходящими через периметр криволинейной поверхности. Fверт = g*Vтд
11. Закон Архимеда. Вывод уравнения для определения Архимедовой силы. Центр водоизмещения. Условия плавания и остойчивости тела. Метацентр. Метацентрическая высота. Ватерлиния. Осадка. Запас плавучести. Закон Архимеда Закон Архимеда формулируется следующим образом[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме тела. Сила называется силой Архимеда:
где
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела. Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна. Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха. Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
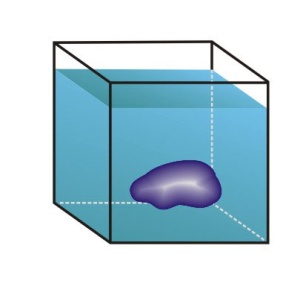
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля. Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно · g · h = p 1 а на нижнюю · g (h+a) = p 2 Сила давления равна давлению, умноженному на площадь, т.е. F 1 = p 1 · a \up122, F 2 = p 2 · a \up122, где a – ребро кубика, причем сила F 1 направлена вниз, а сила F 2 – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F 1 и F 2 и определяется их разностью, которая и является выталкивающей силой: F 2 – F 1 = · g · (h+a) a \up122 – gha · a 2 = pga 2 Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F 2 – F 1 = pga 3 равна объему тела (кубика) a 3, умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли. Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V, то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V. Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V, т.е. pgV. Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V, можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела. Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» , т.е. веса единицы объема вещества: pg; если принять, что для воды , то сплошное тело из вещества, у которого утонет, а при будет плавать на поверхности; при тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Центр величины
Схема плавающего судна. Центр величины обозначен B Центр величины (ЦВ) — в теории корабля — точка приведения сил плавучести, действующих на судно. Известен также как центр водоизмещения тела. Поскольку силы плавучести являются по природе силами давления, они действуют распределенно на всю поверхность погруженного объёма. Для расчетов удобно привести их, то есть выразить через одну равнодействующую силу, приложенную в одной точке.
Иллюстрация центра величины Иначе говоря, центр величины — это воображаемая точка приложения равнодействующей сил плавучести. Метацентр
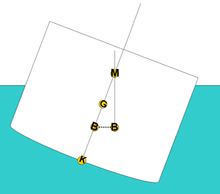
Поперечное наклонение плавающего судна. Метацентр обозначен M. Центр величины обозначен B Метацентр (от греч. μετα — через и лат. centrum — средоточие) — центр кривизны траектории, по которой перемещается центр величины в процессе наклонения судна. При малых наклонениях судна (примерно, до 10 градусов) метацентр можно считать неподвижным, при больших наклонениях метацентр начинает смещаться. Возвышение метацентра над центром тяжести судна называется метацентрической высотой. В теории корабля различают два метацентра:
На практике судно испытывает наклонения в обеих плоскостях, и если определить для этого случая метацентр, он будет лежать выше поперечного, но ниже продольного. С этой точки зрения метацентрические высоты, рассматриваемые в теории, являются предельными. Метацентрическая высота Отрезок mG — метацентрическая высота. Метацентрическая высота — критерий остойчивости судна. Представляет собой возвышение метацентра над центром тяжести плавающего тела. Чем больше этот параметр, тем выше начальная остойчивость судна. При приобретении отрицательного значения метацентрической высоты судно утрачивает способность плавать без крена. Ответить на вопрос «перевернется ли судно, имеющее отрицательную метацентрическую высоту» не представляется возможным, так как метацентрическая теория остойчивости верна лишь при наклонениях судна, не превышающих 10 градусов. Тем не менее, в Правилах классификационных обществ, осуществляющих надзор за технической эксплуатацией судов (Российский Речной Регистр, Российский Морской Регистр Судоходства и др.), запрещена эксплуатация судов, имеющих метацентрическую высоту менее 0,2 м. Характерным примером тела, имеющего нулевую метацентрическую высоту, является симметричный плавающий бочонок. При нахождении в спокойной воде такой бочонок будет совершать вращение вдоль продольной оси под воздействием любых внешних сил (например ветра).
Ватерли́ния (нидерл. waterlinie) — линия соприкосновения спокойной поверхности воды с корпусом плавающего судна. Также — в теории корабля элемент теоретического чертежа: сечение корпуса горизонтальной плоскостью. Различают следующие ватерлинии: · конструктивная ватерлиния (КВЛ) — то есть расчетная, определяемая для нормального водоизмещения. Положением этой ватерлинии определяется деление корабля на надводную и подводную части[1]; · грузовая ватерлиния — рассчитанная для заранее определенной нагрузки и условий плавания; · действующая ватерлиния — текущая, при данной нагрузке и условиях; · теоретические ватерлинии — набор сечений через равные расстояния, формирующий один из видов теоретического чертежа: план.
Изменение действующей ватерлинии в зависимости от осадки Действующая ватерлиния определяется формой судна, его средней плотностью, а также степенью волнения воды в данном бассейне. Площадь ватерлинии используется для вычисления коэффициента полноты корпуса. Форма площади ватерлинии, точнее ее момент инерции является фактором, определяющим устойчивость формы. Очевидно, в зависимости от условий нагрузки, крена и дифферента форма площади ватерлинии, а с ней и устойчивость, могут меняться. Длина по ватерлинии служит характерным линейным размером в определении числа Фруда для водоизмещающих судов, и соответственно, их теоретической скорости.
Осадка (англ. Draft) — в военном и гражданском кораблестроении — глубина погружения корабля или судна в воду. Различают следующие виды осадки. 1. Проектная или расчётная осадка, или вертикальное расстояние от верхней кромки киля до уровня главной ватерлинии, измеренное на половине длины корпуса. В технической документации обозначается как T. 2. Проектная осадка по мидельшпангоуту — расстояние от ватерлинии до наружной кромки обшивки у киля. 3. Осадка носом, измеряемая по носовой точке погружения, или у носовой марки. 4. Осадка кормой, измеряемая по кормовой точке погружения, или у кормовой марки. 5. Средняя осадка — среднее арифметическое значение носовой и кормовой осадки. Для измерения осадки на корпусе корабля наносятся марки углубления. В большинстве флотов мира марки углубления наносятся по вертикали от концевых точек прямой линии киля до главной ватерлинии с обоих бортов судна. В англо-саксонских странах (но не только в них) долей марки является фут. Для судов с большой осадкой затруднён, либо невозможен вход в мелководные районы моря, гавани, порта, а также в устья рек.
Запас плавучести Под плавучестью корабля понимают его способность оставаться на плаву при заданной нагрузке. Эта способность характеризуется запасом плавучести, который выражается как процент объёма водонепроницаемых отсеков выше ватерлинии к общему водонепроницаемому объёму. Любое нарушение непроницаемости ведёт к снижению запаса плавучести. Для корабля (судна), у которого корпус водонепроницаем по главную палубу: W = Vн / Vo * 100, где Vн — объём подпалубных помещений над ватерлинией, Vo — весь объём подпалубных помещений.
Виды движения жидкости (установившееся, неустановившееся, равномерное, неравномерное, напорное, безнапорное). Элементы потока жидкости (линия тока, поверхность тока, трубка тока, элементарная струйка, площадь живого сечения). Понятие расхода жидкости. Определение скорости осредненной по живому сечению.
Неустановившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.:
Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде пост
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 4980; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

 Первое свойство. Гидростатическое давление направлено всегда по внутренней нормали к поверхности, на которую оно действует.
Первое свойство. Гидростатическое давление направлено всегда по внутренней нормали к поверхности, на которую оно действует. Второе свойство состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление.
Второе свойство состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление.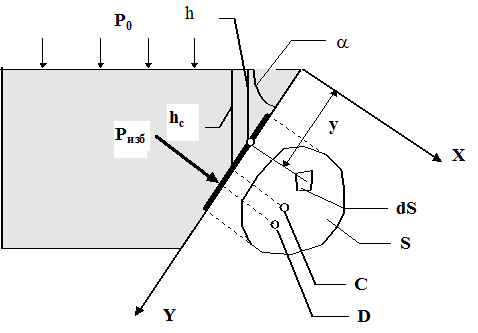
 ,
,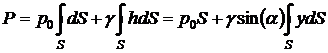 ,
,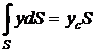

 (2.6)
(2.6)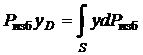

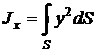 - момент инерции площади S относительно оси 0x.
- момент инерции площади S относительно оси 0x. 
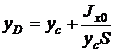 (2.7)
(2.7)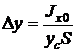
 ” или “
” или “  ”.
”.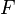 и прямую
и прямую 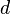 и зададим вещественное число
и зададим вещественное число 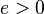 . Тогда геометрическое место точек
. Тогда геометрическое место точек  , для которых отношение расстояний до точки
, для которых отношение расстояний до точки 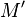 есть проекция
есть проекция 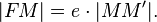
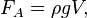
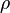 — плотность жидкости (газа),
— плотность жидкости (газа),  — ускорение свободного падения, а
— ускорение свободного падения, а 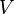 — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
— объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.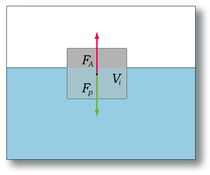
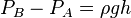


 центр водоизмещения — Центр объема жидкости, вытесненной плавающим телом в связанной с ним системе отсчета
центр водоизмещения — Центр объема жидкости, вытесненной плавающим телом в связанной с ним системе отсчета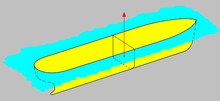
 при наклонении судна в поперечной плоскости (крен), метацентр является поперечным, или малым.
при наклонении судна в поперечной плоскости (крен), метацентр является поперечным, или малым. 
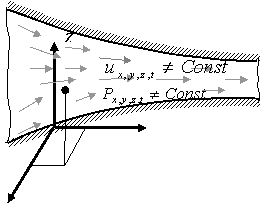 Течение жидкости вообще может быть неустановившимся (нестационарным) или установившимся (стационарным).
Течение жидкости вообще может быть неустановившимся (нестационарным) или установившимся (стационарным).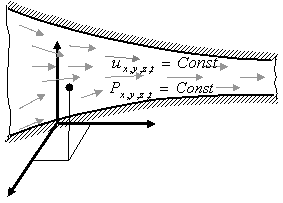
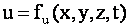 и
и 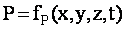 .
.


