
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Два режима движения жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гидравлика Часть II Утверждено редакционно-издательским советом университета в качестве учебного пособия
Нижний Новгород - 2005
ББК 30.123 А 23
Агеева В.В. Гидравлика. Часть II: Учебное пособие. – Н.Новгород: Нижегород. гос. архит.-строит. ун-т, 2005. – 81 с. ISBN 5-87941-342-х
Учебное пособие предназначено для студентов специальности «Промышленное и гражданское строительство» 270102 и включает разделы гидродинамики, предусмотренные учебной программой курса. .
ББК 30.123
ISBN 5-87941-342-х
© Агеева В.В., 2005, © ННГАСУ, 2005
ОСНОВЫ ГИДРОДИНАМИКИ
Гидродинамика (точнее, техническая гидродинамика) изучает законы движения жидкости, а также взаимодействие между жидкостью и твердыми телами при их относительном движении. Гидродинамика позволяет использовать эти законы при решении задач в области водоснабжения, канализации, газоснабжения, вентиляции, гидротехники и т.д. [6]. Теория технической гидродинамики, изложенная в данном пособии, строится для струйной модели жидкости и основывается на 3-х основных уравнениях, носящих общий характер: - уравнение несжимаемости и неразрывности движущейся жидкости (уравнение баланса расхода жидкости); - уравнение баланса удельной энергии потока (уравнение Бернулли); - гидравлическое уравнение количества движения.
1.1. Основные понятия и определения. Гидравлические элементы потока
Рис. 1. Схема траектории
Рис. 2. Линия тока
Поток – совокупность элементарных струек. На рис. 3: abcd – поток; kl – элементарная струйка; mn – линия тока. Живое сечение потока ω, м2 – сечение, проведенное перпендикулярно средним скоростям или линиям тока.

Рис. 3. Поток
Рис. 4. Гидравлические элементы потока
Рис. 5. Гидродинамическое давление По теории Прандтля, в действительном потоке местная скорость на оси потока (в центре тяжести потока) имеет максимальное значение
Рис. 6. Эпюра скоростей движения жидкости в трубе Расход жидкости – объем жидкости, проходящий через живое сечение за единицу времени
Уравнение Бернулли в случае установившегося движения Уравнение Бернулли является одним из основных уравнений гидродинамики. Оно устанавливает зависимость между скоростями и давлениями в различных сечениях элементарной струйки (потока). ИСТЕЧЕНИЕ ИЗ ОТВЕРСТИЙ, ЧЕРЕЗ НАСАДКИ И ВОДОСЛИВЫ Основное уравнение гидравлики – уравнение Бернулли – было получено в результате решения задачи по истечению жидкости из отверстия. Эта задача сводится к определению скорости истекания и расхода вытекающей жидкости. Опорожнение резервуара
Рассмотрим заполненный жидкостью резервуар (рис. 26):
Рис. 26. Опорожнение сосуда через отверстие в его дне:
Если за время опорожнения резервуара притока жидкости не происходит, то время на опорожнение можно рассчитать:
Принимая в формуле (57) Н2 =0, время полного опорожнения
Если выражение (58) умножить на
Таким образом:
где V – объем резервуара; Q – расход жидкости при начальном напоре Н1. Выражение (60) показывает, что время полного опорожнения резервуара при переменном напоре в 2 раза больше времени, потребного для вытекания из резервуара того же количества жидкости при постоянном напоре, равном начальному напору Н1.
Классификация водосливов
По профилю различают водосливы с тонкой стенкой (рис. 36, а), с широким порогом (рис. 36, б) и практического профиля (рис. 36, в). а) δ ≤ 0,5 Н

б) 2 Н ≤ δ ≤ 8 Н в) 0,5 Н < δ < 2 Н
Рис. 36. Водосливы различного профиля: 1 – гребень плотины; 2 – верхний бьеф (ВБ – область потока перед водосливом); 3 – нижний бьеф (НБ – область потока за водосливом); Н – геометрический напор, измеряющийся не ближе чем 3 Н от водосливной стенки; Н0 – полный напор с учетом скорости подхода υ0; δ – толщина стенки; РВ, РН – высоты стенки водослива соответственно в ВБ и НБ; z – геометрический перепад на водосливе; В – ширина водосливного фронта; hНБ – глубина в НБ По форме водосливного отверстия различают водосливы, рис. 37: а) прямоугольные; б) треугольные; в) трапецеидальные; г) круговые; д) параболические; е) с наклонным гребнем и т.д.
Рис. 37. Различные формы водосливного отверстия По очертанию гребня в плане. Здесь различают: 1) водосливы с прямолинейным в плане гребнем (рис. 38): а) прямые (лобовые); б) косые; в) боковые.
а) б) в)
Рис. 38
2) водосливы с непрямолинейным в плане гребнем (рис. 39): а) полигональные (ломаные); б) криволинейные; в) замкнутые (например, кольцевые).
а) б) в)
Рис.39 По типу сопряжения струи с нижним бьефом. Эта классификация является весьма важной. Здесь различают незатопленные (их ещё называют неподтопленные) водосливы, когда Q и Н не зависят от глубины воды в нижнем бьефе hНБ (рис. 40, а); и затопленные (подтопленные) водосливы, когда Q и (или) Н зависят от глубины воды в нижнем бьефе hНБ (рис. 40, б): а) незатопленный водослив с отогнанным прыжком;
б) затопленный водослив с тонкой стенкой.
Рис. 40
По условиям бокового сжатия потока (относится только к случаю прямоугольных водосливов) различают водосливы без бокового сжатия (когда ширина русла равна ширине водослива) и водосливы с боковым сжатием (ширина русла больше ширины водослива).
Расчет водослива
Существует формула для большого прямоугольного отверстия (56):
Понизим уровень воды (рис. 41) до Н1 (Н1 и Н2 – соответственно расстояние от уровня воды в резервуаре до верхней и нижней кромок отверстия). Тогда выражение (56) примет вид:
Обозначим произведение двух постоянных буквой т: Явление истечения из отверстия перешло в явление истечения через водослив
где т – коэффициент водослива, и его не следует смешивать с коэффициентом расхода, относящимся к случаю истечения через трубы, отверстия, насадки. Коэффициент т различен для разных типов водосливов и для различных условий их работы (см. гидравлические справочники [6]). Формула (76) является основной расчетной формулой для прямоугольного водослива, и получил ее Пьер Дюбуа.
Рис. 41
Мерные водосливы Здесь рассматриваются неподтопленные водосливы. 1. В 1861 г. английский профессор Джемс Томсон предложил для измерения расходов воды треугольный водослив (рис. 42, а). Для водослива с углом при основании 90° он нашел формулу:
Опыты, проведенные в 1916 г. Генри Кингом в Мичиганском университете (США), позволили ему несколько уточнить формулу (87):
В настоящее время находят применение обе формулы. В гидравлических справочниках [6] приводятся графики и таблицы с величинами расхода треугольного водослива, вычисленными по формулам (87), (88). 2. Итальянским ученым Чиполетти предложен трапецеидальный водослив с вертикальной тонкой стенкой (рис. 42, б). По опытам, выполненным им в 1887 г. в Миланском университете, дана формула в метровой размерности (ctg Θ =1/4; b= 4 Н)
Рис. 42. Мерные водосливы Длинные трубопроводы Простой трубопровод Напомним, что в случае длинных трубопроводов местными потерями напора пренебрегаем; кроме того, считаем, что линия Е-Е совпадает с линией Р-Р. Простой трубопровод не имеет ответвлений. Основные задачи при расчете простого длинного трубопровода. Пусть имеются два резервуара: питающий А и расходующий В с установившейся разностью уровней Н, соединенные между собой трубопроводом длиной l и постоянным диаметром d. В других случаях роль верхнего резервуара может выполнять насос, установленный в начале трубопровода и создающий там давление р=ρghA. Нижний резервуар тоже может отсутствовать, и жидкость будет вытекать в атмосферу через отверстие в конце трубопровода. Пусть резервуары открыты и давление на свободной поверхности жидкости равно атмосферному. Составим уравнение Бернулли для сечений, показанных на рис. 43.
Рис. 43. Простой длинный трубопровод одного диаметра
Для сечения 1-1: Для сечения 2-2: z1 =0, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости. υ2= 0,
Таким образом, При расчете простого трубопровода длина l его обычно известна, так же как материал и конфигурация труб. Неизвестной может быть одна из трех величин – H, Q или d. В соответствии с опытом могут быть рассмотрены три основных типа задач: 1-й тип: Дано: Q, d, l. Определить: H. Решаем по уравнению (**), предварительно находим величину K по диаметру d [6]. 2-й тип: Дано: d, l, H. Определить: Q. Решаем по уравнению (**), предварительно находим K по диаметру d [6]. 3-й тип: Дано: l, Q, H. Определить: d. По заданным l, Q, H по уравнению (**) определяем K, затем по таблицам [6] находим диаметр d. Истечение под уровень. Пьезометрическая линия Р-Р (она же Е-Е) должна иметь вид, показанный на рис. 44. Чем больше скорость в трубе, тем больше потеря напора, а следовательно, и величина I. Поэтому при d1 < d 2 пьезометрический уклон I1 должен быть больше пьезометрического уклона I2. Разность уровней жидкости в сосудах z при истечении под уровень равна потере напора:
где hl1, hl2, hl3 – потери напора по длине соответственно для 1, 2, 3-й труб, показанных на рис. 44.
Рис. 44. Простой длинный трубопровод переменного диаметра
В случае длинных труб hl определяется по формуле (99). Учитывая это, перепишем (102)
где К1, К2, К3 – модули расходов для 1, 2, 3-й труб; l1, l2, l3 – длины этих труб; Q – расход, одинаковый для всех трех труб. Вынося Q за скобки, вместо (103) получаем:
Тогда расход:
Короткие трубопроводы
Как уже отмечалось, в коротких трубопроводах потери на местных сопротивлениях соизмеримы с линейными, следовательно при расчете учитываются и hj, и hl. Расчет самотечных труб. Рассматриваем установившееся движение; разность уровней в водоемах, соединяемых трубопроводом, постоянна. Расчет сводится к определению величины расхода, используя уравнение Бернулли.
Рис. 47. Самотечная линия Пример. Вода из реки поступает в колодец по трубопроводу (затем отбирается из него насосом). Решение. Для выбранных сечений, рис. 47, будем иметь следующее:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости. υ2= 0,
H=hf, (113) то есть в самотечных линиях напор зависит от количества линейных и местных сопротивлений. Для условий нашей задачи выражение (113) примет вид
где υ – средняя скорость воды в трубе. Ее можно выразить из (114)
Обозначим первое подкоренное выражение в (115) буквой μ, этот коэффициент называется коэффициентом расхода системы, причем:
Тогда:
В самотечных линиях отложение взвешенных частиц ведет к засорению трубопровода и колодца, и поэтому трубы укладывают с уклоном в сторону водоема для промывки. Всасывающая линия насоса. Расчет обычно сводится к определению высоты установки насоса hнас. Всасывающая линия (труба) характеризуется наличием вакуума. Наибольшая величина вакуума будет непосредственно у насоса, перед его рабочим колесом (в сечении 2-2), рис. 48. И высоту установки насоса, и вакуум его можно найти, соединяя уравнением Бернулли сечение 1-1, намеченное по поверхности жидкости в колодце, и сечение 2-2, проведенное по вертикальной оси насоса. Запишем уравнение:
Рис. 48. Всасывающая труба насоса
Для сечения 1-1: Для сечения 2-2: z1 =0, z2 = hнас, p1=pатм, p2 –давление в трубе перед насосом, υ1= 0 ввиду малости, υ2 – скорость в трубе,
Получаем:
Выражение (122) показывает превышение атмосферного давления над давлением p2 в парубке у входа в насос и является вакуумом насоса или вакуумметрической высотой всасывания. Перепишем (121) с учетом (122)
Если Нвак оказывается большим, то при этом возникает кавитация, которая обусловливает снижение коэффициента полезного действия насоса. Различные типы насосов допускают различную величину вакуума. Обычно вакуум перед рабочим колесом насоса должен удовлетворять условию Нвак ≤4,0÷6,5 м вод.ст. Пример. Насос забирает воду из водоема (tводы =20°С) в количестве Q= 50 л/с. Определить максимальную высоту расположения горизонтального вала насоса над свободной поверхностью воды hнас, если давление перед насосом р2= 0,3·105 Па. На всасывающей чугунной трубе, бывшей в употреблении, диаметром d =250 мм и длиной l= 50 м имеется заборная сетка Решение. Расход Q= 50 л/с=5·10-2 м3/с. Выпишем сведения из гидравлического справочника [6]: 1. Коэффициент кинематической вязкости для воды при температуре tводы =20°С равен ν =0,0101 см2/с=0,1·10-6 м2/с; 2. Для чугунной бывшей в употреблении трубы коэффициент эквивалентной шероховатости КЭ =1 мм; 3. Коэффициенты местных сопротивлений 4. Формула Альтшуля: Высоту постановки насоса над уровнем воды можно определить по формуле (121). Предварительно вычислим скорость воды в трубе по формуле, вытекающей из уравнения сплошности потока (4)
Для определения коэффициента Дарси λ надо вычислить число Рейнольдса по формуле (3)
и выяснить величину относительной шероховатости
Расчет сифонов. Сифоном называется самотечная труба, часть которой расположена выше горизонта жидкости в сосуде, который ее питает. Рассмотрим истечение из сифона под уровень. Из верхнего резервуара в нижний поступает вода по трубопроводу. Например, имеется канал и дамба, которую прокалывать не рекомендуется, поэтому трубу пускают поверху дамбы. Дано (см. рис. 49): расход Q, длины участков рассматриваемого сифона l1, l2, l3, диаметр трубы d. Труба имеет следующие местные сопротивления – сетку ζсет; первый поворот трубы ζпов 1; второй поворот ζпов 2; выход жидкости под уровень ζвых. Определить: напор H.
Рис. 49. Сифон
Для намеченных сечений будем иметь:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости, υ2 = 0,
Таким образом, имеем уравнение, аналогичное уравнению самотечной линии (113):
Пример. Определить возможную высоту расположения точки С над верхним уровнем водоема (рис. 49). Решение. Выберем плоскость 01-01 по уровню воды в верхнем резервуаре и сечение 3-3 по верхней точке С. Тогда для сечений 1-1 и 3-3:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z3 = hс, p1=pатм, p3 – давление в трубе в верхней точке С, υ1= 0 ввиду малости, υ3 – скорость в трубе,
Получаем:
Принимая во внимание, что предельное значение вакуума равно 10 м вод.ст. и учитывая наличие потерь в сифоне, а также необходимость предотвращения кавитации, которая возникает при больших понижениях давления, высоту hc не следует принимать больше 7 м.
Гидравлический удар
В напорном трубопроводе при внезапном изменении движения жидкости (мгновенная остановка или появление движения) возникает гидравлический удар, сопровождающийся резким повышением и понижением давления.
Рис. 50. К пояснению гидравлического удара
Пусть по трубе движется поток жидкости со скоростью υ. В конце трубы имеется затвор (задвижка или кран), если его внезапно закрыть, то скорость внезапно упадет до нуля. Вода сжимается, давление резко увеличивается, стенки трубопровода расширяются. Ударная волна сначала сжимается, а потом, как пружина, отталкиваясь от задвижки, идет в обратную сторону, давление падает, может упасть до рвак; а затем все повторяется в обратную сторону. Эти колебания постепенно затухают. Таким образом, при мгновенной остановке массы воды в длинном трубопроводе запас кинетической энергии должен быть куда-то израсходован. При резком повышении давления будет наблюдаться два явления: а) деформация стенок трубопровода за счет упругости материала; б) деформация жидкости при ударе (сжатие жидкости). Теоретическое обоснование явления гидравлического удара в трубах и методика его расчета была разработана Н.Е. Жуковским в 1898 г. Гидравлическим ударом называется изменение давления (понижение или повышение) в напорных трубопроводах в период неустановившегося движения жидкости (когда скорость меняется во времени). Удар распространяется по трубопроводу, как упругая волна со скоростью с, зависящей от сжимаемости жидкости и упругости стенок трубопровода. Рассмотрим прилежащую к задвижке часть объема жидкости

Рис. 51
Импульс силы, действующей в течение времени dt, равен Так как за это время dt часть объема жидкости, остановившись, потеряет количество движения
то выражения (*) и (124) можно приравнять:
так как скорость распространения ударной волны
где υ – скорость движения жидкости, с – скорость движения волны. Этой формулой пользуются в случае полного удара, кода время закрытия затвора tз меньше фазы гидравлического удара tф, т.е. tз < tф, (127) Длительность фазы гидравлического удара определяется:
где l – длина трубопровода. Если наблюдается неполный удар tз > tф, (129) то изменение давления
Скорость распространения ударной волны можно определить по формуле Жуковского:
где Напряжение в стенках трубопровода:
Скорость распространения ударной волны в воде можно подсчитать по формуле [3]:
где a – безразмерный коэффициент: для стали, железа равен 0,5, для чугуна и меди равен 1, для свинца равен 5. Исходя из формул (128) и (129) можно определить безопасное время закрытия задвижки
Меры борьбы с гидравлическим ударом. Для предохранения труб от последствий гидравлического удара необходимо принимать следующие меры: 1. Самая радикальная мера – медленное закрытие крана, то есть использовать соответствующую запорную арматуру. 2. Не допускать больших скоростей движения жидкостей по трубам. Гидравлический удар наиболее опасен в трубах малого диаметра, а так же в трубах с более высоким модулем упругости. 3. Использовать механические способы борьбы с гидравлическим ударом: а) устанавливать предохранительные клапаны, срабатывающие при увеличении давления больше допустимого; б) устанавливать на трубопроводах воздушные колпаки. Явление гидравлического удара может быть использовано в технике для подъема воды (например, в горных местностях, где для систем водоснабжения используют ключевые воды). Такая водоподъемная машина была изобретена в 1796 г. и названа «гидравлическим тараном». Пример. По стальному трубопроводу длиной l = 2 км подается вода с расходом Q =28 л/с, диаметр трубопровода d= 200 мм, толщина его стенок δ =6 мм. Определить повышение давления в трубопроводе, если в его конце будет закрыта задвижка в течение: 1)3 с; 2 ) 10 с. Решение. Определяем скорость распространения ударной волны по формуле (131):
До закрытия задвижки скорость в трубопроводе
Фаза удара определится по формуле (128):
Следовательно, в первом случае возникает полный удар, поэтому повышение давления считаем по формуле (126); а во втором – неполный удар, считаем по формуле (130). Определим повышение давления: 1) 2)
Расчет канала
Задаться надо минимум тремя значениями и таким образом, чтобы получить значение Qi, близкое к заданному, т.е. h1 принимается любое и выясняется какое получается Q1, а затем h2 назначается в сторону увеличения или уменьшения. По результатам вычислений строится график, рис. 55. По графику по заданному значению расхода Q выясняется искомая величина наполнения канала h (b). Затем для полученного h (b) определяется поформуле (167)или (168) b (h).
Рис. 55. График зависимости Q=f (h)
Решение других типов задач приводятся в гидравлических справочниках и учебниках [6, 7].
РАСЧЕТ КАНАЛОВ ЗАМКНУТОГО ПОПЕРЕЧНОГО ПРОФИЛЯ (БЕЗНАПОРНЫХ ТРУБ) Примерами каналов, имеющих замкнутый профиль (поэтому их еще называют безнапорными трубами), могут являться канализационные и дренажные трубы, гидротехнические туннели и др. Эти водостоки работают как безнапорные. Поэтому с гидравлической точки зрения они ничем не отличаются от открытых каналов. Общие сведения
Сечение труб может быть: а) круглое (канализационные коллекторы); б) овоидальное (ливневые стоки, когда в процессе эксплуатации имеются значительные колебания величины расхода); в) лотковое (так называемая ливневая канализация); г) шатровые, а также специального поперечного профиля. Уровень жидкости в таких трубах не доходит до кромки; верхняя незаполненная часть трубы называется шелыгой. Степень наполнения трубы
где h – глубина наполнения; d – диаметр круглой трубы; H – высота, если труба не круглая. Степень наполнения может меняться от нуля до единицы. В практике обычно принмают а =0,50÷0,75. (170)
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
Грунт представляет собой пористую среду. Между отдельными частицами и в трещинах породы движется вода. Такие воды принято называть грунтовыми, а их движение – фильтрацией. Укоренившийся у нас термин фильтрация равносилен понятию просачивания, т.е. медленного движения в пористой среде. Вода в поры может попасть различным образом. Например, выпадая на поверхность земли в виде дождя, она затем просачивается в грунт. На некоторой глубине такая вода может быть задержана слоем водонепроницаемого грунта (плотной глиной, скалой); при этом вода далее будет двигаться по поверхности водонепроницаемого слоя. Водонепроницаемый слой, так называемый водоупор, образует как бы русло потока грунтовой воды. В этом русле движется грунтовая вода, причем здесь получается фильтрационный поток со свободной поверхностью, в каждой точке которой имеется атмосферное давление. Такие потоки называются безнапорными (например, фильтрация воды из верхнего бьефа в нижний через земляную плотину). Напорная фильтрация наблюдается, когда водопроницаемый слой находится между двумя водонепроницаемыми (движение артезианских вод, движение грунтовой воды в вечной мерзлоте, фильтрация через бетонные плотины). Движение грунтовой воды в песках и водопроницаемых глинистых грунтах является ламинарным. Турбулентное движение грунтовой воды может получиться только в крупнозернистых грунтах (например, в гравии, гальке), а также в случае каменной наброски, трещиноватой скалы и т.п. На рис. 57 представлен случай равномерного движения. Однако обычно в практике встречаются случаи неравномерного движения, рис. 58. Неравномерность движения грунтовой воды обусловливается: 1) неправильностью формы русла; 2) уклон дна русла i ≤0; 3) в цилиндрическом русле с прямым уклоном дна каким-либо образом фиксируется глубина hф, отличная от глубины h0 равномерного движения; например, из траншеи откачивается вода, причем в траншее все время поддерживается глубина hф ≠ h0.
Рис. 57. Фильтрационный поток Рис. 58. Случай неравномерного движения Свободная поверхность фильтрационного потока называется депрессионной поверхностью; кривая же свободной поверхности АВ – кривой депрессии.
Состав грунта
Грунт следует рассматривать как единую систему, состоящую из минеральных частиц, коллоидных частиц, окружающей их воды с растворенными в ней солями и газообразной фазы (воздух, пары воды). Грунты бывают скальные и нескальные, или рыхлые. Нескальные грунты образуются путем разрушения скальных пород. Они делятся на два основных вида: грунты типа песков (несвязные), и типа глин (связные). Возьмем некоторый образец грунта объема V. Пусть объем всех пор в этом образце V |



 , м, – периметр той части поперечного сечения русла, которая смочена движущейся жидкостью.
, м, – периметр той части поперечного сечения русла, которая смочена движущейся жидкостью.
 , м. (1)
Гидродинамическое давление р, Па, – внутреннее давление движущейся жидкости, отнесенное к единице поверхности. Когда возникает движение жидкости? Вследствие перепада давлений. При этом возникают скорости.
, м. (1)
Гидродинамическое давление р, Па, – внутреннее давление движущейся жидкости, отнесенное к единице поверхности. Когда возникает движение жидкости? Вследствие перепада давлений. При этом возникают скорости.


 , а у стенок местная скорость равна нулю
, а у стенок местная скорость равна нулю  0. Введя расчетную эпюру, считают, что скорость равна по всему живому сечению своему среднему значению υ, м/с.
0. Введя расчетную эпюру, считают, что скорость равна по всему живому сечению своему среднему значению υ, м/с.
 , м3/с. (2)
, м3/с. (2)
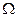 – площадь дна (или зеркала);
– площадь дна (или зеркала);  – площадь отверстия в дне;
– площадь отверстия в дне;  – начальный напор;
– начальный напор;  – конечный (после частичного опорожнения) напор.
– конечный (после частичного опорожнения) напор.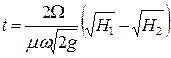 . (57)
. (57) . (58)
. (58)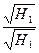 , то можно получить следующую зависимость:
, то можно получить следующую зависимость: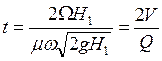 (59)
(59)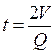 , (60)
, (60)





 .
. . (75)
. (75) .
. , (76)
, (76)
 , м3/с. (87)
, м3/с. (87) , м3/с. (88)
, м3/с. (88)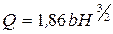 . м3/с. (89)
. м3/с. (89)

 .
. .
. (*), т.е. весь напор расходуется на преодоление сопротивлений по длине. Воспользуемся водопроводной формулой, тогда формула, помеченная (*), примет вид
(*), т.е. весь напор расходуется на преодоление сопротивлений по длине. Воспользуемся водопроводной формулой, тогда формула, помеченная (*), примет вид  (**).
(**). , (102)
, (102)
 . (103)
. (103) . (104)
. (104) . (105)
. (105)
 .
. .
.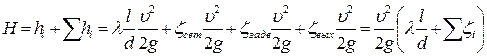 , (114)
, (114) (115)
(115) – при истечении под уровень, (116)
– при истечении под уровень, (116) – при истечении в атмосферу. (117)
– при истечении в атмосферу. (117) , (118)
, (118) . (119)
. (119) .
.
 .
.  .
. (120)
(120) (121)
(121) (122)
(122)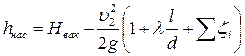 (123)
(123)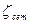 , плавный поворот трубы на 90°
, плавный поворот трубы на 90° 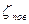 и полностью открытая задвижка
и полностью открытая задвижка  . Коэффициент гидравлического трения определить по формуле Альтшуля.
. Коэффициент гидравлического трения определить по формуле Альтшуля. 6;
6;  0,15;
0,15;  =0,15.
=0,15.
 1,02 м/с.
1,02 м/с. 2,5·105
2,5·105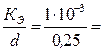 4·10-3
4·10-3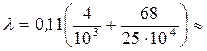 0,278
0,278 6,2 м.
6,2 м.

 .
.  .
.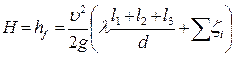

 .
.  .
.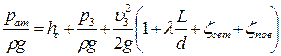 ,
, .
.
 , Так как жидкость сжимается, то остановка всей ее массы в трубопроводе не происходит одновременно. Часть объема жидкости перемещается вдоль трубы со скоростью распространения ударной волны с.
, Так как жидкость сжимается, то остановка всей ее массы в трубопроводе не происходит одновременно. Часть объема жидкости перемещается вдоль трубы со скоростью распространения ударной волны с. – давление у задвижки до закрытия,
– давление у задвижки до закрытия, 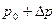 – давление у задвижки после остановки.
– давление у задвижки после остановки.
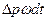 (*). Импульс – толчок, побуждение – в механике, то же, что и количество движения. Для материальной точки массы определяется выражением mυ.
(*). Импульс – толчок, побуждение – в механике, то же, что и количество движения. Для материальной точки массы определяется выражением mυ. , (124)
, (124)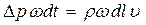 , (125)
, (125) , то повышение (понижение) давления при гидравлическом ударе в трубопроводе равно (формула Жуковского):
, то повышение (понижение) давления при гидравлическом ударе в трубопроводе равно (формула Жуковского): , (126)
, (126) , (128)
, (128) . (130)
. (130) , (131)
, (131) – модуль объемной упругости жидкости, величина, обратная коэффициенту сжимаемости, равный для холодной воды 2,06·108 Па; E – модуль упругости материала стенок трубы, равный для стали 2,06·1011 Па, для чугуна 9,81·1010 Па, для бетона (1,48÷1,96)·1010 Па; d – диаметр трубы;
– модуль объемной упругости жидкости, величина, обратная коэффициенту сжимаемости, равный для холодной воды 2,06·108 Па; E – модуль упругости материала стенок трубы, равный для стали 2,06·1011 Па, для чугуна 9,81·1010 Па, для бетона (1,48÷1,96)·1010 Па; d – диаметр трубы;  – толщина стенок трубы;
– толщина стенок трубы;  – плотность жидкости.
– плотность жидкости. . (132)
. (132)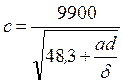 , (133)
, (133) . (134)
. (134) м/с.
м/с. м/с.
м/с. с.
с. МПа,
МПа, МПа.
МПа. , м
, м
 , м
, м
 ,
, 
 , м3/с
, м3/с

 , (169)
, (169)



