
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость фильтрации. Основной закон ламинарной фильтрации (формула Дарси)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Представим на рис. 60 металлическую трубу, заполненную песком, имеющую внутренний диаметр d. Предположим, что под действием разности давлений на концах этой трубы вода, полностью заполняющая все поры в песке, движется (фильтрует) в этих порах. Рассмотрим сечение А-А трубы, здесь можно различить три разные площади: 1) площадь сечения пор грунта ωпор, эту площадь можно рассматривать как площадь действительного «живого сечения»; 2) площадь сечения частиц грунта ωгр; через эту площадь вода в действительности не проходит; 3) площадь сечения всей трубы ωгеом; очевидно, ωгеом=

Рис. 60
Действительная скорость движения воды в порах грунта, исходя из выше сказанного, равна: υ'= где Q – расход воды, движущейся в трубе. Наряду с этим вводят понятие так называемой скорости фильтрации
Как видно, скорость фильтрации есть фиктивная (воображаемая) скорость, получающаяся в том случае, если мы себе представим, что вода движется не только через поры, но и через тельца частиц грунта, причем расход воды равен заданному (действительному расходу). Проводя опыты с фильтрацией в песках и глинах, еще в середине IXI столетия установили, что скорость фильтрации υ в случае установившегося движения может быть представлена следующей зависимостью, называемой формулой Дарси и выражающей основной закон ламинарной фильтрации: υ=kI, (181) где υ – скорость фильтрации в данной точке фильтрационного потока; I – пьезометрический уклон в той же точке (гидравлический градиент грунтового потока); k – коэффициент пропорциональности, называемый коэффициентом фильтрации. Коэффициент фильтрации, имеющий размерность скорости (т.к. I в формуле – величина безразмерная), представляет собой скорость фильтрации при уклоне I =1. Как показывают опыты, для воды определенной температуры величина k зависит только от рода грунта и характеризует фильтрационную способность грунта. Вообще же величина k зависит и от вязкости фильтрующей через грунт воды, а следовательно, и от температуры воды, поскольку с изменением температуры вязкость воды меняется. Величина k тем меньше, чем меньше частицы грунта и чем грунт более разнозернистый. Численные значения k встречаются в практике самые различные. Приведем для примера округленные численные значения k для разных грунтов (табл. 5). Расход фильтрационного потока может быть выражен такой зависимостью: Q=kωI, (182) где ω – площадь живого сечения, нормального к направлению потока.
Т а б л и ц а 5 Ориентировочные значения коэффициента фильтрации
Зависимость (182) также называется формулой Дарси. Формула (181) и (182), относящаяся к ламинарной фильтрации, имеет определенные границы применимости. Для воды обычной температуры (ν≈ 0,01 см2/с) различные авторы рекомендуют применять указанную формулу в случае, когда υd< 0,01÷0,07, υ – в м/с; d – диаметр (в см) частицы грунта (некоторого среднего размера). Если это условие не выполняется, то получаем турбулентную фильтрацию, причем зависимость Дарси нарушается. В случае широкого фильтрационного потока расчет ведут на единицу его ширины и называют удельным расходом
где h0 – глубина равномерного движения грунтовой воды
Уравнение (184) является уравнением безнапорного равномерного движения грунтовой воды в случае плоской задачи. В 1857 г. французский ученый Дюпюи, основываясь на законе Дарси, получил уравнение кривой депрессии (для фильтрационного потока со свободной поверхностью при горизонтальном подстилающем слое), рис.61:
Для двух сечений фильтрационного потока удельный расход определяется из (185) по выражению:
называемым уравнением Дюпюи, где l – расстояние между сечениями 1-1 и 2-2; h1 и h2 – глубины соответственно в сечениях 1-1 и 2-2.
Рис. 61. Схема к выводу Рис. 62. Приток грунтовой воды уравнения Дюпюи к совершенному колодцу
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.255.63 (0.006 с.) |

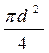 = ωпор, + ωгр. (178)
= ωпор, + ωгр. (178) ,(179)
,(179) . (180)
. (180)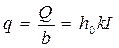 , м2/с, (183)
, м2/с, (183) . (184)
. (184)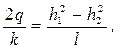 (185)
(185)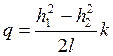 , (186)
, (186)



