
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потери напора при установившемся движении жидкостиСодержание книги
Поиск на нашем сайте
Потери напора на преодоление гидравлических сопротивлений hf (последнее слагаемое в уравнении Бернулли (17)) обычно делят на две группы: 1) потери энергии (напора) по длине потока (линейные) hl – потери, затрачиваемые на преодоление сопротивления трения; 2) местные потери энергии (напора) hj – потери, вызываемые резким изменением конфигурации границ потока. Полные потери на данном участке равны сумме всех потерь: hf= Σ hl+ Σ hj, м. (20) Потери напора (как по длине, так и местные), а также распределение скоростей по сечению потока существенно различны для ламинарного и турбулентного режима течения жидкости. Потери напора по длине как при ламинарном, так и при турбулентном режиме в трубах круглого сечения определяются по формуле Дарси-Вейсбаха:
а в открытых руслах (а также в трубах любой формы сечения) по формуле:
где λ – коэффициент сопротивления по длине; l – длина участка трубы или канала; d – диаметр трубы; υ –средняя скорость течения; C – коэффициент Шези в формуле Шези (147); R – гидравлический радиус; g – ускорение свободного падения. Коэффициент сопротивления по длине λ, его еще называют коэффициентом гидравлического трения – коэффициентом Дарси (величина безразмерная) можно определить: 1) при грубых расчетах можно принять λ = 0,03÷0,04; 2) по графику Мурина в зависимости от относительной шероховатости стенок трубы 3) по формулам, их существует больше двухсот. Наиболее универсальные следующие: - при ламинарном движении по формуле Пуазейля:
- при турбулентном режиме для трубопроводов различного назначения по формуле А.Д. Альтшуля:
- для области гидравлически гладких труб по формуле Блазиуса:
- для области квадратичного сопротивления по формуле Шифринсона:
или по формуле Маннинга:
где n – шероховатость, можно принять для водопроводных труб n = 0,012; для канализационных труб n= 0,013 [6]. Коэффициент Шези С имеет связь с коэффициентом Дарси
Потери в местных сопротивлениях. Местными называются сопротивления, вызывающие резкую деформацию потока. При обтекании турбулентным потоком какой-либо преграды происходит отрыв транзитной струи от стенки русла. При этом образуются области А (рис. 17), заполненные множеством водоворотов на участке l B, которые характеризуются возвратным течением. В сечении 2'-2' имеет место сильно деформированная эпюра осредненных скоростей.
Рис. 17. Внезапное расширение потока
Потери в местных сопротивлениях определяются по формуле Вейсбаха:
где Обычно коэффициент местного сопротивления Приведем несколько часто встречающихся случаев: 1. Внезапное расширение потока (потери на удар). На основании теоремы импульса сил была выведена формула Борда:
2. Внезапное сужение потока. При внезапном сужении (рис. 18) происходит сжатие струи (ее площадь сечения уменьшается до
Здесь ε называют коэффициентом сжатия струи. Используя зависимости (31), (35), получим величину потерь напора при внезапном сужении:
где коэффициент сопротивления внезапного сужения потока равен:
Рис. 18. Внезапное сужение потока
3. При приближенных расчетах можно принимать как средние следующие значения коэффициентов местных сопротивлений Необходимо иметь в виду, что метод нахождения потерь (суммирование потерь) имеет ограниченную область применения. Он дает правильные результаты в том случае, когда прекращается возмущающее влияние сопротивлений и поток жидкости стабилизируется. Необходимое расстояние стабилизации можно определить следующим выражением
Т а б л и ц а 1
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 , м, (21)
, м, (21) , м. (22)
, м. (22) , имеющейся в гидравлических справочниках, и режима движения Re;
, имеющейся в гидравлических справочниках, и режима движения Re; ; (23)
; (23)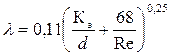 ; (24)
; (24)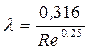 ; (25)
; (25) (26)
(26) , (27)
, (27) :
: ; (28)
; (28) ,
,  . (29)
. (29)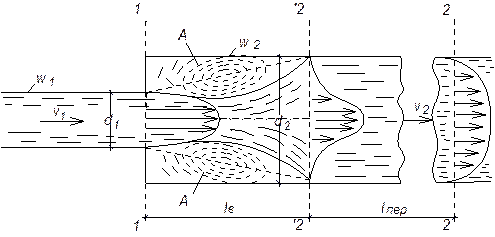
 , м,(30)
, м,(30) – коэффициент местного сопротивления, зависит от геометрии местного сопротивления и числа Рейнольдса потока; υ – средняя скорость в сечении, расположенном ниже по течению за данным сопротивлением.
– коэффициент местного сопротивления, зависит от геометрии местного сопротивления и числа Рейнольдса потока; υ – средняя скорость в сечении, расположенном ниже по течению за данным сопротивлением. ; (31)
; (31) ; (32)
; (32) . (33)
. (33) ). Площадь живого сечения струи в сжатом сечении определится:
). Площадь живого сечения струи в сжатом сечении определится: ; (34)
; (34)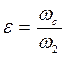 . (35)
. (35) м, (36)
м, (36) . (37)
. (37)
 .
.


