
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие указания для гидравлических расчетов трубопроводовСодержание книги
Поиск на нашем сайте
Будем рассматривать установившееся, равномерное, напорное, турбулентное движение любой жидкости в круглых цилиндрических неподвижных трубах. Гидравлический расчет трубопроводов позволяет решать три основные задачи: определять необходимый напор для пропуска известного расхода воды при заданном диаметре труб; определять пропускную способность труб заданного диаметра при известных потерях напора; определять сечение трубопроводов при заданных расходах воды и потерях напора. Общие указания для гидравлических расчетов сводятся к следующему: 1. При решении вопросов водоснабжения обычно известно расстояние l от источника водоснабжения до потребителя. 2. Расход воды Q определяется потребителем по санитарно-техническим нормам, устанавливающим количество воды на человека или на то или иное производственное предприятие. 3. Диаметр трубы d определяется по ГОСТу (после предварительных расчетов). 4. Скорость υ движения воды в трубах обычно берется в пределах (0,8÷1,5) м/с. Большие скорости движения ограничиваются по соображениям экономического порядка, так как при этом сильно возрастают эксплуатационные расходы. Большая скорость – значит, большие потери напора (в формулах (21), (22), (30) скорость стоит в квадрате). Слишком малые скорости в трубах не допускаются из-за возможности заиливания последних. 5. Потери напора hf в сети определяют мощность напорной установки или высоту водонапорной башни. 6. В напорном трубопроводе жидкость полностью заполняет сечение трубы и движется под действием разности давлений. Расчетные формулы. Гидравлические элементы живого сечения рассматриваемого потока:
площадь живого сечения: смоченный периметр: гидравлический радиус: Для расчета трубопровода исходным является уравнение Бернулли, из которого следует, что разность значений напора Н1 в 1-м сечении и напора Н2 во 2-м сечении затрачивается на преодоление гидравлических сопротивлений при движении жидкости на участке между этими сечениями. Потери напора в трубопроводе слагаются из потерь на трение по длине и потерь на преодоление местных сопротивлений по формуле (20): hf= Σ hl+ Σ hj. Потери напора по длине определяются по формуле (21): Модуль скорости W. Средняя скорость течения определится из формулы Шези (141), см. раздел 4.1
Формула для определения скорости течения потока перепишется в виде:
Следовательно, для равномерного движения модуль скорости примет еще одно, второе выражение:
Как видно, модуль скорости W представляет собой скорость υ при единичном уклоне i =1. Размерность W та же, что и υ. Модуль расхода К. Расход потока можно определить по формуле (142), см. раздел 4.1
формула перепишется в виде:
Следовательно, для равномерного движения модуль расхода
Как видно, модуль расхода К имеет два выражения (94) и (96). Из (96) следует, что К представляет собой расход Q при i =1. Из этой же формулы видно, что размерность величины К та же, что и расхода Q. Из (96) следует, что гидравлический уклон
Поскольку из формулы (19) следует, что
получаем еще одно выражение для потерь напора по длине
Понятиями модуля скорости W и модуля расхода К широко пользуются в практических расчетах труб и каналов. Для труб различного диаметра (для каналов различного сечения) и различной шероховатости п значения W и К приводятся в справочниках [6]. Потери в местных сопротивлениях определяются по формуле (30) Коэффициент Шези определяется по формуле Павловского:
или по формуле Маннинга:
Величина коэффициента шероховатости п выбирается в соответствии с материалом стенок трубопровода, в зависимости от характера обработки его внутренней поверхности, методов производства работ и эксплуатационных условий. Для ориентировочных расчетов можно приближенно принимать следующие значения коэффициента шероховатости [6]: для бетонных и железнодорожных труб……………… п = 0,0125; для металлических клепаных труб……………………. п = 0,013; для металлических сварных труб……………………… п = 0,012; для деревянных водоводов большого диаметра……… п = 0,011.
Длинные трубопроводы Простой трубопровод Напомним, что в случае длинных трубопроводов местными потерями напора пренебрегаем; кроме того, считаем, что линия Е-Е совпадает с линией Р-Р. Простой трубопровод не имеет ответвлений. Основные задачи при расчете простого длинного трубопровода. Пусть имеются два резервуара: питающий А и расходующий В с установившейся разностью уровней Н, соединенные между собой трубопроводом длиной l и постоянным диаметром d. В других случаях роль верхнего резервуара может выполнять насос, установленный в начале трубопровода и создающий там давление р=ρghA. Нижний резервуар тоже может отсутствовать, и жидкость будет вытекать в атмосферу через отверстие в конце трубопровода. Пусть резервуары открыты и давление на свободной поверхности жидкости равно атмосферному. Составим уравнение Бернулли для сечений, показанных на рис. 43.
Рис. 43. Простой длинный трубопровод одного диаметра
Для сечения 1-1: Для сечения 2-2: z1 =0, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости. υ2= 0,
Таким образом, При расчете простого трубопровода длина l его обычно известна, так же как материал и конфигурация труб. Неизвестной может быть одна из трех величин – H, Q или d. В соответствии с опытом могут быть рассмотрены три основных типа задач: 1-й тип: Дано: Q, d, l. Определить: H. Решаем по уравнению (**), предварительно находим величину K по диаметру d [6]. 2-й тип: Дано: d, l, H. Определить: Q. Решаем по уравнению (**), предварительно находим K по диаметру d [6]. 3-й тип: Дано: l, Q, H. Определить: d. По заданным l, Q, H по уравнению (**) определяем K, затем по таблицам [6] находим диаметр d. Истечение под уровень. Пьезометрическая линия Р-Р (она же Е-Е) должна иметь вид, показанный на рис. 44. Чем больше скорость в трубе, тем больше потеря напора, а следовательно, и величина I. Поэтому при d1 < d 2 пьезометрический уклон I1 должен быть больше пьезометрического уклона I2. Разность уровней жидкости в сосудах z при истечении под уровень равна потере напора:
где hl1, hl2, hl3 – потери напора по длине соответственно для 1, 2, 3-й труб, показанных на рис. 44.
Рис. 44. Простой длинный трубопровод переменного диаметра
В случае длинных труб hl определяется по формуле (99). Учитывая это, перепишем (102)
где К1, К2, К3 – модули расходов для 1, 2, 3-й труб; l1, l2, l3 – длины этих труб; Q – расход, одинаковый для всех трех труб. Вынося Q за скобки, вместо (103) получаем:
Тогда расход:
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.005 с.) |

 диаметр трубы:
диаметр трубы:  ,
, , (90)
, (90)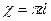 ,
,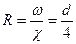 .
.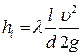 , которую можно преобразовать (будет показано далее в разделе 4.1) в формулу, вытекающую из формулы Шези:
, которую можно преобразовать (будет показано далее в разделе 4.1) в формулу, вытекающую из формулы Шези:  (22), здесь С – коэффициент Шези; l – длина потока. Можно получить еще одну формулу для определения потерь напора по длине. Для этого введем следующие понятия.
(22), здесь С – коэффициент Шези; l – длина потока. Можно получить еще одну формулу для определения потерь напора по длине. Для этого введем следующие понятия. , i – гидравлический уклон. Обозначим:
, i – гидравлический уклон. Обозначим: , (91)
, (91)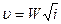 , м/с. (92)
, м/с. (92) , м/с. (93)
, м/с. (93) . Обозначим:
. Обозначим: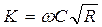 , (94)
, (94) . (95)
. (95) . (96)
. (96) . (97)
. (97) , (98)
, (98) . (99)
. (99)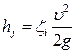 .
. (100)
(100) . (101)
. (101)
 .
. .
. (*), т.е. весь напор расходуется на преодоление сопротивлений по длине. Воспользуемся водопроводной формулой, тогда формула, помеченная (*), примет вид
(*), т.е. весь напор расходуется на преодоление сопротивлений по длине. Воспользуемся водопроводной формулой, тогда формула, помеченная (*), примет вид  (**).
(**). , (102)
, (102)
 . (103)
. (103) . (104)
. (104) . (105)
. (105)


