
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трубопровод с последовательным соединением труб разного диаметраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис. 45. Последовательное соединение труб разного диаметра
Трубопровод состоит из трех участков: d1, l1; d2, l2; d3, l3. Потери напора на каждом участке: hl1, hl2, hl3. При этом общие потери от сечения А до сечения В: (hl)АВ= Расход в трубе постоянный: Тогда по формуле (99):
Таким образом, для общего случая последовательного соединения труб
То есть систему с последовательным соединением труб можно рассматривать как один простой трубопровод, сопротивление которого равно сумме сопротивлений отдельных участков последовательно соединенных труб.
Сложный трубопровод. Параллельное соединение
Рис. 46. Параллельное соединение
Между точками А и В с пьезометрическими напорами К узлам А и В этого трубопровода (где одна подводящая труба переходит в три трубы и где эти три трубы снова переходят в одну трубу) подключим пьезометры П1 и П2. Точки А и В являются общими для каждой из трех линий соединения, и поэтому движение по любой из них происходит под одинаковой разностью напоров в начальной (А) и конечной (В) точках:
Расход же между трубопроводами должен распределяться пропорционально их пропускной способности
т.е. Причем для нескольких соединяющих линий можно написать несколько таких уравнений. Кроме того, можно записать, что сумма расходов по отдельным линиям равна общему расходу в точке А.
Выразим расходы отдельных участков через расход одного из них, например, первого (т.е. Qi разделим на Q1):
Схема решения:
Выражаем отдельные расходы через один: Подставляем полученные выражения в (*) и находим Короткие трубопроводы
Как уже отмечалось, в коротких трубопроводах потери на местных сопротивлениях соизмеримы с линейными, следовательно при расчете учитываются и hj, и hl. Расчет самотечных труб. Рассматриваем установившееся движение; разность уровней в водоемах, соединяемых трубопроводом, постоянна. Расчет сводится к определению величины расхода, используя уравнение Бернулли.
Рис. 47. Самотечная линия Пример. Вода из реки поступает в колодец по трубопроводу (затем отбирается из него насосом). Решение. Для выбранных сечений, рис. 47, будем иметь следующее:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости. υ2= 0,
H=hf, (113) то есть в самотечных линиях напор зависит от количества линейных и местных сопротивлений. Для условий нашей задачи выражение (113) примет вид
где υ – средняя скорость воды в трубе. Ее можно выразить из (114)
Обозначим первое подкоренное выражение в (115) буквой μ, этот коэффициент называется коэффициентом расхода системы, причем:
Тогда:
В самотечных линиях отложение взвешенных частиц ведет к засорению трубопровода и колодца, и поэтому трубы укладывают с уклоном в сторону водоема для промывки. Всасывающая линия насоса. Расчет обычно сводится к определению высоты установки насоса hнас. Всасывающая линия (труба) характеризуется наличием вакуума. Наибольшая величина вакуума будет непосредственно у насоса, перед его рабочим колесом (в сечении 2-2), рис. 48. И высоту установки насоса, и вакуум его можно найти, соединяя уравнением Бернулли сечение 1-1, намеченное по поверхности жидкости в колодце, и сечение 2-2, проведенное по вертикальной оси насоса. Запишем уравнение:
Рис. 48. Всасывающая труба насоса
Для сечения 1-1: Для сечения 2-2: z1 =0, z2 = hнас, p1=pатм, p2 –давление в трубе перед насосом, υ1= 0 ввиду малости, υ2 – скорость в трубе,
Получаем:
Выражение (122) показывает превышение атмосферного давления над давлением p2 в парубке у входа в насос и является вакуумом насоса или вакуумметрической высотой всасывания. Перепишем (121) с учетом (122)
Если Нвак оказывается большим, то при этом возникает кавитация, которая обусловливает снижение коэффициента полезного действия насоса. Различные типы насосов допускают различную величину вакуума. Обычно вакуум перед рабочим колесом насоса должен удовлетворять условию Нвак ≤4,0÷6,5 м вод.ст. Пример. Насос забирает воду из водоема (tводы =20°С) в количестве Q= 50 л/с. Определить максимальную высоту расположения горизонтального вала насоса над свободной поверхностью воды hнас, если давление перед насосом р2= 0,3·105 Па. На всасывающей чугунной трубе, бывшей в употреблении, диаметром d =250 мм и длиной l= 50 м имеется заборная сетка
Решение. Расход Q= 50 л/с=5·10-2 м3/с. Выпишем сведения из гидравлического справочника [6]: 1. Коэффициент кинематической вязкости для воды при температуре tводы =20°С равен ν =0,0101 см2/с=0,1·10-6 м2/с; 2. Для чугунной бывшей в употреблении трубы коэффициент эквивалентной шероховатости КЭ =1 мм; 3. Коэффициенты местных сопротивлений 4. Формула Альтшуля: Высоту постановки насоса над уровнем воды можно определить по формуле (121). Предварительно вычислим скорость воды в трубе по формуле, вытекающей из уравнения сплошности потока (4)
Для определения коэффициента Дарси λ надо вычислить число Рейнольдса по формуле (3)
и выяснить величину относительной шероховатости
Расчет сифонов. Сифоном называется самотечная труба, часть которой расположена выше горизонта жидкости в сосуде, который ее питает. Рассмотрим истечение из сифона под уровень. Из верхнего резервуара в нижний поступает вода по трубопроводу. Например, имеется канал и дамба, которую прокалывать не рекомендуется, поэтому трубу пускают поверху дамбы. Дано (см. рис. 49): расход Q, длины участков рассматриваемого сифона l1, l2, l3, диаметр трубы d. Труба имеет следующие местные сопротивления – сетку ζсет; первый поворот трубы ζпов 1; второй поворот ζпов 2; выход жидкости под уровень ζвых. Определить: напор H.
Рис. 49. Сифон
Для намеченных сечений будем иметь:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z2 =0, p1=pатм, p2=pатм, υ1= 0 ввиду малости, υ2 = 0,
Таким образом, имеем уравнение, аналогичное уравнению самотечной линии (113):
Пример. Определить возможную высоту расположения точки С над верхним уровнем водоема (рис. 49). Решение. Выберем плоскость 01-01 по уровню воды в верхнем резервуаре и сечение 3-3 по верхней точке С. Тогда для сечений 1-1 и 3-3:
Для сечения 1-1: Для сечения 2-2: z1 = Н, z3 = hс, p1=pатм, p3 – давление в трубе в верхней точке С, υ1= 0 ввиду малости, υ3 – скорость в трубе,
Получаем:
Принимая во внимание, что предельное значение вакуума равно 10 м вод.ст. и учитывая наличие потерь в сифоне, а также необходимость предотвращения кавитации, которая возникает при больших понижениях давления, высоту hc не следует принимать больше 7 м.
Гидравлический удар
В напорном трубопроводе при внезапном изменении движения жидкости (мгновенная остановка или появление движения) возникает гидравлический удар, сопровождающийся резким повышением и понижением давления.
Рис. 50. К пояснению гидравлического удара
Пусть по трубе движется поток жидкости со скоростью υ. В конце трубы имеется затвор (задвижка или кран), если его внезапно закрыть, то скорость внезапно упадет до нуля. Вода сжимается, давление резко увеличивается, стенки трубопровода расширяются. Ударная волна сначала сжимается, а потом, как пружина, отталкиваясь от задвижки, идет в обратную сторону, давление падает, может упасть до рвак; а затем все повторяется в обратную сторону. Эти колебания постепенно затухают.
Таким образом, при мгновенной остановке массы воды в длинном трубопроводе запас кинетической энергии должен быть куда-то израсходован. При резком повышении давления будет наблюдаться два явления: а) деформация стенок трубопровода за счет упругости материала; б) деформация жидкости при ударе (сжатие жидкости). Теоретическое обоснование явления гидравлического удара в трубах и методика его расчета была разработана Н.Е. Жуковским в 1898 г. Гидравлическим ударом называется изменение давления (понижение или повышение) в напорных трубопроводах в период неустановившегося движения жидкости (когда скорость меняется во времени). Удар распространяется по трубопроводу, как упругая волна со скоростью с, зависящей от сжимаемости жидкости и упругости стенок трубопровода. Рассмотрим прилежащую к задвижке часть объема жидкости

Рис. 51
Импульс силы, действующей в течение времени dt, равен Так как за это время dt часть объема жидкости, остановившись, потеряет количество движения
то выражения (*) и (124) можно приравнять:
так как скорость распространения ударной волны
где υ – скорость движения жидкости, с – скорость движения волны. Этой формулой пользуются в случае полного удара, кода время закрытия затвора tз меньше фазы гидравлического удара tф, т.е. tз < tф, (127) Длительность фазы гидравлического удара определяется:
где l – длина трубопровода. Если наблюдается неполный удар tз > tф, (129) то изменение давления
Скорость распространения ударной волны можно определить по формуле Жуковского:
где
Напряжение в стенках трубопровода:
Скорость распространения ударной волны в воде можно подсчитать по формуле [3]:
где a – безразмерный коэффициент: для стали, железа равен 0,5, для чугуна и меди равен 1, для свинца равен 5. Исходя из формул (128) и (129) можно определить безопасное время закрытия задвижки
Меры борьбы с гидравлическим ударом. Для предохранения труб от последствий гидравлического удара необходимо принимать следующие меры: 1. Самая радикальная мера – медленное закрытие крана, то есть использовать соответствующую запорную арматуру. 2. Не допускать больших скоростей движения жидкостей по трубам. Гидравлический удар наиболее опасен в трубах малого диаметра, а так же в трубах с более высоким модулем упругости. 3. Использовать механические способы борьбы с гидравлическим ударом: а) устанавливать предохранительные клапаны, срабатывающие при увеличении давления больше допустимого; б) устанавливать на трубопроводах воздушные колпаки. Явление гидравлического удара может быть использовано в технике для подъема воды (например, в горных местностях, где для систем водоснабжения используют ключевые воды). Такая водоподъемная машина была изобретена в 1796 г. и названа «гидравлическим тараном». Пример. По стальному трубопроводу длиной l = 2 км подается вода с расходом Q =28 л/с, диаметр трубопровода d= 200 мм, толщина его стенок δ =6 мм. Определить повышение давления в трубопроводе, если в его конце будет закрыта задвижка в течение: 1)3 с; 2 ) 10 с. Решение. Определяем скорость распространения ударной волны по формуле (131):
До закрытия задвижки скорость в трубопроводе
Фаза удара определится по формуле (128):
Следовательно, в первом случае возникает полный удар, поэтому повышение давления считаем по формуле (126); а во втором – неполный удар, считаем по формуле (130). Определим повышение давления: 1) 2)
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 899; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.25 (0.014 с.) |


 . (106)
. (106)
 , где К=f(d) определяется по [6]. Следовательно:
, где К=f(d) определяется по [6]. Следовательно: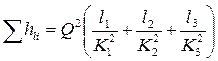 . (107)
. (107)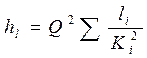 . (108)
. (108)
 и
и  проходит несколько линий труб, образуя так называемое параллельное соединение. В этом случае формула (106) оказывается неприменимой: потери напора в отдельных трубах при параллельном их соединении складывать нельзя.
проходит несколько линий труб, образуя так называемое параллельное соединение. В этом случае формула (106) оказывается неприменимой: потери напора в отдельных трубах при параллельном их соединении складывать нельзя. . (109)
. (109) , (110)
, (110) ,
,  ,
,  и т.д.
и т.д. . (111)
. (111) . (112)
. (112)
 ,
, 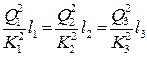 ,
,  .
. ,
,  .
. ,
,  ,
,  и
и  .
.
 .
. .
.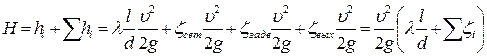 , (114)
, (114) (115)
(115) – при истечении под уровень, (116)
– при истечении под уровень, (116) – при истечении в атмосферу. (117)
– при истечении в атмосферу. (117) , (118)
, (118) . (119)
. (119) .
.
 .
.  .
. (120)
(120) (121)
(121) (122)
(122)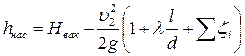 (123)
(123)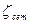 , плавный поворот трубы на 90°
, плавный поворот трубы на 90° 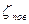 и полностью открытая задвижка
и полностью открытая задвижка  . Коэффициент гидравлического трения определить по формуле Альтшуля.
. Коэффициент гидравлического трения определить по формуле Альтшуля. 6;
6;  0,15;
0,15;  =0,15.
=0,15.
 1,02 м/с.
1,02 м/с. 2,5·105
2,5·105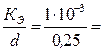 4·10-3
4·10-3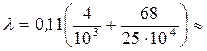 0,278
0,278 6,2 м.
6,2 м.

 .
.  .
.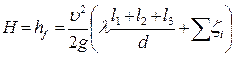

 .
.  .
.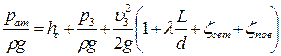 ,
, .
.
 , Так как жидкость сжимается, то остановка всей ее массы в трубопроводе не происходит одновременно. Часть объема жидкости перемещается вдоль трубы со скоростью распространения ударной волны с.
, Так как жидкость сжимается, то остановка всей ее массы в трубопроводе не происходит одновременно. Часть объема жидкости перемещается вдоль трубы со скоростью распространения ударной волны с. – площадь поперечного сечения трубы, Vж=ω·dl – рассматриваемый объем жидкости,
– площадь поперечного сечения трубы, Vж=ω·dl – рассматриваемый объем жидкости,  – давление у задвижки до закрытия,
– давление у задвижки до закрытия, 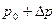 – давление у задвижки после остановки.
– давление у задвижки после остановки.
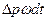 (*). Импульс – толчок, побуждение – в механике, то же, что и количество движения. Для материальной точки массы определяется выражением mυ.
(*). Импульс – толчок, побуждение – в механике, то же, что и количество движения. Для материальной точки массы определяется выражением mυ. , (124)
, (124)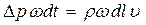 , (125)
, (125) , то повышение (понижение) давления при гидравлическом ударе в трубопроводе равно (формула Жуковского):
, то повышение (понижение) давления при гидравлическом ударе в трубопроводе равно (формула Жуковского): , (126)
, (126) , (128)
, (128) . (130)
. (130) , (131)
, (131) – модуль объемной упругости жидкости, величина, обратная коэффициенту сжимаемости, равный для холодной воды 2,06·108 Па; E – модуль упругости материала стенок трубы, равный для стали 2,06·1011 Па, для чугуна 9,81·1010 Па, для бетона (1,48÷1,96)·1010 Па; d – диаметр трубы;
– модуль объемной упругости жидкости, величина, обратная коэффициенту сжимаемости, равный для холодной воды 2,06·108 Па; E – модуль упругости материала стенок трубы, равный для стали 2,06·1011 Па, для чугуна 9,81·1010 Па, для бетона (1,48÷1,96)·1010 Па; d – диаметр трубы;  – толщина стенок трубы;
– толщина стенок трубы;  – плотность жидкости.
– плотность жидкости. . (132)
. (132)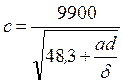 , (133)
, (133) . (134)
. (134) м/с.
м/с. м/с.
м/с. с.
с. МПа,
МПа, МПа.
МПа.


