
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлический расчет простых и сложных напорных трубопроводов при изотермическом режиме теченияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гидравлический расчет трубопроводов при движении по ним однофазных жидкостей сводится обычно к определению или диаметра D, или начального давления р1, или пропускной способности Q по известным формулам общей гидравлики. Основой гидравлических расчетов трубопроводов является известное уравнение Бернулли:
Каждый член уравнения в скобках имеет размерность высоты: z –геометрические отметки различных точек линии тока над плоскостью сравнения (геометрический напор); p/(rg)- пьезометрический напор; v2/2g – скоростной напор. Сумма z + p/(rg) называется потенциальным напором. Сумма всех трех слагаемых называется полным напором жидкости в данном живом сечении. С энергетической точки зрения слагаемые уравнения Бернулли представляют собой удельную (приходящуюся на единицу веса жидкости) энергию: [z +p/(rg)]-удельная потенциальная энергия; v2/(2g) – удельная кинетическая энергия. При движении жидкостей по трубам энергия расходуются в основном на преодоление сил трения hтр и местных сопротивлений hм.с в трубопроводах (задвижки, вентили, колена и т. д.). Определение потерь напора на трение. Потери напора на преодоление сил трения hтр по длине трубопровода круглого сечения определяются по формуле Дарси-Вейсбаха:
или
где hтр – потери напора на преодоление сил трения, м;
где Если течение в трубе ламинарное, (Re<2300), то коэффициент гидравлического сопротивления не зависит от шероховатости трубы и равен
Здесь
где Q – расход жидкости, м3/с; При турбулентном течении жидкости (Re>2800) для определения Для переходного и смешанного режима (числа Рейнольдса от 2800 до 105)
Для квадратичного режима движения
Определение гидравлического уклона. Гидравлический уклон характеризует потерю напора на единицу длины трубопровода, т. е. согласно (2.2)
Подставив в (2.8) значения для ламинарного режима
для турбулентного режима
В результате получается: для ламинарного режима
для турбулентного режима
где D, см,
Потери напора на трение по всей длине трубопровода определяются по формуле:
Пример 1. По трубопроводу с внутренним диаметром 100 мм и длиной 3 км подается нефть в количестве 200 т/сут., плотностью Решение. Вначале определяем скорость нефти (м/с):
Режим движения нефти определяется по (2.5)
т. е. режим ламинарный. Коэффициент гидравлического сопротивления
Перепад давления (в Па) найдем, используя формулу (2.3),
Перепад давления, выраженный в кгс/см2 (1 кгс/см2=9,81.104 Па)
Перепад давления, выраженный в м,
Определение потерь напора на местные сопротивления. К местным сопротивлениям относятся сопротивления в закруглениях труб, резких поворотах, отводах, кранах, вентилях, задвижках, клапанах и т. д. Местные сопротивления необходимо учитывать при расчете всасывающих линий (имеющих небольшую длину) насосов и компрессоров. При больших длинах напорных трубопроводов удельный вес местных сопротивлений обычно невелик и ими часто пренебрегают при расчетах. Потери напора на местные сопротивления hм.с находятся по формуле
Здесь v – средняя скорость движения жидкости в сечении потока за местным сопротивлением; В большинстве случаев удобнее определять местные сопротивления по так называемой эквивалентной длине (длина прямого участка трубопровода данного диаметра, на которой потеря напора на трение по длине hтр эквивалентна потере напора hм.с, вызываемой данным местным сопротивлением). Эквивалентная длина l э определяется по формуле Дарси-Вейсбаха
и по формуле (2.14). Приравнивая между собой правые части формул (2.14) и (2.15)
получаем
Значения местных сопротивлений определяются из справочников. Полный перепад давления в "рельефных" (не горизонтальных) трубопроводах определяется по формуле
где hтр и hм.с – соответственно потери напора на трение (путевые потери) и местные сопротивления, определяемые по (2.2) и (2.4); Короткие трубопроводы (всасывающие линии насосов) также рассчитываются по формуле (2.17), только вместо разности геодезических отметок В некоторых случаях возникает необходимость в графическом поверочном расчете, который позволяет определить давление в любой точке трубопровода. В этом случае строится в сжатом масштабе продольный профиль трубопровода, с совмещением начальных точек напорного трубопровода с отметкой оси насоса (точка А на рис. 2.1). Точка С – конечная точка трубопровода, соответствующая, например, отметке дна резервуара. Точка D – отметка верхнего уровня жидкости в резервуаре.
Рис.2.1. Расчетная схема простого напорного трубопровода сложного профиля
По вертикальной линии от оси насоса А откладывается в масштабе поперечного профиля общий напор H, определяемый по (2.17). Проведя горизонтальную линию, соответствующую уровню в резервуаре, получим точку а. Отрезок Аа соответствует разности геодезических отметок между осью насоса и верхним уровнем в резервуаре (zн – zк), а отрезок аВ – напору, идущему на преодоление гидравлических сопротивлений в трубопроводе hтр. Соединив точки В и D прямой линией, получим гидравлический уклон, определяемый формулой (2.8). Для определения напора в любой точке трубопровода (пунктир) необходимо из этой точки провести вертикальную линию до линии гидравлического уклона BD. Измеряя, например, линию Km и умножая результат замера на поперечный масштаб, получим значение напора в данной точке трубопровода. В точке К трубопровода напор будет больше напора, развиваемого насосом. Построение таких графиков позволяет выявить участки трубопровода с минимальными и максимальными напорами, что необходимо знать при расчете трубопровода на прочность. При определении гидравлического уклона или тангенса угла Гидравлический расчет простого напорного трубопровода (постоянного диаметра и без ответвлений), транспортирующего жидкость в однофазном состоянии, сводится к определению одного из следующих параметров: 1) пропускной способности трубопровода Q; 2) необходимого начального давления р1; 3) диаметра трубопровода D. При этом физические свойства перекачиваемой жидкости – плотность В задачах первого типа искомой является пропускная способность трубопровода Q. Коэффициент гидравлического сопротивления Сначала задаются несколькими произвольными значениями расхода жидкости Q. Затем определяют скорость потока (
пренебрегая при этом скоростным напором
Рис. 2.2. Расчетные схемы простых трубопроводов
В задачах второго типа в зависимости от числа Рейнольдса, которое в данном случае легко определяется по известным диаметру трубопровода D и расходу жидкости Q, находят В задачах третьего типа искомым является диаметр нефтепровода D при известном расходе жидкости Q, перепаде давлений Здесь, как и в задаче первого типа, Необходимый диаметр трубопровода определяется по кривой (см. рис. 2.2, б) по заданному напору
Если такого диаметра труб в стандартах нет, то принимается ближайший наибольший диаметр. Пример 2. 0пределить пропускную способность нефтепровода, если Решение. В связи с тем, что Произвольные расходы нефти, соответствующие им скорости, а также коэффициенты гидравлического сопротивления и потери напора представлены ниже. На рис.2.3 показана кривая зависимости hп=f(Q),построенная по приведенным ниже данным.
Рис. 2.3. Зависимость hп=f(Q)
Перепад давления Разность геодезических отметок Перепад давления за счет разности геодезических отметок
Общий перепад давления р= 10+3,22= 13,22 кгс/см2 = 132,2 м вод. ст. На рис. 2.3 в масштабе проведена горизонтальная линия до кривой hп=f(Q) и из точки пересечения на ось расходов Q восставлен перпендикуляр. Таким образом, пропускная способность нефтепровода получалась равной 23 л/с. Сложный трубопровод представляет собой несколько последовательно или параллельно соединенных простых трубопроводов, и поэтому гидравлический расчет его в принципе ничем не отличается от расчета по изложенной расчетной схеме. Здесь мы рассмотрим расчет графическим способом сборного коллектора, транспортирующего однофазную жидкость. По схеме (рис. 2.4) к коллектору AD длиной L подсоединены три групповые замерные установки в точках А, В и С. Пусть в этих точках в коллектор поступает нефть в количестве Q1, Q2 и Q3, т/сут.
Рис. 2.4. Расчетная схема сложного нефтепровода
Предварительно задавшись диаметром трубопровода, определим среднюю скорость движения нефти на участке коллектора АВ из равенства
где Зная среднюю скорость нефти, диаметр D и задавшись вязкостью нефти Допустим, что Re<2300, т. е. режим ламинарный. Тогда согласно формуле (2.9) гидравлический уклон на данном участке равен
Необходимый напор в точке А, согласно формуле (2.13), будет
В точке В в коллектор поступает дополнительное количество нефти Q2. Таким образом, по участку коллектора ВС необходимо перекачать нефть в количестве Q1+Q2. Гидравлический уклон на участке ВС
Необходимый напор на участке ВС
Для свободного движения нефти в количестве Q1+Q2 на участке ВС необходимо, чтобы напор в точке А был равен hА+hВ. Графически этот напор определится, если из точки b провести линию ba2, параллельную а1В. Также подсчитывается гидравлический уклон на участке CD для расхода жидкости Q1+Q2+Q3
и определяется суммарный гидравлический напор участка
Данная задача значительно усложнится, если на отдельных участках трубопровода А – D, в местах подсоединения сборных коллекторов B и C, будут турбулентные, а не ламинарные, режимы. При последовательном соединении простых трубопроводов, имеющих различные диаметры, расход нефти или воды на всем пути остается постоянным, а общие потери напора определяются сложением потерь напора на отдельных участках. При параллельном соединении трубопроводов разность напоров на концах участков будет одинакова, т. е. потери напора выражаются формулой
а сумма расходов в параллельных ветвях равна общему расходу
2.3 Гидравлический расчет трубопроводов при движении в них нефтегазовых смесей Большинство промысловых нефтепроводов работает с неполным заполнением сечения трубы нефтью, т. е. часть объема трубы обычно бывает занята газом. Ниже приводятся основные понятия и определения, относящиеся к двухфазным потокам, а также некоторые указания к расчету нефтепроводов, транспортирующих двухфазную смесь. Основная сложность расчета заключается в том, что в газожидкостном потоке происходит относительное движение фаз, обусловленное их различными плотностью и вязкостью, т. е., иными словами, имеет место скольжение этих фаз. На рис. 2.5 приведены некоторые структуры потока в горизонтальных трубах при движении в них воздушно-водяных смесей.
Рис. 2.5. Структуры газожидкостных потоков в горизонтальных трубах. Потоки: а – с пузырьками газа в верхней образующей; б – с началом образования газовых пробок; в – расслоенный; г – волновой; д – пробковое течение; е – эмульсионный (сотовый); ж – пленочный.
Основная задача, возникающая при гидравлическом расчете трубопроводов, транспортирующих газожидкостную смесь, это определение перепадов давления. Основное расчетное уравнение для "рельефных" (не горизонтальных) нефтепроводов упрощенном виде записывается так:
где
Перепад давления, обусловленный гидравлическим сопротивлением газожидкостного потока, определяется по формуле, подобной формуле Дарси-Вейсбаха (2.3):
где при Reсм<2300
при Re>2300
Число Рейнольдса для смеси определяется как
Кинематическая вязкость двухфазного потока
где
где Vг и Qж – соответственно объемные расходы газа и жидкости при средних давлении и температуре в трубопроводе. Плотность газожидкостной смеси
где
Истинное газосодержание Доля сечения потока, занятая жидкой фазой, соответственно составит
В (2.23) входит средняя скорость газожидкостной смеси, которая определяется из выражения
Общий перепад давления в "рельефном" трубопроводе (в Па), обусловленный гравитационными силами (геодезическими отметками) и силами трения смеси, определяется из уравнения (2.21)
где zп и zсп – высоты отдельных восходящих (подъемов) и нисходящих (спусков) участков трубопровода, м;
При восходящем потоке
при нисходящем потоке
После подстановки в уравнение (2.33) выражения (2.23) получим общий перепад
Данное выражение является основным расчетным уравнением при проектировании нефтепроводов, работающих при неполном заполнении сечения трубы нефтью.
2.4 Основные понятия о реологических свойствах нефти и расчет трубопроводов, транспортирующих неньютоновские жидкости Разрабатывается много месторождений с парафинистой нефтью, движение которой по трубам не подчиняется известным законам гидравлики. Транспортировка таких нефтей по трубопроводам имеет свою специфику и связана с большими трудностями. Если вязкость парафинистой нефти значительно возрастает из-за понижения температуры, то существенно осложняется пуск нефтепровода после его остановки, а при перекачке парафинистых нефтей может произойти "замораживание" нефтепровода до полного прекращения подачи. При перекачке высоковязких нефтей возникает необходимость увеличения мощности перекачивающих агрегатов, использования путевых подогревателей, или увеличения диаметра нефтепровода или использования различных реагентов. Для улучшения прокачиваемости парафинистых нефтей с высокой температурой застывания применяют растворители (керосин, углеводородный конденсат, а также депрессорные присадки или депресаторы, введение которых существенно улучшает реологические свойства нефти. Характерной особенностью парафинистой нефти является зависимость изменения вязкости от перепада давления Под реологическими свойствами нефти понимается зависимость вязкости нефти Согласно закону Ньютона о вязкостном трении при движении жидкости в круглой трубе, уравнение касательного напряжения
где
Рис. 2.6 Движение ньютоновских и неньютоновских жидкостей по трубам: а – модель течения жидкости; б – распределение напряжений и скоростей в структурном потоке; в – зависимость напряжений сдвига от градиента скорости для ньютоновских 1 и неньютоновских 2, 3 жидкостей
Формулу (2.38) можно представить в виде:
Зависимость имеет вид прямой, выходящей из начала координат (рис. 2.6,в, поз. 1), тангенс угла которой к оси ординат является постоянной величиной и характеризует абсолютную вязкость нефти. Жидкости, вязкость которых изменяется по прямолинейному закону ( Жидкости, вязкость которых изменяется в зависимости от напряжения сдвига и градиента скорости ( Вязкость неньютоновских жидкостей определяется по уравнению Шведова-Бингема:
или
где Рассмотрим течение в трубе заштрихованного объема жидкости (рис. 2.6, a) длиной l и диаметром D при приложении внешней силы F. Давление на концах трубопровода пусть будет p1 и р2. Внешняя сила F нарушит условия равновесия сил давления
F>Fтр
или
Сокращая, получим
Предельному равновесию, т.е. такому состоянию, когда неньютоновская жидкость только начнет двигаться, будет соответствовать условие
Таким образом, если
то жидкость в трубопроводе будет двигаться, и в зависимости от приложенной разности давлений могут образоваться три различных режима ее движения: структурный, ламинарный или турбулентный. Под структурным режимом понимается такой режим, когда движение всего потока "жидкости" условно принимается за движение твердого тела с одинаковой скоростью по всему поперечному сечению. По мере увеличения перепада давления Теперь установим закон распределения скоростей в поперечном сечении трубы при ламинарно-структурном режиме. Будем исходить из общего уравнения (2.39) для касательного напряжения в неньютоновской жидкости. Для любого цилиндрического слоя жидкости радиусом (см. рис.2.6,б) r>r0 касательное напряжение
где d – диаметр цилиндрического слоя жидкости, в котором напряжение сдвига равно Подставив последнее значение
Умножим обе части этого уравнения на dr:
Проинтегрировав данное выражение
получим
Постоянная интегрирования С находится из условия: у стенок трубы при r=R, v=0, следовательно,
Подставив (2.47) в (2.46) получим
Кривая скоростей, соответствующая этой формуле, представлена на рис. 2.6, б. Она состоит из двух частей: параболических ветвей у стенок трубы, соответствующих ламинарному режиму течения, и прямолинейного участка в центральном ядре, соответствующего структурному режиму течения. Для определения скорости движения центрального ядра в формуле (2.48) необходимо принять r = r0. Тогда
Расход жидкости при ламинарно-структурном режиме будет равен
где Qл и Qц – соответственно расход в ламинарном кольце и в центральном ядре. Последнее выражение можно представить как
где v и v0 – скорости жидкости, определяемые из выражений (2.48) и (2.49). Подставив в выражение (2.50) формулы (2.48), (2.49) b проведя затем интегрирование и некоторые упрощения, получим формулу Букингема:
При больших перепадах давлений последним членом в этом уравнении можно пренебречь ввиду его малости, и тогда формула (2.51) принимает вид:
где Часто пользуются формулой Букингема следующего вида
Так как касательные напряжения в трубе имеют линейный характер (см. рис. 2.6,б), то на поверхности ядра они равны
откуда
Пример 3. Определить напряжение сдвига в плоскости ядра, находящегося на расстоянии r0=25 мм от стенки трубы диаметром D = 100 мм при перекачке парафинистой нефти со средней скоростью, равной 0,1 м/с. Плотность нефти Решение. Определим режим движения
Перепад давления на единицу длины трубопровода (в Па/м) определим по формуле (2.53), пренебрегая в ней членом, заключенным в квадратные скобки, ввиду его малости
или
Максимальное касательное напряжение (в Па), возникающее у стенки трубы, определится по формуле (2.42)
Касательное напряжение (в Па) на поверхности ядра определится по формуле (2.54)
Пример 4. Определить подачу выкидной линии для условий примера 3, если длина ее 20 м и перепад давления на этой длине
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.014 с.) |

 (2.1)
(2.1) (2.2)
(2.2) , (2.3)
, (2.3) – потери давления, Па; l – длина трубопровода, м; D – диаметр трубопровода, м;
– потери давления, Па; l – длина трубопровода, м; D – диаметр трубопровода, м; 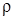 – плотность жидкости, кг/м3; v – средняя скорость течения жидкости, м/с; Q – расход жидкости, м3/с; g – ускорение свободного падения, м/с2;
– плотность жидкости, кг/м3; v – средняя скорость течения жидкости, м/с; Q – расход жидкости, м3/с; g – ускорение свободного падения, м/с2;  – коэффициент гидравлического сопротивления (безразмерный), в общем случае зависящий от числа Рейнольдса (Re) и относительной шероховатости, т. е.
– коэффициент гидравлического сопротивления (безразмерный), в общем случае зависящий от числа Рейнольдса (Re) и относительной шероховатости, т. е.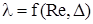 ,
, – абсолютная шероховатость трубы, см; D – диаметр трубопровода, см.
– абсолютная шероховатость трубы, см; D – диаметр трубопровода, см.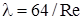 . (2.4)
. (2.4) , (2.5)
, (2.5) – площадь сечения трубы, м2;
– площадь сечения трубы, м2;  –кинематическая вязкость жидкости, м2/с; D – внутренний диаметр трубопровода, м;
–кинематическая вязкость жидкости, м2/с; D – внутренний диаметр трубопровода, м;  – динамическая вязкость жидкости, Па.с.
– динамическая вязкость жидкости, Па.с. . (2.6)
. (2.6) . (2.7)
. (2.7) . (2.8)
. (2.8)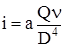 ; (2.9)
; (2.9) . (2.10)
. (2.10) ;
;  ; (2.11)
; (2.11)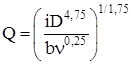 ;
;  , (2.12)
, (2.12) . (2.13)
. (2.13) .
. ,
, .
. .
.
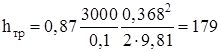 .
. . (2.14)
. (2.14) – коэффициент местного сопротивления, зависящий от Re, формы местного сопротивления и шероховатости, а для запорных устройств – от степени их открытия.
– коэффициент местного сопротивления, зависящий от Re, формы местного сопротивления и шероховатости, а для запорных устройств – от степени их открытия. (2.15)
(2.15) ,
, . (2.16)
. (2.16) (2.17)
(2.17) разность геодезических отметок в м: плюс ставится тогда, когда сумма участков подъема (zп) трубопровода больше суммы участков спуска (zсп), минус—в обратном случае (рис. 2.1); zн и zк – соответственно геодезические отметки начала и конца трубопровода.
разность геодезических отметок в м: плюс ставится тогда, когда сумма участков подъема (zп) трубопровода больше суммы участков спуска (zсп), минус—в обратном случае (рис. 2.1); zн и zк – соответственно геодезические отметки начала и конца трубопровода. принимается разность уровней вала насоса и жидкости в резервуаре.
принимается разность уровней вала насоса и жидкости в резервуаре.
 необходимо потери напора hтр делить на длину трубопровода l (пунктирная линия), а не на его проекцию L.
необходимо потери напора hтр делить на длину трубопровода l (пунктирная линия), а не на его проекцию L.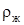 и вязкость
и вязкость  а также разность геодезических отметок (
а также разность геодезических отметок ( ). Далее рассчитывают режим движения (
). Далее рассчитывают режим движения ( ) и в зависимости от него определяют
) и в зависимости от него определяют  ,
, ввиду его малости.
ввиду его малости.
 .
. =800 кг/м3;
=800 кг/м3; 
 .
.
 , (2.18)
, (2.18)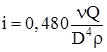 .
. .
. .
. .
.
 .
. , (2.19)
, (2.19) . (2.20)
. (2.20)
 , (2.21)
, (2.21) – перепад давления, обусловленный весом столба газожидкостной смеси, а для горизонтального трубопровода формула (2.19) запишется следующим образом
– перепад давления, обусловленный весом столба газожидкостной смеси, а для горизонтального трубопровода формула (2.19) запишется следующим образом . (2.22)
. (2.22) , (2.23)
, (2.23) – коэффициент гидравлического сопротивления, находится следующим образом:
– коэффициент гидравлического сопротивления, находится следующим образом: ; (2.24)
; (2.24) . (2.25)
. (2.25) . (2.26)
. (2.26) определяется по формуле Манна:
определяется по формуле Манна: , (2.27)
, (2.27) – расходное объемное газосодержание двухфазною потока, определяемое по формуле
– расходное объемное газосодержание двухфазною потока, определяемое по формуле , (2.28)
, (2.28) , входящая в формулу (2.23), определяется из выражения
, входящая в формулу (2.23), определяется из выражения (2.29)
(2.29) – плотность жидкости и газа при средних давлении и температуре смеси в трубопроводе;
– плотность жидкости и газа при средних давлении и температуре смеси в трубопроводе;  – истинное газосодержание определяется как отношение мгновенной площади сечения потока, занятого газовой фазой Fг, к полному поперечному сечению потока F, т. е.
– истинное газосодержание определяется как отношение мгновенной площади сечения потока, занятого газовой фазой Fг, к полному поперечному сечению потока F, т. е. . (2.30)
. (2.30) . (2.31)
. (2.31) . (2.32)
. (2.32)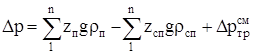 , (2.33)
, (2.33) и
и  – истинная плотность смеси соответственно на восходящих и нисходящих участках, определяемая по истинному объемному газосодержанию:
– истинная плотность смеси соответственно на восходящих и нисходящих участках, определяемая по истинному объемному газосодержанию: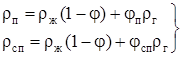 . (2.34)
. (2.34) ; (2.35)
; (2.35) . (2.36)
. (2.36) . (2.37)
. (2.37) ) и от изменения градиента скорости в трубе dv/dr.
) и от изменения градиента скорости в трубе dv/dr. , (2.38)
, (2.38)
 .
.
 const), называются неньютоновскими (кривые 2 и 3 на рис.2.6,в). Кривые этого типа обычно можно снять при температуре застывания нефти.
const), называются неньютоновскими (кривые 2 и 3 на рис.2.6,в). Кривые этого типа обычно можно снять при температуре застывания нефти. (2.39)
(2.39) ,
, – минимальное касательное напряжение, превышение которого вызывает текучесть ядра неньютоновской жидкости, Па;
– минимальное касательное напряжение, превышение которого вызывает текучесть ядра неньютоновской жидкости, Па;  и силы трения
и силы трения  , возникающей на внутренней поверхности трубы при движении жидкости, если
, возникающей на внутренней поверхности трубы при движении жидкости, если . (2.40)
. (2.40) . (2.41)
. (2.41) . (2.42)
. (2.42) , (2.43)
, (2.43) , (2.44)
, (2.44) . (2.45)
. (2.45) .
. ,
, . (2.46)
. (2.46) . (2.47)
. (2.47) . (2.48)
. (2.48) . (2.49)
. (2.49) ,
,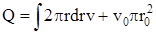 , (2.50)
, (2.50) . (2.51)
. (2.51) , (2.52)
, (2.52) – перепад давления, соответствующий началу движения жидкости, определяемый по формуле (2.42).
– перепад давления, соответствующий началу движения жидкости, определяемый по формуле (2.42). . (2.53)
. (2.53) ,
, . (2.54)
. (2.54) – ламинарный.
– ламинарный.
 .
. .
. .
.


