
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлический расчет систем трубопроводов сбора газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Перемещение газа по трубе по сравнению с перемещением по ней нефти характеризуется рядом важных особенностей, являющихся результатом различия их физических свойств. Вследствие гидравлических сопротивлений, имеющих место при движении газа по трубе, происходит непрерывное снижение давления, которое в большинстве случаев бывает больше атмосферного в начале трубы. В результате снижения давления происходит расширение газа, его удельный объем увеличивается, а плотность, наоборот, уменьшается. Если движение установившееся, то массовый расход газа G в силу неразрывности движения остается неизменным, объемный же расход Q будет увеличиваться по длине трубы, вследствие чего величина объемной скорости газа повышается. При расширении газа и явлений теплообмена будет иметь место также и непрерывное изменение температуры газа по длине трубы. Однако в большинстве случаев оказывается вполне возможным принять температуру постоянной, считая, что процесс расширения газа происходит изотермически. При этом величина динамической вязкости газа будет сохраняться почти постоянной. В нефтепромысловой практике приходится определять гидравлические параметры газопровода, т. е. расход, диаметр, начальное и конечное давления. Исходным уравнением для гидравлического расчета газопроводной трубы при перемещении по ней газа является уравнение Дарси-Вейсбаха
Для элемента трубы оно будет иметь вид
Обозначим линейную скорость через массовый расход
где S – площадь поперечного сечения потока газа. При этом равенство (2.73) примет вид
Для изотермического перемещения газа
где р0 – атмосферное давление; Подставив значение
отсюда следует
и после замены
Коэффициент гидравлического сопротивления
Другие формулы менее удобны, например ВНИИгаза
Неудобство формулы ВНИИгаза состоит в том, что в ней необходимо дополнительно вычислять объемную скорость движения и вязкость газа. В формуле Панхендлакоэффициент Преимущественное распространение при расчете промысловых газопроводов у нас и за границей получила формула Веймаута. Установлено, что формула Веймаута дает увеличенные диаметры трубы только при величине числа Рейнольдса газового потока
где D – внутренний диаметр трубы, м; р1 и p2 – абсолютные давления в начале и конце трубопровода, Па; Пример 6. Определить массовую пропускную способность газопровода диаметром D = 0,2 м и длиной L = 15000 м при следующих условиях: р1 = 784532 Па; р2 = 196133 Па; р0 == 98066,5 Па и Решение. Согласно формуле (2.82)
Иногда удобно определять объемный, а не массовый расход газа. Для получения формулы объемного расхода газа при его изотермическом движении заменим в формуле (2.73)
после чего получим
Плотность газа
где dг – плотность газа относительно воздуха; RВ – газовая постоянная, отнесенная к 1 кг воздуха, Дж/кг.0С; Т — абсолютная температура перемещения газа, в К; р0 – давление газа, в кг/м2, а объем газа
Дополнительной подстановкой значении v,
Приняв Тст = 293 К; RВ = 287 Дж/кг.0С; р2, p1 и р0 в Па; D и L – в м и
Проверка точности формулы (2.84), а, следовательно, и формулы (2.82) показала, что фактическая производительность газопровода отличается от вычисленной по формуле в пределах ± 0,5%. Исследования на действующих промысловых газопроводах подтвердили ее точность. Расхождения между фактической производительностью газопровода и вычисленной по формулам (2.79) и (2.84) лежат в пределах погрешности измерительных приборов.
Формулы (2.79) и (2.84) используются также и при расчете вакуумных промысловых газопроводов, т. е. в случаях, когда и р1 и р2 меньше 0,1 МПа или p1 > 0,1 МПа > p2. Существующие формулы так называемого "низкого давления" применимы только при движении газа по трубе, в которой изменением объема газа можно пренебречь, т. е. перепад давления (p1 – p2) не должен превышать 1470 – 1960 Па. Например, в системе труб бытового потребления газа, где p1 = 101,0 кПа, р2 = 98,6 кПа и р1/р2 = 1,025 кПа. С увеличением перепада погрешность быстро возрастает, доходя до 19% при перепаде давления 9,8 кПа. Так как перепад давлений в промысловых вакуумных системах труб сбора газа значительно выше и исчисляется преимущественно в 27,0 кПа и более (при этом происходит заметное изменение объема газа), то формулы так называемого "низкого давления" нельзя рекомендовать для гидравлического расчета вакуумных систем труб для сбора газа. Однако для гидравлического расчета системы сбора продуктов испарения из резервуаров ею можно пользоваться ввиду того, что перепад давления в них исчисляется в десятках и реже сотнях Па. Формулу низкого давления можно получить из (2.84), если в ней вместо
Из (2.84) следует, что при постоянных dг, Т и z
т. е. при движении газа длина трубы, по которой перемещается газ, пропорциональна разности квадратов давлений начального р1 и конечного р2, а не разности этих давлений, как это имеет место при движении жидкости. Далее из уравнения (2.86) следует
Из уравнения (2.87) следует, что при уменьшении длины трубы L будет изменяться только величина р2, но она будет изменяться по отношению к L так, что правая часть будет все время постоянной. Если затем на трубе длиной L выделить две точки с давлением
во второй точке
Рис.2.10.
Вычитая второе уравнение из первого, получим
Отсюда
Из сравнения полученного уравнения с уравнением (2.87) следует, что разность квадратов начального р1 и конечного давления р2, отнесенная к единице длины трубы постоянного диаметра, есть величина постоянная как для всей трубы (уравнение (2.87)), так и для части ее (уравнение (2.88)), в данном случае ограниченной длиной l. Теперь допустим, что по трубе длиной L, с давлением вначале p1 и в конце – р2, требуется перемещать переменное количество газа. Тогда для соблюдения заданных условий необходимо изменять диаметр трубы. В этом случае в уравнении (2.87) переменными будут Q и D, а постоянной величиной – произведение А2 и
Отсюда
где
Закон изменения давления газа в трубе определяется формулой (2.84). Для отрезка ab (рис.2.11) уравнение газового потока будет
для отрезка ВС
Приравнивая правые части этих уравнений и производя соответствующие преобразования, получим
где рх – давление в какой-либо точке отрезка трубы АС.
Рис.2.11.
Согласно формуле (2.91) давление газа при его движении по трубе уменьшается по параболической кривой, следовательно, гидравлический уклон при движении газа по трубе изображается параболой, а не прямой линией, как при движении жидкости. На рис. 2.12 приведен закон изменения давления газа, перемещаемого по трубе, длина которой принята за единицу. Из рис. 2.12 следует, что на начальном участке длиной, равной 0,75 от общей длины, давление снижается на такую же величину, как и на оставшейся четверти длины, т. е. давление в начале трубы падает медленнее, а чем дальше от начала, тем быстрее.
Непрерывное увеличение гидравлического уклона объясняется тем, что с уменьшением давления объем, а вместе с ним и скорость увеличиваются. Это вызывает увеличение гидравлических сопротивлений, повышающих гидравлический уклон. Следовательно, повышение начального давления газа при его перемещении по трубе выгодно. Иногда требуется знать среднее давление газа при перемещении его по трубе. Оно определяется по формуле
Из формулы (2.92) следует, что среднее давление газа больше среднеарифметического давления вследствие того, что уменьшение его происходит не по прямой, а по выпуклой кривой.
Рис.2.12. Кривая падения давления газа, движущегося в трубе
Формулу (2.89) с точностью, достаточной для промысловой практики, можно применять для гидравлического расчета движения газа по трубе длиной L с количеством его, непрерывно увеличивающимся от Q1 до Q2. При давлении в начале трубы p1, а в конце – р2, d и Т принимают в расчетах постоянными по длине трубы, поэтому получим формулу общего вида для определения диаметра трубы, соответствующего количеству проходящего по ней газа Q1, Q2, Q3 и Q4, т.е.
где n – участок, соответствующий количеству проходящего по нему газа Qn.
2.8 Предупреждение засорения нефтепроводов и методы удаления отложений Засорение выкидных линий и нефтесборных коллекторов, проложенных на территории нефтяного месторождения, происходит по следующим причинам. 1. Ввиду недостаточной скорости потока твердые частицы, выносимые из скважин вместе с нефтью на поверхность, оседают в нефтепроводе, уменьшая его проходное сечение. 2. При определенных термодинамических условиях из совместного потока нефти, газа и воды могут выпадать соли и асфальтосмолопарафиновые отложения (АСПО), создающие твердый, трудно разрушаемый осадок. 3. При интенсивной коррозии разрушаются внутренние стенки трубопроводов, аппаратов, оборудования, в результате образовавшиеся продукты коррозионных процессов при низких скоростях потока жидкости оседают в трубопроводах и уменьшают проходное сечение.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.67 (0.014 с.) |

 . (2.73)
. (2.73) . (2.74)
. (2.74) , (2.75)
, (2.75) . (2.76)
. (2.76) , (2.77)
, (2.77) – плотность газа при атмосферных условиях.
– плотность газа при атмосферных условиях.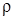 в уравнение (2.74), проинтегрируем его в пределах от р1 до р2, т. е. от начального и конечного давлений в газопроводе длиной L
в уравнение (2.74), проинтегрируем его в пределах от р1 до р2, т. е. от начального и конечного давлений в газопроводе длиной L , (2.78)
, (2.78)
 имеем
имеем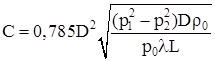 . (2.79)
. (2.79) зависит от режима движения газа. В промысловых газопроводах режим движения всегда турбулентный. Для такого режима существует несколько формул, определяющих величину
зависит от режима движения газа. В промысловых газопроводах режим движения всегда турбулентный. Для такого режима существует несколько формул, определяющих величину  . (2.80)
. (2.80) . (2.81)
. (2.81)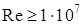 и заниженные – при
и заниженные – при  . В промысловых же газосборных системах Re находится в промежуточной зоне. Заменив в (2.79)
. В промысловых же газосборных системах Re находится в промежуточной зоне. Заменив в (2.79)  , (2.82)
, (2.82) – плотность газа в начале трубы при атмосферных условиях в кг/м3; L – длина трубы, м.
– плотность газа в начале трубы при атмосферных условиях в кг/м3; L – длина трубы, м.
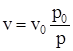 ,
, .
.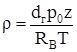
 .
.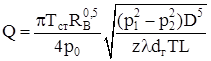 . (2.83)
. (2.83) . (2.84)
. (2.84) принять
принять  , т.е.
, т.е. . (2.85)
. (2.85) , (2.86)
, (2.86) . (2.87)
. (2.87) и
и  , из которых первая находится на расстоянии l 0, а вторая – на расстоянии l от начала трубы (рис.2.10), то согласно (2.86) давление в первой точке будет
, из которых первая находится на расстоянии l 0, а вторая – на расстоянии l от начала трубы (рис.2.10), то согласно (2.86) давление в первой точке будет ,
, .
.
 .
. . (2.88)
. (2.88) , т. е.
, т. е. .
. , (2.89)
, (2.89) . (2.90)
. (2.90) ;
; .
. , (2.91)
, (2.91)
 . (2.92)
. (2.92)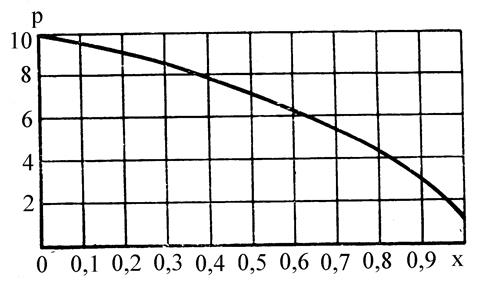
 , (2.93)
, (2.93)


