
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициентов местных гидравлических сопротивленийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ
Цель работы Закрепить экспериментом и расчетом теоретические знания по разделу «Гидравлические сопротивления».
Теоретическая часть Местными называют потери напора или давления на изменение формы или направления потока в местах резкого изменения геометрии русла. Связано это с более быстрой, чем на прямых участках, потерей устойчивости частиц жидкости, взвихриванием потока и потерей энергии частиц при их столкновении между собой и со стенками русла. Потери напора hм или давления ∆Pм определяются в практике расчетов по формуле Вейсбаха, где они поставлены в зависимость от скоростного напора или скоростного давления
hм = ξv2/2g, (1)
∆Pм = ξρv2/2g. (2) Здесь ξ - коэффициент местного сопротивления. B большинстве практических случаев Re>Rekp, т.е. поток турбулентный, и коэффициент ξ определяется из таблиц в зависимости от геометрического фактора. Критические числа Рейнольдса для местных сопротивлений весьма малы, и ламинарный режим здесь достигается при очень малых скоростях потока. В этом случае коэффициент ξ определяется с поправкой Альтшуля. В общем случае рассчитанные потери на местных сопротивлениях суммируются (принцип наложения). Однако, для близко расположенных сопротивлений (ориентировочно l ≤ (20…50)dэ ) ξ ≠ ∑ξi.В этом случае на практике приходится определять общий коэффициент опытным путем, что и является задачей настоящей лабораторной работы, хотя и для достаточно простых сопротивлений. Здесь задача обратная расчетной: определить коэффициент местного сопротивления при известном, измеренном значении потерь на этом сопротивлении hм.Формула (1) переписывается относительно ξ = Очевидно, опытом необходимо определить потери hм и скорость потока v. По условию баланса полных напоров в сечениях 1 и 2 до и после сопротивления H1=H2 + hм, откуда hм =
Содержание и порядок выполнения работы Работа выполняется с использованием стенда, схема которого представлена на рисунке 1. Здесь трубопровод смонтирован в вертикальной плоскости и включает в себя местные сопротивления: А - внезапное расширение; Б - внезапное сужение; В4 - вентиль; Г - поворот на 90°; Д - плавный поворот на 180°. Трубопровод подключен через вентиль к резервуару, обеспечивающему постоянный напор Н, и имеет выход через вентиль В5 в мерный бачек МБ, который связан со сливной линией через вентиль В12. Между местными сопротивлениями встроены пьезометрические трубки П4…П9 со стеклянными окончаниями, выведенными на панель под соответствующими номерами 4... 9. Основными задачами работы являются: 1. Определение коэффициентов местных сопротивлений А, Б, В4, Г, Д соответственно ξА, ξб, ξВ4, ξГ, ξД. 2. Построение графика зависимости местных потерь на вентиле В4 hм(В4) от расхода Q. 3. Построение линий полного и пьезометрического напоров для участка трубопровода между пьезометрами П4... П7. Для выполнения работы определяются измерениями с последующей вычислительной обработкой напоры: полные Н, геометрические zi, пьезометрические Pi/γ, скоростные αiv2i/2g. Поток считается заведомо турбулентным, что обусловливает значения коэффициентов Кориолиса αi=1. Геометрический напор zi определяется прямым измерением при помощи линейки от произвольной базы. Например, на рисунке для сечений пьезометров П4…П7 нулевой уровень будет совпадать с произвольной плоскостью отсчета. Очевидно, для сечений пьезометров П8 – П9 значение геометрического напора будет отрицательным. Значения Пi =zi + Pi/γ считается со шкал на панели, которые имеются для каждого пьезометра и проградуированы всантиметрах. Для определения скоростных напоров необходимо предварительно измерить расход Qо, для чего используется метод мерной емкости. С этой целью измеряется время заполнения мерногобачка (МБ) t, от уровня воды hδ1, - перед включением секундомера, до уровня hδ2 - окончания измерения. Рассчитывается объем бачка Vδ= b1b2 hδ, см3, (5) где b1 = b2 = 20 см - размеры сторон бачка; Dh = hδ2 - hδ1, см Тогда расход Qо во время опыта Qо = Vδ / t, см3/c. (6) Осредненная по i -му сечению скорость потока определяется из уравнения неразрывности потока vi = 4Qо / πd2i, (7) где di - диаметр проходного сечения, см. Для приведения к общеупотребительной в технической практике размерности значения напоров zi, Pi / γ и v2/2g, полученные в сантиметрах, целесообразно перевести в метры. Полные напоры для каждого i -го сечения Hi = zi +Pi/γ +αiv2i/2g (8) Потери напора на i – ом местном сопротивлении определяются по формуле hм(i) = Hi – Hi+1 (9) где порядок i сопротивления устанавливается по предшествующему пьезометру. Например, для сопротивления А hм(A) = H1 – H2 После определения потерь hм(i) вычисляются по формуле (3) значения коэффициентов местных сопротивлений ξi. Для точности опыт повторяется n раз, и в формулу (3) подставляется среднеарифметическое из j-х значений (математическое ожидание)
Для построения пьезометрической и напорной линии в сиcтеме координат Z - X изображается участок трубопровода П4…П7; для сечений П4…П7 откладывается в масштабе значения zi, Pi/γ, v2i/2g, Нi и hм(i). Пьезометрическая линия образуется соединением точек Pi/γ, линия полного напора - соединением точек Hi. Для построения графика зависимости hм(Q) для вентиля В4, принимается диапазон расходов 0.5Qо…2.5Qо и производятся вычисления потерь по формуле (1) с использованием (7). Строится график hм(Q). Последовательность проведения опыта следующая: 1. Произвести измерения геометрических параметров zi и di; 2. Убедиться в заполнении трубопроводов по наличию воды в пьезометрах (вентиль В3) и в отсутствии воды в мерном бачке МБ (вентиль В12); 3. Открыть вентиль В5 и плавными движениями отрегулировать расход до снижения уровней в пьезометрах ориентировочно до значений 0...25 см; 4.Закрыть выход из бачка вентилем В12, замерить линейкой уровень воды и включить секундомер. Два последних действия произвести одновременно; 5. Во время наполнения бачка записывать показания пьезометров П4…П9 в таблицу 1; 6. По приближении уровня воды в бачке к верхнему выпускному отверстию измерить уровень hδ2 и выключить секундомер; 7. По приведенным формулам, произвести расчеты и заполнить таблицу 1 и таблицу 2.
Таблица 1 – Результаты измерений и расчетной обработки параметров
Таблица 2 – Результаты расчета коэффициентов местных сопротивлений
Лабораторная работа № 2
СОПРОТИВЛЕНИЯ В ТРУБЕ Цель работы. Экспериментальное определение коэффициента гидравлического сопротивления по длине трубопровода и коэффициенташероховатости.
2 Содержание работы: - выявить основные факторы, влияющие на потери удельной гидравлической энергии по длине трубопровода; - установить взаимосвязь между коэффициентом гидравлического сопротивления, числом Рейнольдса, относительной шероховатостью и диаметром трубопровода; - определить потери удельной гидравлической энергии приламинарном и турбулентном режимах движения жидкости в трубопроводах; - ознакомиться с методикой экспериментального определениякоэффициента гидравлического сопротивления по длине трубопровода и коэффициента шероховатости.
3 Порядок выполнения работы: - изучить содержание методического указания и теоретический материал, связанные с данной работой; - ответить на контрольные вопросы; - ознакомиться с испытательным стендом и порядком проведения лабораторной работы; - провести эксперименты; - обработать результаты исследований и представить в видеграфиков или таблиц; - оформить и защитить отчет по лабораторной работе.
4 Оборудование для работы: Лабораторный испытательный стенд и методические указания.
Теоретическая часть Потери на трение или потери по длине – это потери энергии, которые возни кают в прямых трубах постоянного сечения при равномерном течении и возрастают пропорционально длине трубы (рисунок 1). Этот вид потерь обусловлен внутренним трением в жидкости, трением о стенки, и поэтому имеет место не только в шероховатых, но и гладких трубопроводах. Потери напора по длине трубопровода, как показали опыты, зависят от средней скорости движения жидкости v, линейного размера живого сечения (диаметр, гидравлический радиус и др.), вязкости μ, плотности ρ, шероховатости стенок, выраженной средним размером выступов ∆ и длины трубопровода l. Функционально это зависимость имеет вид hтр = f(v, d, μ, ρ, ∆, l) Потерю напора можно выразить по общей формуле для гидравлических потерь hтр = ξтрv2/2g, (1) Однако удобнее коэффициент ξтр связать с относительной длиной трубы l /d. Возьмем участок круглой трубы длиной, равной ее диаметру и обозначим коэффициент его сопротивления, входящий в формулу (1), через λ. Тогда по всей трубе длиной l и диаметром d (рисунок 1) коэффициент сопротивления будет в l /d раз больше
Рисунок 1 – Участок круглой трубы
В результате формула (1) примет вид
или в единицах давления
где γ – удельный вес жидкости. Зависимость (2) называется формулой Дарси. Безразмерный коэффициент λ называется коэффициентом потерь на трение или коэффициентом сопротивления трения. Его можно рассматривать как коэффициент пропорциональности между потерей напора на трение с одной стороны, и произведением относительной длины трубы на скоростной напор с другой стороны. Для трубопроводов, имеющих свободную поверхность, что соответствует безнапорному потоку, коэффициент трения равен
где RГ – гидравлический радиус. Для круглого трубопровода RГ = d / 4. Обозначая
где С – коэффициент Шези, характеризующий шероховатость стенок трубопровода. Решая уравнение (5) относительно скорости и вводя обозначение i = hтр / l (гидравлический уклон) получим
Гидравлический уклон показывает потери энергии на единице длины трубопровода. Поверхности стенок труб (каналов) имеют ту или иную шероховатость. Обозначим высоту выступов шероховатости буквой ∆. Обычно ∆ называют абсолютной шероховатостью, а ее отношение к радиусу трубы (∆/r = 2∆/d) – относительной шероховатостью. Величина, обратная шероховатости называется относительной гладкостью (r/∆). С целью упрощения расчетов вводят понятие эквивалентной шероховатости kэ, при которой потери напора в трубопроводе получаются такими же, как и при фактической неоднородной шероховатости.
Таблица 1 - Значение kэ для трубопроводов различного назначения
В зависимости от соотношения толщины ламинарного слоя δ и абсолютной шероховатости ∆ различают гидравлически гладкие и шероховатые трубопроводы. Если ламинарный слой полностью закрывает выступы и неровности на стенках трубы (δ>∆), трубопровод считается гидравлически гладким. Если же δ<∆, то трубопровод считается гидравлически шероховатым. В общем случае коэффициент λ является функцией λ = f(Rе; kэ /d) числа Рейнольдса и относительной шероховатости. Существуют следующие зависимости для определения коэффициента трения λ:
а) Rе<10
б) 10
в) Rе > 500
Коэффициент шероховатости определяется из формулы Махлинча
откуда
РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ
1 Цель работы: Экспериментальное определение числа Рейнольдса для различных режимов течения жидкости в трубопроводе круглого сечения.
Содержание работы - проследить наличие разных режимов течения жидкости в трубопроводе круглого сечения; - установить для каждого режима течения число Рейнольдса; - выявить переход от ламинарного режима течения к турбулентному и найти критическое значение числа Рейнольдса; - уяснить физический смысл существования верхней и нижней критических скоростей движения жидкости; - ознакомиться с методикой экспериментального определения числа Рейнольдса.
Порядок выполнения работы - изучить содержание методического указания и теоретический материал; - ответить на контрольные вопросы; - ознакомиться с испытательным стендом и порядком проведения лабораторной работы; - провести эксперименты; - обработать результаты исследований и представить в виде графиков или таблиц; - оформить и защитить отчет по лабораторной работе.
Оборудование для работы лабораторный испытательный стенд и методическое указание.
Теоретическая часть В инженерной практике часто требуется знать величину потерь энергии при движении жидкости в трубопроводах. Потери энергии зависят от режима движения жидкости. Следовательно, для того, чтобы определить потери энергии на преодоление сопротивления по длине трубопровода или в местных участках необходимо прежде всего установить режим движения. Возможны два установившихся режима течения жидкостей и газов в трубах: - ламинарный, - турбулентный. Между двумя установившимися режимами движения существует третий, получивший название переходного. Ламинарное течение – это слоистое течение без перемешивания частиц жидкости и без пульсации скорости. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, отсутствуют поперечные перемещения жидкости. Таким образом, ламинарный режим является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и не установившимся). Турбулентное течение – это течение, сопровождающееся интенсивным перемещением жидкости, пульсацией скоростей и давлений. Движение отдельных частиц носит хаотичный характер, траектории под час имеют вид замысловатых кривых. Объясняется это тем, что при турбулентном течении, наряду с основными продольными перемещениями частиц жидкости вдоль трубопровода, имеют место поперечное и вращательное движение отдельных объемов. Режим движения жидкости зависит от величины средней скорости течения v ср,от характерного линейного размера (для круглой трубы этим размером является диаметр d) и от коэффициента кинематической вязкости n, определяемого температурой жидкости t°C. Смена режима течения жидкости в трубопроводе происходит при определенной скорости течения v кр, которую называют критической. Как показали многочисленные эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости n и обратно пропорционально диаметру d трубы
Входящий в формулу коэффициент пропорциональности k имеет универсальное значение и одинаков для любых диаметров труб. Это значит, что смена течения происходит при вполне определенном соотношении между скоростью, диаметром и вязкостью n, равном:
Критических скоростей две: 1) верхняя критическая скоростьv кр.в, когда режим ламинарный сменяется турбулентным; 2) нижняя критическая скорость vкр.н, когда турбулентный режим переходит в ламинарный. Указанное положение наглядно иллюстрируется диаграммой. На диаграмме выделено три области: 1. Область устойчивого ламинарного режима. 2. Область устойчивого турбулентного режима. 3. Переходная область, в которой могут иметь место и ламинарный и турбулентный режимы в зависимости от величины скорости.
Если скорость изменяется в сторону увеличения, то в переходной области преобладает турбулентный режим, если в сторону уменьшения – ламинарный. Оба режима в переходной области неустойчивы, они нарушаются под действием самых незначительных причин. Особенно неустойчивым является ламинарный режим. Поэтому в практике принимают для переходной области режим турбулентный, а за критическую скорость – нижнее ее значение. Английский физик О. Рейнольдс своими опытами в 1883 г. доказал теоретическое предположение Д.И. Менделеева о существовании ламинарного и турбулентного режимов и установил их зависимость от соотношения определенных физических величин. Указанное отношение было названо числом Рейнольдса, которое для круглых трубопроводов определяется по формуле:
Переход от одного режима движения к другому происходит при критическом числе Рейнольдса, величина которого равна:
Критическое число Рейнольдса для труб круглого сечения приблизительно равно: Reкр=2320. Таким образом, получен критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях Re<Reкр течение оказывается ламинарным; при Re>Reкр происходит переход к турбулентному режиму. Многочисленными наблюдениями за движением жидкости в круглой трубе установлено, что если число Рейнольдса меньше значения Re=2320, то режим будет устойчивым ламинарным, а если число больше Re = 4000, то режим устойчиво турбулентный. В переходной области за критическое принимается число Рейнольдса, соответствующее нижнему значению критической скорости: а) при движении жидкости в круглой трубе Reкр=2320; б) при движении в любом русле можно принимать Reкр=580. На практике имеют место как ламинарное, так и турбулентное течение, причем первое течение наблюдается тогда, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно имеет место в трубопроводах, по которым движутся бензин, керосин, спирты, кислоты и другие маловязкие жидкости. Из величин, входящих в формулу (3) неизвестными величинами являются v ср. и n, которое можно определить, измерив расход и температуру жидкости.
Содержание работы - установить взаимосвязь между основными параметрами (давление, скорость) потока движущейся жидкости; - изучить геометрический и энергетический смысл уравнения Бернулли для элементарной струйки идеальной и реальной жидкости; - разобрать графическую иллюстрацию уравнения Бернулли для реального потока; -ознакомиться с методикой экспериментального определения параметров движущейся жидкости.
Порядок выполнения работы - изучить содержание методического указания и теоретический материал, связанные с данной работой; - ответить на контрольные вопросы; - ознакомиться со стендом и порядком проведения лабораторной работы; - провести эксперименты; - обработать результаты исследований и представить в виде графиков и таблиц; - оформить и защитить отчет по данной работе.
4 Оборудование для работы Лабораторный стенд и методические указания.
5 Теоретическая часть 5.1 Уравнение Бернулли для элементарной струйки идеальной жидкости Уравнение Бернулли, устанавливающее связь между давлением и скоростью в движущемся потоке жидкости, является основным уравнением гидравлики. Написанное для двух произвольных сечений элементарной струйки идеальной жидкости уравнение Бернулли имеет вид:
Координата z [м], определяет высоту положения частицы над какой-то плоскостью сравнения, называемой нивелирной высотой, или геометрическим напором, и определяет запас потенциальной энергии, обусловленный положением частицы (удельная потенциальная энергия положения). Величина Суммой этих двух величин z + P/γ, называемой статической высотой или статическим напором, определяется полный запас потенциальной энергии 1 Н жидкости относительно принятой плоскости сравнения. Величина v2/2g [м] представляет собой высоту столба жидкости, эквивалентную часть статического напора, под действием которого происходит движение жидкости. Эта величина, называемая динамическим, или скоростным напором, представляет собой удельную кинетическую энергию, т.е. кинетическую энергию, отнесенную к 1Н жидкости:
Уравнение Бернулли показывает, что при установившемся движении идеальной жидкости сумма геометрического, пьезометрического и динамического напоров в каждом поперечном сечении элементарной струйки есть величина постоянная, т.е.
Физический смысл этого уравнения заключается в том, что суммарная (полная) удельная энергия элементарной струйки идеальной жидкости при установившемся движении, состоящая из удельной потенциальной и удельной кинетической энергии, остается неизменной.
5.2 Уравнение Бернулли для элементарной струйки реальной жидкости При движении реальной жидкости часть энергии будет теряться на преодоление гидравлических сопротивлений и запас энергии Е во всяком последовательном поперечном сечении струйки будет меньше, чем в предыдущем. Таким образом, для каждой элементарной струйки реальной жидкости можно написать: Е1=Е2+Нпот или то же самое в развернутом виде:
где Нпот – дополнительный член в уравнении Бернулли, учитывающий потерю напора на участке между сечениями 1-1 и 2-2. Благодаря линейной размерности всех членов уравнения Бернулли связь между напорами (z, Р/g, v2/2g) наглядно изображается графически (рисунок 1).
Линия АА, характеризующая падение удельной энергии жидкости, называется линией энергии или напорной линией. Отношение абсолютной величины потери напора Нпот к длине l, на которой она происходит, называется гидравлическим уклоном i, т.е. i = Hпот / l. Линия ББ, характеризующая изменение давления по длине струйки, называется пьезометрической линией. Положение оси элементарной струйки характеризует изменение геометрического напора вдоль длины трубки тока. Плоскость 00, от которой производится отсчет геометрических высот, называется плоскостью сравнения.
5.3 Уравнение Бернулли для потока жидкости Чтобы практически использовать уравнение Бернулли, полученное для элементарной струйки, необходимо распространить его на целый поток, являющийся совокупностью элементарных струек, движущихся с различными скоростями. При введении в уравнение Бернулли средней скорости потока vср необходимо ввести в него поправочный коэффициент a, так как кинетическая энергия потока, вычисленная по средней скорости, будет отличаться от истинной кинетической энергии потока. Таким образом, уравнение Бернулли, написанное для установившегося потока реальной жидкости, имеет следующий вид:
Коэффициент Кориолиса a характеризует неравномерность распределения скоростей в поперечном сечении потока и представляет собой отношение истинной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости:
где S - площадь живого сечения потока. С помощью уравнения Бернулли решается большое количество задач, связанных с движением жидкости. При решении этих задач подбирается два сечения потока так, чтобы для одного из них были известны величины z, P, v, а для другого – одна или две из них подлежали определению.
При двух неизвестных величинах, помимо уравнения Бернулли, используют уравнение расхода и решают полученную систему уравнений совместно.
6 Описание лабораторного испытательного стенда Испытательный стенд для демонстрации уравнения Бернулли (рисунок 2) состоит из трубопровода, на котором выделены характерные сечения 1, 2, 3. В соответствующих местах установлены пьезометры 1, 2, и 3 для измерения пьезометрического напора Р/g. Подача жидкости осуществляется открытием вентиля В1. Отвод (слив) жидкости производится по трубопроводу через вентиль В2 в мерный бачок МБ. Вентиль В12 служит для выпуска жидкости из мерного бачка в сливной трубопровод. Расход жидкости через сечения 1, 2, 3 замеряется объемным способом. Регулирование скорости движения в трубопроводе осуществляется вентилем В2.
7 Порядок проведения опытов и обработки экспериментальных данных После ознакомления с испытательным стендом опыты проводятся в следующем порядке: 1. Закрыть вентиль В2 и, открыв вентиль В12, выпустить жидкость из мерного бачка. Убедившись, что в мерном бачке жидкости нет, вентиль В12 закрыть. 2. Открыть вентиль В1 и заполнить установку жидкостью. После заполнения уровень жидкости в пьезометрах должен быть одинаков. 3. Плавным открытием вентиля В2 добиваются установившегося движения жидкости в трубопроводе (уровень в пьезометрах П1, П2, П3 должен занять определенное положение). Одновременно, с момента открывания вентиля В2, засекают время наполнения мерного бачка до отметки, указанной на нем. 4. Во время наполнения мерного бачка снимают показания с пьезометров П1, П2, П3 и заносят их в таблицу 4.1.
Рисунок 2 – Схема лабораторного стенда
После наполнения мерного бачка вентиль В2 закрыть. Время заполнения бачка рабочей жидкостью до указанной отметки записывается в таблицу 1. 5. Открыть вентиль В12 и выпустить жидкость из мерного бачка МБ. 6. На опытной установке замерить расстояние z1, z2, z3, а также расстояние l1 и l2 между пьезометрами на установке. На основе данных наблюдений и замеров определяют: а) расход в трубопроводе Q по формуле
где W – объем мерного бачка (0,2*,0,2*0,24м3), t – время наполнения мерного бачка; б) среднее расстояние скорости в сечениях по формуле
где Q – расход жидкости в трубопроводе, S1, S2 и т.д. – площади живых сечений, где установлены пьезометры; в) скоростной напор v2/2g определяют по средней скорости в тех же сечениях; например, для сечения 1 будет v12 /2g. г) полный напор д) потери на участке и в целом по трубе, как разность полных напоров на участке и в целом по трубе, (принимая a1 = a2 = 1)
е) гидравлический уклон на каждом участке или трубы в целом
где l1 – расстояние между 1 и 2 сечениями; l2 – расстояние между 2 и 3 сечениями. По результатам измерений и вычислений выполняют построение пьезометрической линии (z1+P1/γ; z2+P2/γ; z3+P3/γ) и линии полного напора
Таблица 1 -Данные измерений и вычислений
8 Содержание отчета - цель и содержание работы; - схема испытательного стенда; - порядок проведения опытов и обработки экспериментальных данных (включая журнал измерений и вычислений); - краткие выводы;
9 Контрольные вопросы 1. Вывод уравнения Бернулли для элементарной струйки идеальной жидкости? 2. Уравнение Бернулли для потока вязкой жидкости, его отличие от уравнения для идеальной несжимаемой жидкости? 3. Что учитывает коэффициент Кориолиса в уравнении Бернулли? 4. Физический смысл геометрического и пьезометрического уклонов, в чем их различие? 5. В чем заключается геометрический и энергетически смысл уравнения Бернулли? 6. Как определяется пьезометрический напор в заданном сечении трубопровода? 7. Объясните порядок построения линии полного напора?
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАСХОДА РАСХОДОМЕРА ВЕНТУРИ
1 Цель работы: Определить расход жидкости в трубопроводе, используя расходомер Вентури.
2 Содержание работы: - изучить примеры использования уравнения Бернулли при решении гидравлических задач и в технике; - установить взаимосвязь между скоростью жидкости и рабочим давлением при ее движении в трубопроводе переменного сечения; - ознакомиться с методикой теоретического и экспериментального определения расхода жидкости в трубопроводе.
3 Порядок выполнения работы: - изучить содержание методического указания и теоретический материал, связанных с данной работой; - ответить на контрольные вопросы; - ознакомиться с испытательным стендом и порядком проведения лабораторной работы; - провести эксперименты; - обработать результаты исследований и представить в виде таблиц; - оформить и защитить отчет по лабораторной работе.
Оборудование для работы Лабор
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 865; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.013 с.) |

 . (3)
. (3) . (4)
. (4) . (10)
. (10)
 .
.
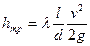 (2)
(2) , (3)
, (3) , (4)
, (4) , получим несколько видоизмененную формулу
, получим несколько видоизмененную формулу , (5)
, (5) . (6)
. (6) - гидравлически гладкие трубопроводы;
- гидравлически гладкие трубопроводы; (формула Блазиуса) (7)
(формула Блазиуса) (7) (формула А.Д. Альтшуля) (8)
(формула А.Д. Альтшуля) (8) (формула Шифринсона) (9)
(формула Шифринсона) (9) ,
, .
. . (1)
. (1) . (2)
. (2) . (3)
. (3) . (4)
. (4) . (1)
. (1)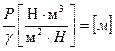 , представляющая высоту столба жидкости, уравновешивающего действующее в данной точке давление, называется пьезометрической высотой или пьезометрическим напором, и определяет запас потенциальной энергии, обусловленной давлением (удельная потенциальная энергия давления).
, представляющая высоту столба жидкости, уравновешивающего действующее в данной точке давление, называется пьезометрической высотой или пьезометрическим напором, и определяет запас потенциальной энергии, обусловленной давлением (удельная потенциальная энергия давления).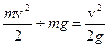 .
.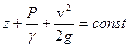 .
. , (2)
, (2)
 . (3)
. (3) ,
,
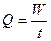
 и т.д.
и т.д.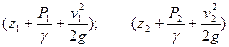 и т.д.
и т.д. и т.д.
и т.д.
 .
.


