
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок проведения опытов и обработки экспериментальных данныхСодержание книги
Поиск на нашем сайте
После ознакомления с испытательным стендом опыты проводятся в следующем порядке: 1. Закрыть вентили В8, В9, В10, В11. Открыть вентиль В12 и выпустить жидкость из мерного бачка, после чего вентиль В12 закрыть. 2. Открыть вентиль В8 и заполнить трубопровод рабочей жидкостью. Уровень жидкости в пьезометрах П11 и П10 должен быть одинаковым. 3. Плавно открывая вентиль В9, одновременно засечь время наполнения мерного бачка МБ до отметки, указанной на бачке. Установить режим движения, при котором уровень жидкости в пьезометре 11 займет одно из промежуточных значений в диапазоне (20…30)10-2 м. 4. Снять показания с пьезометров П11 и П10, которые соответствуют значениям (z11 + P11/γ) и (z10 + P10/γ). Результаты измерения занести в журнал наблюдений. 5. После того, как уровень жидкости в мерном бачке достигнет отметки «с», вентиль В9 закрыть и одновременно засечь время наполнения. Результаты измерения занести в журнал наблюдений. 6. Открыть вентиль В12 и выпустить жидкость из мерного бачка, после чего вентиль В12 закрыть. 7. Со стенда снять значения d2 и L2. 8. Закрыть вентиль В8 и открыть вентиль В10. Уровень жидкости в пьезометрах П16 и П15 должен быть одинаковым. Далее в описанном порядке (начиная с п.3) повторить опыт, снимая показания с пьезометров П16 и П15, которые определяют потери в трубопроводе длиной L1 и d1. Результаты занести в таблицу 2. Уровень жидкости в пьезометре П16 установить (25…35)*10-2м.
На основе данных наблюдений и замеров определяют: а) расход жидкости в трубопроводе
где W – объем мерного бачка (0, 2 * 0,2 * 0,24) м3; t – время наполнения мерного бачка; б) среднюю скорость движения жидкости в трубопроводе где S – площадь живого сечения, S = в) гидравлический радиус Rг = d/4; г) потери по длине трубопровода
г) гидравлический уклон i =hтр/L, где L – длина трубопровода или расстояние между пьезометрами; е) коэффициент гидравлического трения
и) число Рейнольдса
υ - коэффициент кинематической вязкости, выбирается по таблице в зависимости от температуры жидкости;
к) в зависимости от численного значения Rе устанавливают режим движения жидкости в трубопроводе, а затем в соответствии с режимом по формулам (7), (8) или (9) определяют расчетное значение коэффициента трения λр
л) оценить погрешность в определении коэффициента гидравлического трения экспериментальным и расчетным путями.
Таблица 2 - Данные измерений и вычислений
8 Содержание отчета: - цель и содержание работы; - схема испытательного стенда; - порядок проведения опытов и обработки экспериментальных данных (включая журнал измерений и вычислений); - краткие выводы.
9 Контрольные вопросы 1. Чем обусловлены потери энергии при движении жидкости в прямых трубах постоянного диаметра? 2. Какие показатели влияют на коэффициент гидравлического сопротивления по длине трубопровода? 3. Как определить коэффициент гидравлического сопротивления при ламинарном режиме движения? 4. Как определяется коэффициент гидравлического сопротивления при турбулентном режиме движения? 5. Что характеризует коэффициент Шези? 6. Какие факторы влияют на коэффициент гидравлического сопротивления по длине при турбулентном режиме движения? 7. Объясните порядок проведения опыта и поставленной задачи?
Лабораторная работа № 3
РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ
1 Цель работы: Экспериментальное определение числа Рейнольдса для различных режимов течения жидкости в трубопроводе круглого сечения.
Содержание работы - проследить наличие разных режимов течения жидкости в трубопроводе круглого сечения; - установить для каждого режима течения число Рейнольдса; - выявить переход от ламинарного режима течения к турбулентному и найти критическое значение числа Рейнольдса; - уяснить физический смысл существования верхней и нижней критических скоростей движения жидкости; - ознакомиться с методикой экспериментального определения числа Рейнольдса.
Порядок выполнения работы - изучить содержание методического указания и теоретический материал; - ответить на контрольные вопросы; - ознакомиться с испытательным стендом и порядком проведения лабораторной работы; - провести эксперименты; - обработать результаты исследований и представить в виде графиков или таблиц; - оформить и защитить отчет по лабораторной работе.
Оборудование для работы лабораторный испытательный стенд и методическое указание.
Теоретическая часть В инженерной практике часто требуется знать величину потерь энергии при движении жидкости в трубопроводах. Потери энергии зависят от режима движения жидкости. Следовательно, для того, чтобы определить потери энергии на преодоление сопротивления по длине трубопровода или в местных участках необходимо прежде всего установить режим движения. Возможны два установившихся режима течения жидкостей и газов в трубах: - ламинарный, - турбулентный. Между двумя установившимися режимами движения существует третий, получивший название переходного. Ламинарное течение – это слоистое течение без перемешивания частиц жидкости и без пульсации скорости. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, отсутствуют поперечные перемещения жидкости. Таким образом, ламинарный режим является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и не установившимся). Турбулентное течение – это течение, сопровождающееся интенсивным перемещением жидкости, пульсацией скоростей и давлений. Движение отдельных частиц носит хаотичный характер, траектории под час имеют вид замысловатых кривых. Объясняется это тем, что при турбулентном течении, наряду с основными продольными перемещениями частиц жидкости вдоль трубопровода, имеют место поперечное и вращательное движение отдельных объемов. Режим движения жидкости зависит от величины средней скорости течения v ср,от характерного линейного размера (для круглой трубы этим размером является диаметр d) и от коэффициента кинематической вязкости n, определяемого температурой жидкости t°C. Смена режима течения жидкости в трубопроводе происходит при определенной скорости течения v кр, которую называют критической. Как показали многочисленные эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости n и обратно пропорционально диаметру d трубы
Входящий в формулу коэффициент пропорциональности k имеет универсальное значение и одинаков для любых диаметров труб. Это значит, что смена течения происходит при вполне определенном соотношении между скоростью, диаметром и вязкостью n, равном:
Критических скоростей две: 1) верхняя критическая скоростьv кр.в, когда режим ламинарный сменяется турбулентным; 2) нижняя критическая скорость vкр.н, когда турбулентный режим переходит в ламинарный. Указанное положение наглядно иллюстрируется диаграммой. На диаграмме выделено три области: 1. Область устойчивого ламинарного режима. 2. Область устойчивого турбулентного режима. 3. Переходная область, в которой могут иметь место и ламинарный и турбулентный режимы в зависимости от величины скорости.
Если скорость изменяется в сторону увеличения, то в переходной области преобладает турбулентный режим, если в сторону уменьшения – ламинарный. Оба режима в переходной области неустойчивы, они нарушаются под действием самых незначительных причин. Особенно неустойчивым является ламинарный режим. Поэтому в практике принимают для переходной области режим турбулентный, а за критическую скорость – нижнее ее значение. Английский физик О. Рейнольдс своими опытами в 1883 г. доказал теоретическое предположение Д.И. Менделеева о существовании ламинарного и турбулентного режимов и установил их зависимость от соотношения определенных физических величин. Указанное отношение было названо числом Рейнольдса, которое для круглых трубопроводов определяется по формуле:
Переход от одного режима движения к другому происходит при критическом числе Рейнольдса, величина которого равна:
Критическое число Рейнольдса для труб круглого сечения приблизительно равно: Reкр=2320. Таким образом, получен критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях Re<Reкр течение оказывается ламинарным; при Re>Reкр происходит переход к турбулентному режиму. Многочисленными наблюдениями за движением жидкости в круглой трубе установлено, что если число Рейнольдса меньше значения Re=2320, то режим будет устойчивым ламинарным, а если число больше Re = 4000, то режим устойчиво турбулентный. В переходной области за критическое принимается число Рейнольдса, соответствующее нижнему значению критической скорости:
а) при движении жидкости в круглой трубе Reкр=2320; б) при движении в любом русле можно принимать Reкр=580. На практике имеют место как ламинарное, так и турбулентное течение, причем первое течение наблюдается тогда, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно имеет место в трубопроводах, по которым движутся бензин, керосин, спирты, кислоты и другие маловязкие жидкости. Из величин, входящих в формулу (3) неизвестными величинами являются v ср. и n, которое можно определить, измерив расход и температуру жидкости.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.253.150 (0.009 с.) |



 и скорость напора v2/2g;
и скорость напора v2/2g;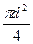 ;
;
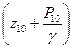 ;
;
 ;
; ;
; ,
, . (1)
. (1) . (2)
. (2) . (3)
. (3) . (4)
. (4)


