
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение через малое отверстие в тонкой стенкеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Малым называют отверстие, у которого вертикальные размеры меньше 0,1Н. В этом случае можно принять, что все точки отверстия имеют одинаковую глубину погружения, и следовательно, одинаковую скорость. Термин "тонкая стенка" не отражает геометрической толщины стенки, а указывает только, что толщина стенки не влияет на форму вытекающей струи. Этот случай движения жидкости характерен тем, что в процессе истечения потенциальной энергии, которым обладает жидкость в резервуаре, превращается с большими или небольшими потерями в кинетическую энергию свободной струи или капель. При истечении из отверстия траектории частиц в самом отверстии не будут параллельны друг другу. Параллельность будет только на некотором расстоянии от отверстия, где одновременно имеет место некоторое сжатие струи. Выходя из отверстия, струя жидкости резко сжимается, что объясняется операцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям. В струе их круглого отверстия силы инерции и силы поверхностного натяжения уравновешены по периметру ввиду их несимметричного расположения и струя в сжатом сечении имеет также форму круга. При истечении из отверстий другой формы - квадратного, прямоугольного, треугольного и др.- силы инерции и поверхностного натяжения не уравновешены по периметру, что вызывает сужение формы поперечного сечения по длине струи. Это явление называется инверсией струи. Степень сжатия струи, вытекающей через круглое отверстие, характеризуется коэффициентом сжатия. ε = Sсж / S, (1) где Sсж - площадь сжатого сечения (по расстоянию от стенки); S - площадь отверстия. Характер и величина сжатия зависят от формы и размеров отверстия и расстояния его от стенок и дна. Если боковые стенки и дно не влияют на вытекание жидкости из отверстия (что имеет место при расстоянии стенки и дна от контуров отверстия не менее трех кратных размеров отверстия в данном направлении), то такое сжатие называется совершенным. По характеру сжатие бывает полным, если струя получает сжатие по всему периметру отверстия, и неполным, если струя не имеет бокового сжатия содной или нескольких сторон, например, когда отверстие примыкает к стенке или ко дну сосуда, которые при этом являются как бы направляющими для вытекающей струи. Для малого круглого отверстия в тонкой стенке коэффициент при совершенном сжатии ε = 0,62…0,64 Большие значения соответствуют меньшим напорам и меньшим размерам отверстия. Скорость в сжатом сечении находят по уравнению Бернулли для свободного уровня жидкости в сосуде и плоскости сжатого сечения
где φ – коэффициент скорости, равный
В случае истечения идеальной жидкости ξ = 0, а, следовательно, φ = 1 и теоретическая скорость истечения
Из вышеприведенных уравнений можно заключить, что коэффициент скорости φ есть отношение действительной скорости к теоретической:
ξ – коэффициет местного сопротивления; g – ускорение силы тяжести; Н – напор истечения. Действительная скорость истечения vc всегда несколько меньше теоретической вследствие сопротивления, следовательно, коэффициент скорости всегда меньше единицы. Подсчитаем расход жидкости как произведение действительной скорости истечения на фактическую площадь сечения струи, получим Q = Sсжv, зная, что Sсж = S×ε - уравнение примет вид
Произведение коэффициента ε и φ принято обозначать буквой μ и называть коэффициентом расхода, то есть μ = ε × φ, (5) тогда формулу для определения расхода окончательно можно записать
или
где P – расчетное давление под действием, которого происходит истечение. Полученные выражения являются основными для данного раздела, так как с их помощью решается основная задача – определение расхода. Из уравнений следует, что коэффициент расхода μ равен
Это значит, что коэффициент расхода есть отношение действительного расхода к теоретическому, т.е. к тому расходу Qm, который имел бы место при отсутствии сжатия струи и сопротивления. Действительный расход всегда меньше теоретического и, следовательно, коэффициент расхода всегда меньше единицы вследствие влияния двух факторов: сжатия струи и сопротивления. В одних случаях больше влияет первый фактор, в других - второй. Как показали опыты, коэффициент расхода μ для малых отверстий равен μ = 0,6 - 0,62. При этом меньшим размерам отверстия и меньшим напорам соответствуют большие значения μ. Введенные в рассмотрение коэффициенты сжатия ε, сопротивления ξ, скорости φ и расхода μ, зависят в первую очередь от типа отверстия, а также, как и все безразмерные коэффициенты в гидравлике, от основного критерия гидродинамического подобия Rе (числа Рейнольдса). Коэффициент скорости φ для круглого отверстия обычно принимают равным φ =0,97 - 0,98 (при ξ = 0,065). При истечении маловязкой жидкости (вода, бензин, керосин и др.) через круглое отверстие в круглой стенке имеет место значительное сжатие струи и весьма небольшое сопротивление. Поэтому коэффициент расхода μ получается здесь значительно меньше единицы, главным образом засчет влияния струи.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.138.129 (0.007 с.) |

 , (2)
, (2)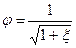 .
. .
. , (3)
, (3)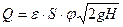 . (4)
. (4)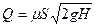
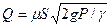 , (6)
, (6) .
.


