
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение жидкости через насадки (патрубки) при постоянном напореСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Насадком (или насадкой, или патрубком) называется весьма короткая напорная (на всем своем протяжении) труба, при гидравлическом расчете которой следует пренебрегать потерями напора по длине hl, необходимо учитывать только местные потери напора hj. Рассмотрим три случая: 1. Струя не касается стенок, а только кромок самого отверстия. В этих условиях насадок работает как отверстие. Расчет ведется по формулам, показанным раньше для отверстий (43÷47), (50), (51).
l < (2÷3) d (62)
Рис. 28. Отверстие
2. Струя сначала сужается, затем заполняет все отверстие. В этом случае это насадок. При расчете учитываются только местные сопротивления.
l= (3÷5) d (63)
Рис. 29. Насадок
3. Длина трубки больше, чем в предыдущем случае. Струя ведет себя как показано на рис. 30. В данной ситуации насадок работает как короткая труба. При расчете учитываются и местное сопротивление, и сопротивление по длине. Чем длиннее труба, тем меньше коэффициент скорости φ и коэффициент расхода
l > 5 d (64)
Рис. 30. Короткая труба
Если взять трубу и насадок одного диаметра, то увидим, что из насадка вытекает больше воды, то есть при d нас = d тр Q нас >Q тр. Наибольшее распространение получили насадки, истечение жидкости через которые рассмотрим ниже. Скорость истечения и расход жидкости через насадки определяются по тем же формулам, что и при истечении жидкости через отверстия в тонкой стенке, но с другими коэффициентами скорости φ и расхода μ. Каждый тип насадков характеризуется своими значениями коэффициентов скорости и расхода. При этом следует иметь в виду, что коэффициенты будут даваться к выходному сечению насадков. Внешний цилиндрический насадок – насадок Вентури
Рис. 31. Внешний цилиндрический насадок
При входе в насадок происходит сжатие струи, затем струя расширяется и к выходу из насадка поток заполняет полностью все сечение. Сжатие струи в насадке способствует в этой зоне образованию области с пониженным по сравнению с атмосферным давлением – вакуума. Максимальный вакуум возникает в сечении, где струя имеет наибольшее сжатие. Если в этой области подсоединить жидкостный вакуумметр, то он поднимается на вакуумметрическую высоту [7] h вак = (0,75÷0,8) Н. (65)
Наличие вакуума вызывает подсос жидкости, вследствие чего увеличивается коэффициент расхода и сам расход. Так как при выходе из насадка сжатие струи отсутствует, то коэффициент сжатия ε =1. Другие коэффициенты: μ=φ =0,82, ζ =0,5. Легко подсчитать, если к отверстию (μ =0,62) присоединить цилиндрический насадок (μ =0,82), то расход увеличится на 33%. Величину вакуума также можно рассчитать с помощью уравнения Бернулли. Выбрав сечение 1-1 в сжатом сечении струи (в уравнении (66) индекс «с»), 2-2 на выходе струи из насадка, ось 0-0 вдоль оси насадка, можно получить следующее уравнение (
Потеря напора будет определяться как местная потеря на внезапное расширение струи по формуле:
Если истечение происходит в атмосферу, то р2=рат. Тогда (66) перепишется:
На основании уравнения неразрывности (4) выразим скорость в сжатом сечении:
Используя зависимость (38), можно выражение (66) переписать
Коэффициент внутреннего сжатия в цилиндрическом насадке равен [6] ε = 0,64. Уравнение (65) после подстановок и несложных преобразований примет вид:
Если давление на свободной поверхности резервуара атмосферное и истечение происходит в атмосферу, скорость истечения из насадка определится по формуле (43) для малых отверстий в тонкой стенке. Подставляя выражение (43) в (72), получим:
Так как абсолютное давление рс не может быть меньше упругости насыщенных паров жидкости руп, предельный напор, при котором может происходить истечение жидкости в атмосферу, на основании выражения (73) определится
Так как для воды [6] при температуре Т= +20°С упругость насыщенных паров руп =0,238 м вод. ст. = 2332,4 Па. Атмосферное давление рат = 760 мм рт. ст. = 10,33 м вод. ст. = 101234 Па, то можно подсчитать предельный напор, при котором может работать насадок при истечении жидкости в атмосферу:
При больших напорах происходит срыв вакуума, и насадок перестает работать полным сечением. Струя в этом случае или проскакивает через насадок, не касаясь стенок, или прилипает к одной стороне, рис. 32.
Рис. 32. Срыв вакуума насадка
При истечении под уровень истечение неполным сечением невозможно. Однако если абсолютное давление в сжатом сечении достигнет значения, равного упругости насыщенных паров этой жидкости при данной температуре, то в насадке начинается местное закипание жидкости с последующей конденсацией паров в области повышенного давления. Это явление называется кавитацией. При возникновении кавитации значительно возрастают сопротивления, и коэффициент расхода уменьшается. Внешние цилиндрические насадки используются для уменьшения времени истечения жидкости из резервуаров (по сравнению с отверстием). Они широко применяются на практике. Как насадки такого типа работают водовыпуски в плотинах, трубы под насыпями и т.д. Такие внешние насадки не всегда удобны. Поэтому иногда делают внутренние цилиндрические насадки. Внутренний цилиндрический насадок – насадок Бордá Он создает дополнительные возмущения при входе жидкости по сравнению с внешним цилиндрическим насадком, рис. 33. Поэтому с гидравлической точки зрения этот насадок имеет худшие коэффициенты: μ = φ = 0,71; ε = 1,0; ζ = 1,0.

Рис. 33
Конические сходящийся и расходящийся насадки В конически сходящемся насадке сжатие струи при входе меньше, чем в цилиндрическом. Однако у этих насадок наблюдается также сжатие струи и при выходе из насадка. Величина этого сжатия, а также коэффициентов, характеризующих этот насадок, зависит от угла конусности Такие насадки дают струю с большими скоростями, поэтому их применяют в качестве сопел турбин, фонтанов, брандспойтов и т.д.
Рис. 34. Конические сходящийся и расходящийся насадки
Конически расходящийся насадок дает малую выходную скорость и вызывает большие потери напора. В случае расходящегося насадка вакуум в сечении оказывается бóльшим, чем в случае сходящегося насадка, поэтому, чтобы получить возможно бóльший расход, следует применять именно его. При угле конусности Казалось бы, насадок плохой, но его очень широко используют в практике при устройстве дорожных труб, водовыпусков оросительных систем, отсасывающих труб турбин ГЭС. Коноидальный насадок. Форма внутренней поверхности этого насадка близка к форме струи, вытекающей из отверстия. Сжатие струи при выходе из насадка отсутствует. Благодаря тому, что стенки насадка имеют плавные очертания, потери в нем весьма малы. Для этого насадка μ=φ =0,97÷0,99; ε= 1,0; ζ= 0,07÷0,03. Его используют наравне с конически сходящимся, но он тяжелее в изготовлении. Кроме указанных насадков, в технике используются и комбинации из них. Расчет насадков. Насадки рассчитываются как отверстия по формулам (43), (47):
Разница в том, что каждый насадок имеет свои коэффициенты Если нужно убавить время опорожнения из резервуара, приставьте насадок к отверстию – и время уменьшится приблизительно на одну треть. Пример: На рис. 35 представлена бетонная плотина, в теле которой имеется круглая водоспускная труба, истечение из этой трубы происходит в атмосферу. Напор равен Н =9,0 м; диаметр трубы d =2,0 м; длина трубы l =10,0 м. Требуется найти расход Q.
Рис. 35 Решение. Необходимо выяснить, будет ли рассматриваемая труба работать, как насадок Вентури. Для этого требуется выполнение двух условий – (63) и (65): - длина насадка должна находиться в пределах: l= (3÷5) d =3·2,0÷5·2,0=(6,0÷10,0) м. Условие выполняется; - максимальный вакуум при истечении через насадок Вентури в атмосферу должен удовлетворять условию (h вак)макс ≤ (h вак)доп . Считают, что для воды (h вак)доп ≈8 м вод. ст. [6]. (h вак)макс=(0,75÷0,8) Н=0,75·9,0÷0,8·9,0=(6,75÷7,2) м. Условие также выполняется. Выполнение обоих условий дает право рассчитать заданную трубу по формуле, относящейся к насадку Вентури:
μн =0,82,
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1826; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.011 с.) |



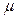 , поскольку на истечение начинают оказывать влияние потери напора по длине. А это значит, что из такой трубы будет меньше вытекать жидкости.
, поскольку на истечение начинают оказывать влияние потери напора по длине. А это значит, что из такой трубы будет меньше вытекать жидкости.

 1).
1). . (66)
. (66) . (67)
. (67) , (68)
, (68)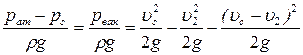 . (69)
. (69) . (70)
. (70)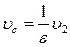 . (71)
. (71)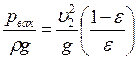 . (72)
. (72)
 . (73)
. (73) . (74)
. (74) =13,34 м.
=13,34 м.
 . Как показывают опыты, наибольший коэффициент расхода μ= 0,946, коэффициент скорости φ =0,963, коэффициент местного сопротивления ζ= 0,08 получается при угле
. Как показывают опыты, наибольший коэффициент расхода μ= 0,946, коэффициент скорости φ =0,963, коэффициент местного сопротивления ζ= 0,08 получается при угле  13°24'.
13°24'.
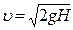 ,
, 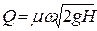 .
. и
и  .
.
 ,
,



