
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения коэффициентов местных сопротивлений в квадратичной области сопротивленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример. Из открытого бака при постоянном напоре H =7м по прямому горизонтальному трубопроводу длиной l =120 м и диаметром d =50 мм вытекает вода в атмосферу, а на расстоянии l1 =110 м установлен вентиль. Определить расход Q при полном открытии вентиля, если коэффициент Кориолиса α =1,1. Построить диаграмму Бернулли (линии Р-Р и E-E). Коэффициент гидравлического трения λ определить по формуле Шифринсона для области квадратичных сопротивлений [2].
Рис. 19
Решение. 1. Если требуется определить υ и
2. Назначаем два сечения: 1-1 в начале заданной системы (уровень воды в баке) и 2-2 в конце трубопровода (выход воды в атмосферу). Плоскость сравнения 0-0 выбираем по оси горизонтальной трубы. Для них: Для этих сечений уравнение Бернулли запишется:
где потери по длине определятся по (21) 3. Из гидравлического справочника [6] выпишем: 4. Подставляя формулы для потерь и коэффициента Дарси, а также справочные значения в (*), получим:
5.Для построения линий Р-Р и Е-Е намечаем дополнительные сечения, проходящие через местные сопротивления: 3-3 – по входу воды в трубу и 4-4 – по вентилю:
а) проводим линию начального напора (или линию полной энергии) от которой откладываются все потери вниз; б) при входе воды в трубу теряется часть энергии на преодоление этого местного сопротивления. Эти потери определяются формулой (30), определим предварительно скорость воды в трубе в) затем вода движется по трубе длиной
откладываем эту потерю в сечении 4-4 от предыдущих потерь и соединяем прямой линией, так как уравнение (21) является уравнением прямой; г) в этом же сечении 4-4 подсчитываем местную потерю напора в вентиле
откладываем вниз от предыдущих потерь; д) на участке от сечения 4-4 до сечения 2-2 поток теряет напор по длине l2 = l-l1 = 120 – 110 = 10 м, потеря на этом участке будет равна Полная потеря напора в рассматриваемой системе определяется
Эту величину откладываем в сечении 2-2 от линии начального напора. В результате такого построения получилась напорная линия E-E; е) для построения пьезометрической линии Р-Р вычислим скоростной напор:
Так как трубопровод постоянного сечения, то линия Р-Р будет параллельна линии E-E и располагаться ниже на величину
что удовлетворяет условию задачи.
ИСТЕЧЕНИЕ ИЗ ОТВЕРСТИЙ, ЧЕРЕЗ НАСАДКИ И ВОДОСЛИВЫ Основное уравнение гидравлики – уравнение Бернулли – было получено в результате решения задачи по истечению жидкости из отверстия. Эта задача сводится к определению скорости истекания и расхода вытекающей жидкости.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.114 (0.011 с.) |




 , следует использовать уравнение Бернулли (17):
, следует использовать уравнение Бернулли (17): .
. – расстояние от сечения 1-1 до плоскости сравнения 0-0;
– расстояние от сечения 1-1 до плоскости сравнения 0-0;  , так как избыточного давления на поверхности воды в баке нет; υ1= 0, так как скорость υ1 в баке несоизмеримо мала по сравнению со скоростью в трубе υ2. Геодезический напор
, так как избыточного давления на поверхности воды в баке нет; υ1= 0, так как скорость υ1 в баке несоизмеримо мала по сравнению со скоростью в трубе υ2. Геодезический напор 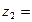 0, так как сечение 2-2 и плоскость сравнения 0-0 совпадают;
0, так как сечение 2-2 и плоскость сравнения 0-0 совпадают;  (вода вытекает в атмосферу); υ2≠ 0 = υ – скорость воды на выходе равна скорости воды в трубе;
(вода вытекает в атмосферу); υ2≠ 0 = υ – скорость воды на выходе равна скорости воды в трубе;  – полные потери напора равны сумме линейных и местных потерь;
– полные потери напора равны сумме линейных и местных потерь;  .
. (*),
(*),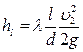 , потери в местных сопротивлениях по (30)
, потери в местных сопротивлениях по (30)  .
. = 0,5;
= 0,5;  = 3 – коэффициенты местных сопротивлений; КЭ= 0,5 мм – эквивалентная шероховатость; формула Шифринсона
= 3 – коэффициенты местных сопротивлений; КЭ= 0,5 мм – эквивалентная шероховатость; формула Шифринсона  .
. ,
, ,
, ,
,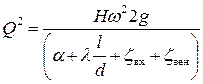 ,
, ,
, .
. 0,00245 м3/с=2,45 л/с.
0,00245 м3/с=2,45 л/с. 1,25 м/с. Тогда
1,25 м/с. Тогда  0,04 м – откладываем эту потерю от линии начального напора в сечении 3-3;
0,04 м – откладываем эту потерю от линии начального напора в сечении 3-3; 110 м до следующего местного сопротивления (сечение 4-4). Определим потери на этом участке по формуле (21):
110 м до следующего местного сопротивления (сечение 4-4). Определим потери на этом участке по формуле (21): 6,08 м,
6,08 м, 0,24 м
0,24 м = 0,55 м, откладываем.
= 0,55 м, откладываем. 0,04 + 6,08 + 0,24 + 0,55 = 6,91 м.
0,04 + 6,08 + 0,24 + 0,55 = 6,91 м. = 0,09 м.
= 0,09 м. . Последняя линия будет показывать изменение давления по длине трубопровода. Поскольку вода вытекает в атмосферу, линия Р-Р заканчивается на оси (т.е. в центре тяжести) потока. Для проверки точности построения E-E определяем напор, которым должна быть обеспечена заданная система
. Последняя линия будет показывать изменение давления по длине трубопровода. Поскольку вода вытекает в атмосферу, линия Р-Р заканчивается на оси (т.е. в центре тяжести) потока. Для проверки точности построения E-E определяем напор, которым должна быть обеспечена заданная система 6,91+0,09=7,0 м,
6,91+0,09=7,0 м,


