
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Местные потери напора в трубопроводахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п. Потери на преодоление местных сопротивлений в наружных сетях водопровода обычно не превышают 10-15%, во внутренних сетях – 30% от потерь напора по длине. Однако местные потери напора в некоторых видах инженерных сетей могут достигать значительной величины: так, например, в системах отопления зданий – до 40%, в воздуховодах вентиляционных систем и пневмотранспорта – до 60-70% от потерь напора по длине. Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления
Общей теории для определения коэффициентов местных сопротивлений, за исключением отдельных случаев, нет. Поэтому коэффициенты местных сопротивлений, как правило, находят опытным путем. Значения их для различных элементов трубопроводов приводятся в технических справочниках. Иногда местные сопротивления выражают через эквивалентную длину прямого участка трубопровода
получаем
или
Рассмотрим внезапное расширение трубы с горизонтальной осью. Потеря напора на внезапное расширение равна
Разность давлений
Это изменение количества движения равно импульсу сил давления. Эти силы следующие: в сечении 1-1, где давление
В соответствии с теоремой о количестве движения приравниваем выражения (а) и (б)
Отсюда после деления на
так как Подставляя правую часть равенства (б) в выражение (а), имеем
или окончательно
т. е. потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Уравнение (106) называется формулой Борда. Для выявления значения коэффициента местного сопротивления из уравнения вынесем за скобки
или
Заменяя скорости через площади живых сечений из уравнения неразрывности
Полученные уравнения (107) и (108) для значения Уравнение (108) представлено в виде графика на рис.
Таким образом, потери напора в диффузоре
Потеря напора на расширение может быть найдена по формуле с введением поправочного коэффициента Ксм, называемого коэффициентом смягчения, который зависит от угла конусности
Коэффициент местного сопротивления в этом случае определится по формуле
Ксм при
Потери напора на трение по длине определяют по формуле
Таким образом, суммарный коэффициент местного сопротивления для диффузора равен
Постепенное сужение трубопровода. Постепенно сужающиеся участки трубопроводов (конфузоры) также нашли широкое применение в практике. При постепенном сужении сечения скорость вдоль трубопровода возрастает, а давление падает. Отрыв потока от стенок в этом случае возможен только на выходе из конфузора в цилиндрическую часть трубопровода. Поэтому при одинаковых гидравлических характеристиках и размерах местные сопротивления в конфузоре меньше, чем в диффузоре. Потери в конфузоре также равны сумме потерь на постепенное сужение и на трение по длине
Потери напора по длине
Потери напора на сужение существенными будут при 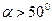 , и их можно определить по формуле , и их можно определить по формуле
где
Здесь График распределения скоростей при структурном режиме изображен на рис. 37. Для определения скоростей по сечению потока теоретическим путем получена следующая формула
где
Для определения скорости в ядре сечения необходимо принять  , тогда , тогда
Расход жидкости определяется по формуле Букингама, полученной теоретически
где Потери напора при движении аномальных (неньютоновских) жидкостей можно определять по уравнению Дарси-Вейсбаха (84), что подтверждено исследованиями Б. С. Филатова. Обычно режим движения турбулентный, и значение При производстве земляных работ получил широкое применение метод гидромеханизации. Грунт размывается струей воды, засасывается землесосом и транспортируется по трубам в отвал или к месту намыва грунта. Смесь воды с размельченным грунтом называется пульпой, или гидросмесью, а трубы по которым перекачивается пульпа, - пульповодами. При некоторой достаточно малой скорости частицы грунта начинают осаждаться и заилять трубопровод. Эта скорость называется критической. Обычные формулы гидравлики, приведенные выше для трубопроводов с водой к пульпопроводам не применимы. Гидравлический расчет пульповодов заключается в определении критических скоростей и потерь напора. Проф. А. П. Юфин предложил следующие эмпирические формулы. Для критической скорости: а) в трубопроводах диаметром до 200 мм
б) в трубопроводах диаметром больше 200 мм
где d – диаметр трубопровода, м; Для потерь напора: а) при критической скорости
б) при скорости выше критической
где Остальные обозначения те же. Контрольные вопросы для СРС: 1. Местные потери напора 2. Внезапное расширение потока 3. Постепенное сужение трубопровода 4. Как определяется потери напора при движении аномальных (неньютоновских) жидкостей?
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.228.55 (0.007 с.) |

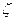 , по формуле
, по формуле .
. . Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям. Приравнивая формулы Дарси-Вейсбаха, имеем
. Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям. Приравнивая формулы Дарси-Вейсбаха, имеем ,
, ,
,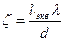 .
. Внезапное расширение потока. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора.
Внезапное расширение потока. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора. .
. найдем, применив уравнение количества движения к отсеку жидкости между сечениями 1-1 и 2-2. За время t через сечения 1-1 и 2-2 протечет масса жидкости
найдем, применив уравнение количества движения к отсеку жидкости между сечениями 1-1 и 2-2. За время t через сечения 1-1 и 2-2 протечет масса жидкости  , количество движения которой в сечении 1-1, где скорость
, количество движения которой в сечении 1-1, где скорость  равно
равно  , а в сечении 2-2 –
, а в сечении 2-2 –  , т. к.
, т. к.  , то изменение количества движения протекшей массы составит
, то изменение количества движения протекшей массы составит . (а)
. (а) , сила давления направлена в сторону течения и равна
, сила давления направлена в сторону течения и равна 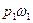 (считается, что давление
(считается, что давление  . Суммарный импульс этих сил за время t составляет
. Суммарный импульс этих сил за время t составляет . (б)
. (б)
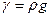 и на
и на  и перемены знаков получаем
и перемены знаков получаем ,
, .
. ,
, ,
,
 ,
, .
. , получим
, получим .
.
 Постепенное расширение трубопровода. Плавно расширяющийся трубопровод – диффузор (рис.) широко применяется в технике. При течении жидкости по диффузору значительно меньше, чем при внезапном расширении. У стенок диффузора также образуются завихрения. Чем больше угол конусности трубопровода, тем больше вихреобразование и соответственно больше потери напора. Потерями по длине в данном случае пренебрегать нельзя.
Постепенное расширение трубопровода. Плавно расширяющийся трубопровод – диффузор (рис.) широко применяется в технике. При течении жидкости по диффузору значительно меньше, чем при внезапном расширении. У стенок диффузора также образуются завихрения. Чем больше угол конусности трубопровода, тем больше вихреобразование и соответственно больше потери напора. Потерями по длине в данном случае пренебрегать нельзя. .
.
 .
. ;
; , a при
, a при  значение коэффициента Ксм следующие:
значение коэффициента Ксм следующие: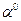
 ……..
……..
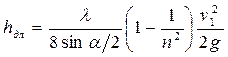 ,
, .
. Наименьшие потери напора в диффузоре получаются при угле расширения его в пределах от 5 до 10°.
Наименьшие потери напора в диффузоре получаются при угле расширения его в пределах от 5 до 10°. .
. можно определять по формуле.
можно определять по формуле.
 ,
, .
. – коэффициент местного сопротивления при внезапном сужении; Ксуж – коэффициент смягчения, учитывающий плавное сужение, который зависит от угла конусности
– коэффициент местного сопротивления при внезапном сужении; Ксуж – коэффициент смягчения, учитывающий плавное сужение, который зависит от угла конусности  ,
, – разность давлений в начале и конце трубопровода;
– разность давлений в начале и конце трубопровода;  – абсолютная вязкость жидкости;
– абсолютная вязкость жидкости;  – длина трубопровода;
– длина трубопровода; 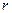 – радиус трубопровода;
– радиус трубопровода;  – расстояние от оси трубопровода до слоя жидкости, у которого определяется скорость;
– расстояние от оси трубопровода до слоя жидкости, у которого определяется скорость; 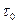 – первоначальное напряжение сдвига.
– первоначальное напряжение сдвига.
 .
. .
. – разность давлении, соответствующая началу движения, определяемая по уравнению
– разность давлении, соответствующая началу движения, определяемая по уравнению  .
. принимают в пределах от 0,017 до 0,025, при этом
принимают в пределах от 0,017 до 0,025, при этом  ;
; ,
,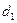 – средний диаметр твердых частиц, мм;
– средний диаметр твердых частиц, мм;  – основание натуральных логарифмов;
– основание натуральных логарифмов;  – удельный вес пульпы;
– удельный вес пульпы; 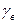 – удельный вес воды;
– удельный вес воды;  ;
;  – так называемая «гидравлическая крупность», т. е. скорость падения частиц в спокойной воде.
– так называемая «гидравлическая крупность», т. е. скорость падения частиц в спокойной воде. ;
; ,
,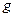 – ускорение свободного падения;
– ускорение свободного падения;  – потери напора в трубопроводе при движении чистой воды при том же расходе;
– потери напора в трубопроводе при движении чистой воды при том же расходе;  – потери напора при движении пульпы с критической скоростью;
– потери напора при движении пульпы с критической скоростью;  .
.


