
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная формула гидростатики.Закон Паскаля. Понятие о напоре.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим абсолютный покой несжимаемой жидкости в поле силы тяжести. Уравнение Эйлера принимает вид
Уравнение непосредственно интегрируется, если плотность жидкости можно считать постоянной вдоль всего объекта, т.е. если не происходит заметного сжатия жидкости под действием внешнего поля. Выберем оси координат, как показано на рис. 2. Поскольку из массовых сил действует только сила тяжести, то
Таким образом, искомая функция р зависит только от одной переменной z; интегрирование последнего равенства дает
где С – произвольная постоянная. Эта формула выражает гидростатический закон распределения давления, состоящий в том, что в тяжелой (подверженной действию силы тяжести) несжимаемой жидкости давление линейно зависит от вертикальной координаты. Чтобы найти постоянную в уравнении, надо использовать какое-нибудь граничное условие. Пусть, например, жидкость покоится в резервуаре (см. рис.2) причем на ее свободной поверхности давление равно р0. Будем это давление называть внешним. Для точек свободной поверхности можем записать
Вычитая это отношение из уравнения, находим
или, обозначив через
где величина Из этой формулы ясно, что всякое изменение внешнего давления Закон Архимеда и его приложение Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела. Pвыт = ρжgVпогр Для однородного тела плавающего на поверхности справедливо соотношение
где: V - объем плавающего тела; Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории. Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называютводоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.5). Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называетсяметацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
Поперечный профиль судна Теперь рассмотрим условия равновесия судна: 1) если h > 0, то судно возвращается в первоначальное положение; Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Контрольные вопросы для СРС: 1. Дайте определение закону Паскаля 2. Напишите основной закон гидростатики 3. Объясните условия равновесия судна 4. Для чего предназначена уравнение Эйлера?
Тема 4. Основные законы движения жидкостей в трубопроводах. Виды движения жидкости Уравнение Д. Бернулли Уравнение Даниила Бернулли является основным уравнением гидродинамики. Ниже разбирается это уравнение для установившегося плавно изменяющегося движения жидкости, с помощью которого решаются основные задачи гидродинамики. Введем понятия удельной энергии элементарной струйки и потока жидкости.
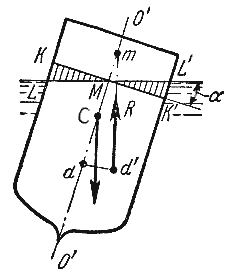
Масса жидкости занимает некоторый объем V, находящийся под давлением р. Потенциальная энергия давления равна рV. Удельная же потенциальная энергия давления равна потенциальной энергии pV, деленной на силу тяжести данного объема gV, т.е.
Полный запас удельной потенциальной энергии массы жидкости равен их сумме, т. е.
Кроме того, масса жидкости т движется со скоростью и и обладает кинетической энергией
Складывая выражения (в) и (г), получим выражение полной удельной энергии элементарной струйки
Здесь
Полная удельная энергия потока Е складывается из удельной потенциальной энергии Для случая установившегося плавно изменяющегося движения жидкости удельная потенциальная энергия во всех точках живого сечения одинакова и равна
Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией Определим среднее значение этой величины в сечении потока. Для этого действительные скорости элементарных струек u1, u2,..., ип заменим средней скоростью потока v; тогда среднее значение удельной кинетической энергии потока в данном сечении равно
Здесь a – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии). Безразмерный коэффициент a представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Если эпюра скоростей в сечении потока близка к прямоугольной, т.е. скорости в разных точках близки к средней, то коэффициент Кориолиса a близок к единице. Если же скорости в сечении значительно различаются между собой, то и коэффициент a оказывается значительно больше единицы.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.009 с.) |

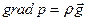 .
. Это уравнение описывает механическое равновесие жидкости. Если внешние силы вообще отсутствуют, то уравнение равновесия гласит просто
Это уравнение описывает механическое равновесие жидкости. Если внешние силы вообще отсутствуют, то уравнение равновесия гласит просто 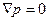 , т.е. р = const – давление одинаково во всех точках жидкости.
, т.е. р = const – давление одинаково во всех точках жидкости.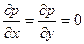 ;
; 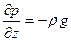 .
.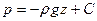 ,
, .
.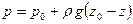
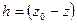 заглубление точки М под свободную поверхность, получим основную формулу гидростатики
заглубление точки М под свободную поверхность, получим основную формулу гидростатики ,
, называется весовым давлением.
называется весовым давлением.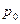 вызывает изменение давления во всех точках покоящейся жидкости на ту же величину. Этот результат известен как закон Паскаля.
вызывает изменение давления во всех точках покоящейся жидкости на ту же величину. Этот результат известен как закон Паскаля.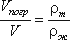
 Удельная энергия элементарной струйки. Напомним, что удельная энергия есть энергия, отнесенная к единице силы тяжести жидкости. Пусть имеем в элементарной струйке частицу массой m, которая обладает некоторой скоростью и, находится под гидродинамическим давлением р, занимает некоторый объем V и находится от произвольной плоскости сравнения о-о на некоторой высоте z (рис.). Масса частицы обладает запасом удельной потенциальной энергии еп, которая складывается из удельных потенциальных энергий положения епол, и давления едав. В самом деле, масса жидкости, поднятая на высоту z, имеет запас потенциальной энергии, равный mgz, где g – ускорение свободного падения. Удельная потенциальная энергия положения равна потенциальной энергии, деленной на силу тяжести жидкости (
Удельная энергия элементарной струйки. Напомним, что удельная энергия есть энергия, отнесенная к единице силы тяжести жидкости. Пусть имеем в элементарной струйке частицу массой m, которая обладает некоторой скоростью и, находится под гидродинамическим давлением р, занимает некоторый объем V и находится от произвольной плоскости сравнения о-о на некоторой высоте z (рис.). Масса частицы обладает запасом удельной потенциальной энергии еп, которая складывается из удельных потенциальных энергий положения епол, и давления едав. В самом деле, масса жидкости, поднятая на высоту z, имеет запас потенциальной энергии, равный mgz, где g – ускорение свободного падения. Удельная потенциальная энергия положения равна потенциальной энергии, деленной на силу тяжести жидкости (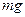 )
)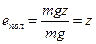 . (а)
. (а)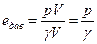 . (б)
. (б) и, учитывая выражения (а) и (б), напишем
и, учитывая выражения (а) и (б), напишем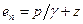 . (в)
. (в)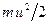 ; но сила тяжести этой массы равна mg, и удельная кинетическая энергия струйки равна
; но сила тяжести этой массы равна mg, и удельная кинетическая энергия струйки равна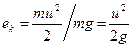 . (г)
. (г) .
.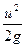 – удельная кинетическая энергия;
– удельная кинетическая энергия;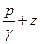 – удельная потенциальная энергия давления и положения.
– удельная потенциальная энергия давления и положения.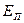 и удельной кинетической энергии Ек потока.
и удельной кинетической энергии Ек потока. . (д)
. (д)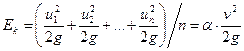 . (е)
. (е)


