
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы сжатия струи. Инверсия струиСодержание книги
Поиск на нашем сайте
На степень сжатия струи могут влиять боковые стенки, а также дно сосуда. В зависимости от удаления отверстия от боковых стенок и дна сосуда различают следующие типы сжатия струи. По характеру сжатие бывает полным, если струя получает сжатие по всему периметру отверстия, и неполным, если струя не имеет бокового сжатия с одной или нескольких сторон, например, когда отверстие примыкает к стенке или ко дну сосуда, которые при этом являются как бы направляющими для вытекания струи (рис. 21, отверстие 3). Полное сжатие может быть совершенным или несовершенным. Совершенным сжатием называют сжатие, возникающее, когда боковые стенки и дно сосуда практически не оказывают влияние на степень сжатия струи (не влияют на истечение). Такое сжатие получается, когда отверстие расположено достаточно далеко от боковых стенок и дна сосуда при условии (рис. 21, отверстие 1): m>3a; n>3a, (48) где m – расстояние от отверстия до боковой стенки; a – длина одной стороны квадратного отверстия; n – расстояние от отверстия до дна сосуда. Как показывают опыты, в этом случае величина ε практически не зависит от размеров m и n. Приводимые в справочниках и учебниках значения коэффициентов расхода относятся к случаям совершенного сжатия.
Рис. 21. К вопросу о сжатии струи Несовершенное сжатие получается при несоблюдении условий (48), т.е. когда отверстие расположено сравнительно близко к боковой стенке или дну сосуда. В этом случае чем меньше размеры m и n, тем меньше сжатие струи и, следовательно, тем больше величина ε (рис. 21, отверстие 2). В случае отверстий одинаковой формы и размеров площадь сжатого сечения при несовершенном сжатии всегда больше площади сжатого сечения при совершенном сжатии. При несовершенном сжатии коэффициент сжатия определяется по формуле:
где п – отношение площади отверстия к площади поперечного сечения потока перед отверстием.
Рис. 22. Инверсия струи
Это происходит благодаря тому, что скорости подхода к отверстию оказываются не одинаковыми для различных участков периметра отверстия. Инверсия вызывается, в основном, действием сил поверхностного натяжения и сил инерции.
Пример изменения формы поперечного сечения струи вдоль течения представлен на рис. 22 (штриховкой показаны сечения струи, намеченные на разных расстояниях от плоскости отверстия).
Истечение через затопленное отверстие при постоянном напоре (под уровень) Так называемое затопленное отверстие представлено на рис. 23.
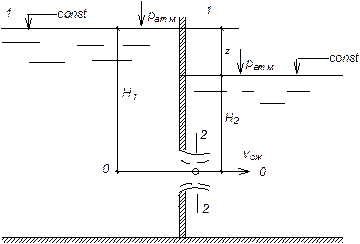
Рис. 23. Истечение из отверстия под уровень
Расход
Значения коэффициентов φ и μ обычно при расчетах принимают такими же, как и при истечении через незатопленное отверстие. Полученные уравнения показывают, что скорость истечения и расход при затопленном отверстии не зависят от глубины погружения отверстия под уровень, а лишь от разности уровней. Пример. В перегородке, разделяющей сосуд на две части, расположено круглое отверстие d1= 5 см. Глубина воды в левой части сосуда h1 =2,5 м. Расход через отверстие Q =3,1 л/с. Определить глубину h2 в правой части сосуда, диаметр d2 отверстия в наружной стенке и скорость υсж в сжатом сечении струи, вытекающей из резервуара. Центры обоих отверстий расположены на высоте а =1 м. Принять коэффициент скорости
Рис. 24 Решение. Согласно (51) расход через первое затопленное отверстие определится:
Согласно (46) расход через второе незатопленное отверстие определится:
Сколько воды перетекает из 1-го отверстия во 2-е, столько же воды вытекает из второго
Можно определить перепад уровней:
Глубина в правой части сосуда Диаметр отверстия в наружной стенке определится из
Согласно (43) скорость в сжатом сечении струи
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 4719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.89 (0.009 с.) |

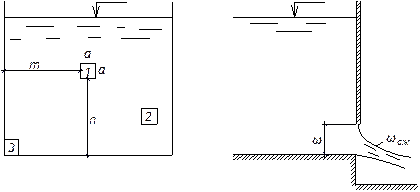
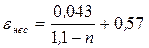 , (49)
, (49)
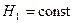 ,
, 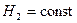 ), получим следующее
), получим следующее
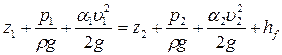 .
.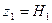 ;
;  ;
; 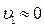 ; α1=α2= 1.
; α1=α2= 1.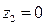 ;
; 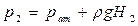 ;
; 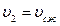 ;
; 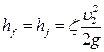 .
.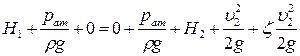 ,
,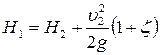 ,
,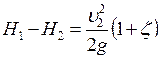 ,
,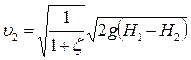 ,
,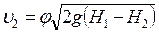 или
или 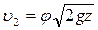 . (50)
. (50)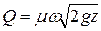 . (51)
. (51)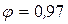 .
.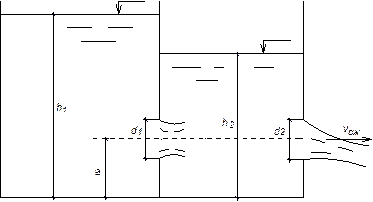
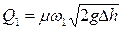 .
.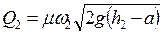 .
.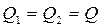 .
.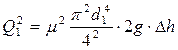 ,
,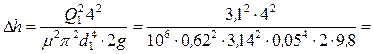 0,33 м.
0,33 м.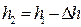 =2,5 – 0,33 = 2,17 м.
=2,5 – 0,33 = 2,17 м.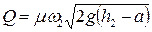 ,
,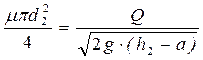 ,
,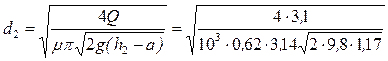 =3,6 см.
=3,6 см.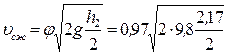 =4,65 м/с.
=4,65 м/с.


