
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод эквивалентных фильтрационных сопротивленийСодержание книги
Поиск на нашем сайте
Данный метод называется методом Борисова и позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки - к одиночно работающей скважине и к одиночно работающей батареи. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простейший физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (4.35) или (4.36) с законом Ома I=U / R, где I - ток, U - разность потенциалов и R - сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (4.35), который состоит из двух слагаемых. Если в (4.35) оставить только первое слагаемое, то оно будет выражать дебит в прямолинейно-параллельном потоке через площадь величиной nhs на длине L. Т.о. первое слагаемое выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Борисов назвал эту часть фильтрационного сопротивления - внешним фильтрационным сопротивлением
Оставим теперь в (4.35) только второе слагаемое. В этом случае получим аналог формулы Дюпюи для суммарного дебита n скважин при плоскорадиальном течении и в предположении, что каждая скважина окружена контуром питания длиной s. Т.о. второе слагаемое выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин, и по Борисову оно получило название внутреннего
На внешнее и внутреннее фильтрационные сопротивления разделяется также полное фильтрационное сопротивление кольцевой батареи
Здесь r выражает фильтрационное сопротивление потоку от контура питания к кольцевой батареи радиуса а в предположении, что поток плоскорадиален и батарея заменена галереей. Внутреннее сопротивление r / - это сопротивление плоскорадиального потока от воображаемого контура окружности длиной 2pа/n к скважине. Величина 2pа/n - длина дуги сектора радиуса а, который содержит одну из скважин батареи. Электрическая схема в случае одной батареи (рис.4.12) имеет вид (рис.4.13). На рис.4.12 затемнены области внутреннего сопротивления.
Рассмотрим случай притока к n эксплуатационным и нагнетательным батареям скважин и составим схему сопротивлений. Предположим, что скважины i-ой батареи имеют забойные потенциалы jсi (i=1,...,n), пласт имеет контурные потенциалы jк1 и jк2 (рис. 4.14). Пусть jк1 > jк2. Очевидно, поток от контура питания к первому ряду скважин будет частично перехватываться первой батареей и частично двигаться ко второй. Поток ко второй батарее будет частично перехватываться второй батареей, частично двигаться к третьей и т.д. Этому движению отвечает разветвленная схема фильтрационных сопротивлений (рис. 4.15). Расчет ведется от контура с большим потенциалом к контуру с меньшим потенциалом, а сопротивления рассчитываются по зависимостям: * прямолинейная батарея * круговая батарея
где Li - расстояние между батареями (для i=1 - L1=Lк1); ri - радиусы батарей (для i=1 - r0=rк); ki - число скважин в батареи. Дальнейший расчет ведется, как для электрических разветвленных цепей, согласно законам Ома и Кирхгоффа:
Следует помнить, что для последовательных сопротивлений r=Sri, а для параллельных -
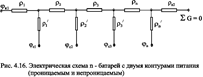
Если одна из границ непроницаема, то расход через неё равен нулю. В этом случае в соответствующем узле схемы фильтрационных сопротивлений задаётся не потенциал, а расход. На рис. 4.16 показана схема в случае непроницаемости второго контура. Вместо потенциала jк2, показанного на рис.4.15, здесь в узле задано условие SGi =0. Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами. Если расстояние между скважинами много больше расстояния между батареями, то расчет надо вести по общим формулам интерференции скважин или использовать другие виды схематизации течения, например, заменить две близко расположенные соседние батареи скважин с редкими расстояниями между скважинами (рис. 4.17а) эквивалентной одной батареей - с суммарным числом скважин и проведенной посредине (рис.4.17b).
Интерференция скважин. Разработка нефтяных и газовых месторождений осуществляется множеством скважин, каждая из которых имеет потенциал на стенке скважины и на контуре питания. Суммарный дебит скважин должен обеспечить заданный темп и объем отбора нефти или газа из месторождения. При этом возникают гидродинамические задачи: - определить давление на забое скважины при заданных дебитах; - определить дебиты при заданных забойных давленях.
При решении гидродинамических задач необходимо учитывать, что при работе скважин наблюдается их взаимное влияние друг на друга (т. е. интерференция скважины), в результате которой средний дебит скважин при увеличении их числа падает, поэтому при вводе в эксплуатацию новых скважин суммарная добыча нефти на месторождении растет не прямо пропорционально числу скважин, а значительно медленнее как показано на графике (рис 1.) Рассмотрим некоторую точку и расположим вокруг нее пять стоков. Задача состоит в том, чтобы вычислить распределение потенциала и направление скорости фильтрации в пласте от каждого стока при условии, что ввод стоков осуществляется от первого до пятого (т. е. по порядку). Первый сток работает с интенсивностью q1. Тогда значение потенциала Ф для первого стока определится следующим образом: Ф01(r01) = (q1/2π)·lnr01 + C1 Для второго стока: Ф02(r02) = (q2/2π)·lnr02 + C2 и т.д. для др. стоков. Суммарный потенциал в нулевой (рассматриваемой) центральной точке определится след. образом: Ф(О) = (q1/2π)·lnr01 + C1 Выводы: - в результате интерференции скважин работающих в одинаковых условиях прирост суммарного дебита уменьшается; - чем ближе скважины друг к другу в цепочке, тем сильнее сказывается эффект интерференции, сл-но суммарный дебит меньше; - на суммарную добычу большое влияние оказывает расстояние до контура питания или цепочки нагнетательных скважин; - при приближении нагнетательных скважин к добывающим эффект интерференции уменьшается, сл-но суммарный дебит увеличивается. 13. Основные технологические ограничения в разработке нефтяных месторождений прежде всего распространяются на давления и дебиты (приемистость) добывающих (нагнетательных) скважин, и соответственно они касаются технических характеристик применяемого на промысле оборудования. Для того чтобы оборудование функционировало без сбоев и как можно большее время необходимо контролировать постоянно изменяющиеся характеристики залежей углеводородов. Например, при фонтанной эксплуатации скважины возможно накопление газа в затрубном пространстве и как следствие возможен периодический прорыв газа к башмаку фонтанных труб, соответственно работа скважины нарушается. Такое явление называют пульсацией. А если в добываемой продукции содержится песок, то изменение забойного давления способствует пробкообразованию. Для обеспечения нормальной работы такой скважины необходимо контролировать рост давления в межтрубном пространстве. Также при любом способе эксплуатации, применяемом на месторождении, необходимо контролировать забойные давления и динамические уровни работы скважины для того, чтобы недопустить выход из строя и обеспечить нормальную работу добывающего оборудования (УШГН, ЭЦН и т.п.). Ограничения норм отбора нефти из скважин: Максимально допустимый отбор который скважина может дать, чаще всего недопустим, так как это влечет за собой нерациональный расход пластовой энергии, неполное извлечение нефти и может вывести скважину из строя вследствие смятия колонны или разрушения пласта. Поэтому для каждой скважины устанавливается своя норма отбора – максимальный дебит, допускаемый условиями рациональной эксплуатации. Для газовых залежей норму отбора устанавливают по началу выноса песка струей газа или устанавливают такой отбор, при котором не подтягивается вода. Для систем ППД вводят ограничения для насосных агрегатов, в зависимости от типа коллекторов. Вводятся также ограничения на физико-химические свойства закачиваемой воды, наличие механических примесей и т.д.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.36 (0.007 с.) |

 . 4.37
. 4.37 . 4.38
. 4.38
 . 4.39
. 4.39
 4.40
4.40 4.41
4.41

 - алгебраическая, сумма сходящихся, в узле дебитов равна нулю, если считать подходящие к узлу дебиты положительными и отходящие - отрицательными.
- алгебраическая, сумма сходящихся, в узле дебитов равна нулю, если считать подходящие к узлу дебиты положительными и отходящие - отрицательными. - алгебраическая сумма произведения дебитов на сопротивления (включая и внутреннее) равна алгебраической сумме потенциалов, действующих в замкнутом контуре. При этом и дебиты и потенциалы, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а направленное навстречу обходу отрицательным.
- алгебраическая сумма произведения дебитов на сопротивления (включая и внутреннее) равна алгебраической сумме потенциалов, действующих в замкнутом контуре. При этом и дебиты и потенциалы, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а направленное навстречу обходу отрицательным.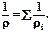


 где Сi – постоянная интегрирования потенциалов
где Сi – постоянная интегрирования потенциалов


