
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики многофазной фильтрацииСодержание книги
Поиск на нашем сайте
Углеводородные системы могут быть гомо- и гетерогенными. В гомогенной системе все её части имеют одинаковые физические и химические свойства. Составляющие гомогенной системы (называемые компонентами) «размазаны» по пространству и взаимодействуют на молекулярном уровне. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза – это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами. Смесь воды, нефти и газа в пласте – типичный пример гетерогенной среды. Главными характеристиками движения многофазной среды являются насыщенность и скорость фильтрации каждой фазы. Насыщенностью si порового пространства i - ой фазой называется доля объема пор DVi, занятая этой фазой в элементарном объеме:
где n – число фаз. Очевидно, что:
Таким образом, в n - фазной системе имеется ( n -1 ) независимая насыщенность. При исследовании фильтрации смеси двух фаз используется лишь одна из насыщенностей, которая обозначается в дальнейшем s (это насыщенность вытесняющей фазы, обычно воды). Движение каждой из фаз характеризуется вектором скорости фильтрации ui данной фазы, который (по аналогии со скоростью фильтрации однородной жидкости) определяется как вектор, проекция которого на некоторое направление L равна отношению объемного расхода Qi данной фазы к площадке Wi, перпендикулярной к указанному направлению:
Площадка Wi пересекает как твердую, так и подвижные фазы. При изучении сложных фильтрационных процессов возникает необходимость в построении моделей многофазных (гетерогенных) систем, в которых каждая фаза, в свою очередь, моделируется многокомпонентной гомогенной смесью. При этом между компонентами возможны химические реакции, переход компонентов из одной фазы в другую, процессы адсорбции, диффузии и др. В дальнейшем для простоты и лучшего понимания физической сути происходящих процессов ограничимся рассмотрением двухфазной фильтрации (например, нефти и воды или воды и газа). При совместном течении двух фаз в пористой среде, по крайней мере, одна из них образует систему, граничащую со скелетом породы и частично с другой жидкостью. Из-за избирательного смачивания твердой породы одной из жидкостей площадь контакта каждой из фаз со скелетом пористой среды значительно превышает площадь контакта фаз между собой. Это позволяет предположить, что каждая фаза движется по занятым ею поровым каналам под действием своего давления независимо от других фаз, т. е. так, как если бы она была ограничена только твердыми стенками. При этом, естественно, сопротивление, испытываемое каждой фазой при совместном течении, отлично от того, которое было бы при фильтрации только одной из них. Опыты показывают, что расход каждой фазы растет с увеличением насыщенности и градиента давления. Закон фильтрации каждой из фаз при учете силы тяжести по аналогии с законом Дарси можно записать в следующем виде:
Здесь k – абсолютная проницаемость пласта, определяемая по данным о фильтрации однородной жидкости; mi – коэффициент динамической вязкости фаз; pi – давление в фазах; ri – плотность фаз; g – вектор ускорения свободного падения; ki(s) – относительные фазовые проницаемости, определяемые экспериментально; si – насыщенность одной из фаз.
Рисунок 15.1 – Зависимость относительных проницаемостей от насыщенности
Будем считать, что s = s1 есть насыщенность вытесняющей (или более смачивающей) фазы. Тогда из (15.2) имеем s 2 = 1- s 1. Понятие относительной фазовой проницаемости ki(s), играет важную роль при изучении совместного течения нескольких жидкостей в пористой среде. Будем исходить из условия, что относительные проницаемости являются однозначными функциями насыщенностей и не зависят от скорости фильтрации и отношения вязкостей движущихся фаз. На рисунке 15.1 приведены типовые кривые относительных фазовых проницаемостей для двухфазной смеси (пунктир на рисунке относится к случаю, когда первая фаза является газом). На этом графике показаны безразмерные относительные фазовые проницаемости k 1 и k 2; sА – связанная компонента первой, более смачивающей фазы (для воды обычно около 20 %). Характерная несимметричная форма кривых относительной проницаемости объясняется тем, что при одной и той же насыщенности более смачивающая фаза занимает преимущественно мелкие поры и относительная проницаемость у неё меньше. При малых насыщенностях часть каждой из фаз находится в несвязном состоянии в виде изолированных мелких капель или целиков и не участвует в движении. Поэтому, начиная с некоторой насыщенности, каждая фаза полностью переходит в несвязное состояние и её относительная проницаемость становится равной нулю, т. е. k 1(s) = 0 при s <sA, k 2(s) = 0 при s > 1- sA. Движение этой фазы может происходить только, если s > sА . Для второй фазы связанная компонента равна 1 - sA. Заметим, что хотя речь идет о совместной фильтрации двух несмешивающихся жидкостей, приходится различать вытесняющую и вытесняемые фазы, т. к. относительные проницаемости различны в зависимости от того, какая из фаз (более или менее смачиваемая) первоначально заполняла пористую среду, т. е. существует гистерезис относительных проницаемостей. Сумма относительных проницаемостей для каждого фиксированного значения s меньше 1:
Причем, присутствие связанной смачивающей фазы мало влияет на течение не смачивающей жидкости, тогда как присутствие остаточной не смачивающей фазы значительно «стесняет» движение смачивающей фазы. Введенные понятия можно обобщить на случай совместного движения трех несмешивающихся флюидов: нефти, газа и воды. Если обозначить эти флюиды индексами «н», «г» и «в», то можно ввести относительные проницаемости, точно так же как это было сделано для двух жидкостей. При этом фазовые проницаемости являются уже функциями двух независимых насыщенностей и определяются из треугольных диаграмм (рисунок 15. 2).На треугольной диаграмме показаны границы преобладания фаз. Из диаграммы видно, что при газонасыщенности более 35 % поток состоит только из газа, более тёмная область показывает на наличие всех фаз. По диаграмме можно определить, какие компоненты движутся в пласте при данном соотношении величин насыщенности пор фазами.
Рисунок 15.2 – Диаграмма для определения границ преобладания потоков различных фаз при трёхфазном движении
На основании экспериментов можно считать, что относительная фазовая проницаемость в многофазном потоке почти не зависит от вязкости жидкости, ее плотности, внутрижидкостного натяжения, градиента давления. Характерные особенности многофазной фильтрации связаны также с влиянием поверхностного натяжения. Давления в фазах р 1 и р 2 вообще говоря, не равны друг другу из - за капиллярных эффектов, приводящих к скачку давления на границе раздела фаз. Так что характер зависимостей определяется различной степенью смачивания твердых зерен породы фазами. Причем оказывается, что относительная проницаемость зависит только от водонасыщенности наиболее смачивающей фазы – воды и почти не зависит от нефте - и газонасыщенности: р 2 - р 1 = рк, (15.5) где рк – капиллярное давление (или капиллярный скачок). Большее давление будет на стороне жидкости, не смачивающей твердые зерна породы. Предполагается, что капиллярное давление при совместном течении жидкостей совпадает с капиллярным давлением в равновесном состоянии для того же значения насыщенности и при одном и том же направлении её изменения (увеличении или уменьшении). Поэтому считают, что при движении капиллярное давление можно представить в виде известной экспериментальной функции насыщенности (рисунок15.3):
где aп – коэффициент межфазного поверхностного натяжения; q – статический краевой угол смачивания между жидкостями и породой; m – пористость; J(s) – безразмерная функция Леверетта.
Рисунок 15.3 – Зависимость функции Леверетта от насыщенности: 1 – кривая вытеснения; 2 – кривая пропитки; А – остаточная насыщенность вытесняемой жидкости
Процессы многофазной фильтрации идут по-разному в зависимости от характерного времени фильтрационного процесса и от размеров области течения. Капиллярные силы создают в пористой среде перепад давления, величина которого ограничена и не зависит от размеров области фильтрации. Вместе с тем перепад внешнего давления, создающего фильтрационный поток между двумя точками, пропорционален скорости фильтрации и расстоянию между этими точками. Если размеры области малы, то при достаточно малых скоростях фильтрации капиллярные силы могут превзойти внешний перепад давления. Напротив, если рассматривается движение в очень большой области (например, в целой нефтяной или газовой залежи), то влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз. Взаимное торможение фаз, благодаря которому относительные фазовые проницаемости не пропорциональны соответствующим насыщенностям, обусловлено, прежде всего капиллярными эффектами. Когда можно пренебречь капиллярным скачком рк (s) капиллярность косвенно учитывается самим видом опытных кривых относительных проницаемостей ki (s). Таким образом, при описании многофазной фильтрации увеличивается число параметров, подлежащих определению. Наряду с неизвестными давлениями pi в фазах и скоростями фильтрации фаз ui появляются новые неизвестные насыщенности si и концентрации отдельных компонентов. Это усложняет теоретическое исследование.
Исходные уравнения многофазной фильтрации Будем для простоты рассматривать совместное изотермическое течение двух фаз (воды и нефти) в однородной пористой среде без фазовых переходов и химических реакций. Система уравнений, описывающая совместную фильтрацию фаз, строится на основе уравнений неразрывности для каждой фазы, уравнений движения (закона фильтрации) и соответствующих замыкающих соотношений. Уравнения неразрывности: первой смачивающей фазы: второй фазы (нефти, газа): Если вытесняемая и вытесняющая фазы – слабосжимаемые упругие жидкости, то влиянием сжимаемости на распределение насыщенности можно пренебречь, так как время перераспределения давления за счет сжимаемости жидкостей, по крайней мере, на два порядка меньше, чем время вытеснения. Отсюда следует, что нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. В некоторых случаях можно считать несжимаемым и газ в пластовых условиях. Если жидкости и пористую среду можно рассматривать как несжимаемые, то вместо уравнений (15.7) и (15.8) имеем:
Уравнения движения для многофазной фильтрации. При записи закона фильтрации предполагают, что в любой точке каждая из фаз находится в термодинамическо равновесном состоянии. Тогда для течения двухфазной смеси можно ввести в рассмотрение относительные проницаемости ki(s) и капиллярное давление рк(s), зависящее только от насыщенности. При рассмотрении однонаправленной фильтрации без учета гистерезисных явлений закон движения (15.4) запишется:
Связь между давлениями в фазах определяется равенствами (15.5) и (15.6):
Для замыкания полученной системы уравнений необходимо задать связи параметров, связывающих свойства фаз и пористой среды, с давлением (уравнения состояния флюидов ). При изотермических условиях фильтрации плотность и вязкость каждой из фаз определяются давлением в данной фазе: ri = ri(pi), mi = mi(pi), (i = 1, 2 ). (15.12) Пласт будем считать недеформируемым. Таким образом, получена замкнутая система уравнений (15.7), (15.8), (15.10), (15.11) и (15.12) для определения всех неизвестных параметров: насыщенности s, давления pi, скорости фильтрации ui,. плотности r i и вязкости m i фаз. Постановка и решение задач на основе полной системы уравнений фильтрации неоднородных жидкостей затруднительны ввиду сложности самих уравнений, а также формулировки краевых условий, в частности разрыва капиллярных сил на границах пористой среды (так называемых концевых эффектов), роль которых недостаточно изучена. Анализ одномерных двухфазных потоков позволяет выявить основные эффекты и характерные особенности совместной фильтрации жидкостей.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.149.144 (0.011 с.) |

 , i = 1, 2,…, n (15.1)
, i = 1, 2,…, n (15.1) . (15.2)
. (15.2) , i = 1, …. n. (15.3)
, i = 1, …. n. (15.3) . (15.4)
. (15.4)
 , 0 < s <1.
, 0 < s <1.
 , (15.6)
, (15.6)
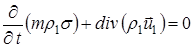 ; (15.7)
; (15.7) . (15.8)
. (15.8) ,
, 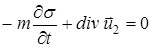 . (15.9)
. (15.9) . (15.10)
. (15.10) . (15.11)
. (15.11)


