Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимости плотности и вязкости флюидов от давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Различают жидкости: а) несжимаемую: r = соnst. (5.7) в) упругую, имеющую место при нестационарных процессах отбора нефти за счёт расширения её объёма при снижении давления:
где bж – коэффициент объёмного расширения жидкости,
Vж – объём жидкости; bж = (7 – 30)10-10 Па-1 – для нефти и (2,7 – 5)10-10Па-1 для пластовой воды;
г) сжимаемую жидкость – газ, имеющую место при разработке газовых и газоконденсатных залежей. До рпл < 9 МПа и D р < 1 МПа можно использовать уравнение состояния совершенного газа: р = r R T, (5.10) где R – газовая постоянная, Т – температура. Совершенный газ – это газ, молекулы которого не имеют объёма и не взаимодействуют между собой. При изотермическом процессе (Т= const) используют соотношение: r = rcт р/ рст. (5.11) Если рпл > 9 МПа, то надо использовать обобщённое уравнение состояния реального газа: Р = zr R T, (5.12) где z – коэффициент сверхсжимаемости, являющийся функцией давления при изотермическом течении
До давления меньшего давления насыщения жидкости газом ее вязкость можно принимать не зависящей от давления, а при больших значениях давления вязкость определяется так:
Зависимость пористости и проницаемости пласта от давления Пористость связана с давлением между частицами пористой среды – эффективным давлением sэф, передающимся через поверхности контакта зёрен породы. Считается, что: sэф+рпл=ргорн=const. (5.15) Здесь рпл – поровое давление; ргорн=rгорн g H – горное давление, возникающее под действием масс горных пород над кровлей пласта средней плотности rгорн; Н – глубина залегания пласта. При разработке рпл падает и, согласно (5,15), растёт sэф. Увеличение sэф приводит к деформации пласта, а именно, переупаковке зёрен в сторону уплотнения и даже их разрушения. Принимается, что:
где bт – коэффициент объёмной упругости породы с пределами изменения (0,3 – 2)10-10Па-1. В связи с уменьшением пористости при увеличении давления, также по аналогичному закону уменьшается проницаемость:
При Dр < 10 МПа показатель в (5.16, 5.17) меньше 1 и, следовательно, данные экспоненциальные зависимости можно разложить в ряд Тейлора. Ограничиваясь первыми двумя членами, получим:
где ψ – общее обозначение вышеприведённых параметров. ЛЕКЦИЯ 6 УСТАНОВИВШАЯСЯ ПОТЕНЦИАЛЬНАЯ ОДНОМЕРНАЯ ФИЛЬТРАЦИЯ Виды одномерных потоков Одномерным называется поток, в котором параметры являются функцией только одной пространственной координаты, направленной по линии тока. К одномерным потокам относятся: 1) прямолинейно-параллельный: 2) плоскорадиальный; 3) радиально-сферический. В прямолинейно-параллельном потокетраектории частиц жидкости – параллельные прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями перпендикулярными траекториям. Законы движения в каждой горизонтальной плоскости такого фильтрационного потока идентичны, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат х.
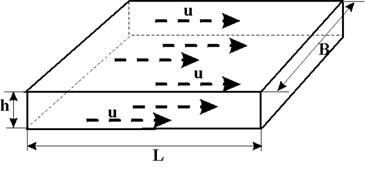
Рисунок 6.1– Схема прямолинейно-параллельного потока в пласте
Примеры такого потока следующие: Пласт (рисунок 6.1) имеет в плане полосообразную форму шириной B и длиной L, толщина пласта h постоянна, граничный контур непроницаем и непроницаемы кровля и подошва пласта. Батарея эксплуатационных скважин расположена параллельно начальному контуру нефтеносности. Приближение к прямолинейно-параллельному потоку тем больше, чем меньше расстояние между скважинами, а если заменить батарею сплошной прямолинейной выработкой – галереей, то движение жидкости к галерее будет строго прямолинейно-параллельным. Прямолинейно-параллельным будет поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (поскольку угол схождения векторов скоростей при этом мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы. В лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой средой, поток также будет прямолинейно-параллельным. В плоскорадиальном потокетраектории частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости. Примеры плоскорадиального потока. Горизонтальный пласт постоянной толщины h и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рисунок 6.2), т. е. вскрыт на всю толщину и забой полностью открыт. Для эксплуатационной скважины поток радиально-сходящийся, а для нагнетательной – радиально-расходящийся. Плоскорадиальным потоком будет занято пространство от стенки скважины до контура питания.
Рисунок 6.2 – Схема плоскорадиального потока в пласте
Вблизи гидродинамически несовершенной скважины линии тока искривляются и поток можно считать плоскорадиальным только при некотором удалении от скважины. Круговая батарея эксплуатационных скважин – поток плоскорадиален на некотором удалении от батареи, жидкость движется как бы к укрупнённой скважине радиуса, равного радиусу окружности батареи. В радиально-сферическом потоке (рисунок 6.3)траектории частиц жидкости – прямолинейные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным. Такой поток может реализовываться, когда скважина только вскрывает плоскую горизонтальную, непроницаемую кровлю пласта. Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта. Последний вид потока встречается редко.
Рисунок 6.3 – Схема радиально-сферического потока в пласте
Одномерные потоки играют большую роль при решении многих задач нефтегазопромысловой практики. Они лежат в основе исследований закономерностей течения жидкости в пласте в зависимости от принятой системы разработки или от конструктивных особенностей скважин. Моделируя одномерные потоки, мы схематизируем реальные пласты и течения жидкости. Такие схемы не только воспроизводят, хотя и приближенно, простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из его простейших видов.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.15 (0.007 с.) |

 (5.8)
(5.8) (5.9)
(5.9) (5.13)
(5.13) (5.14)
(5.14) (5.16)
(5.16) (5.17)
(5.17)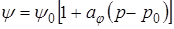 , (5.18)
, (5.18)