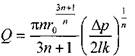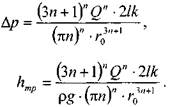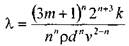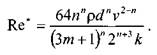Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение вязкопластических жидкостей в трубах.Содержание книги
Поиск на нашем сайте
Для того, чтобы вязкопластичная жидкость начала перемещаться необходимо создать между начальным и конечным сечениями участка трубы длиной / некотурую разность напоров, при которой будет преодолена величина начального статического напряжения сдвига Поскольку в начальный момент времени силы трения будут возникать только у стенок трубы, то уравнения равновесия можно запмсать в следующем виде:
Необходимая разность напоров между началом и концом участка трубы определится следующим образом:
Таким образом, при превышении разности напоров расчётную величину жидкость начнёт двигаться по трубе, причём характер (режим) её движения будет зависеть от величины Условие в структурном режиме, при этом под величиной статического напряжения сдвига следует понимать величину соответствующую длительному покою жидкости, т.е. с учётом проявления тиксотропных свойств жидкости. Структурный режим течения жидкости предполагает наличие вдоль стенок трубы сплошного ламинарного слоя жидкости; в центральной части трубы наблюдается ядро те- чения, где жидкость движется, сохраняя прежнюю свою структуру, т.е. как твёрдое тело. Размеры центрального ядра течения (радиус При увеличении А/г размеры ламинарной зоны будут постепенно увеличиваться за счёт уменьшения размеров ядра течения пока структурный режим не перейдёт в полностью ламинарный режим движения жидкости. В дальнейшем ламинарный режим постепенно сменится турбулентным режимом движения жидкости. Для определения закона распределения скоростей по сечению потока при структурном режиме движения жидкости запишем некоторую функцию для касательных напряжений в соответствии с
Тогда распределение скоростей по сечению трубы можно выразить следующим образом:
где:
И окончательно:
Для определения скорости в ядре течения примем (структурной части потока жидкости). Тогда величина скорости в этом ядре течения (скорости в ядре течения одинаковые равны)
Расход жидкости при структурном движении можно определить, используя известные соотношения дл круглой трубы:
Интегрируя уравнение в пределах от
Последнее уравнение, известное как формула Букингама, можно упростить:
где: тельнве напряжения в ней достигают величины касательного напряжения сдвига. Если пренебречь величиной второго члена ввиду его малости, получим:
Комплексный параметр Таким образом, при расчётах движения вязкопластических жидкостей можно пользоваться уравнениями для ньютоновских жидкостей, заменяя в уравнениях величину числа Рейнольдса Re на обобщённый критерий Рейнольдса Турбулентный режим течения жидкости. Характер течения вязкопластических жидкостей существенно не отличается от турбулентного потока ньютоновских жидкостей. Отличие состоит в количественных соотношениях между величинами коэффициентов трения и числом Рейнольдса. Так коэффициент трения может быть выражен как функция обобщённого числа Рейнольдса (в общем виде) следующим образом:
где: В и п - некоторые параметры, устанавливаемые по данным экспериментов. Так по данным экспериментов Б.С. Филатова величины коэффициентов В и п принимаются следующими: - для неутяжелённого глинистого раствора В = 0,1 и п = 0,15, - для утяжелённого глинистого раствора В = 0,0025 и п = -0,2. Для расчёта трубопроводов при ждижении по ним глинистых и цементных растворов можно пользоваться формулой Б.И. Мительмана:
В практике работы горных предприятий не редки случаи, когда приходится транспортировать неньютоновские жидкости в безнапорных потоках (самотёком), в лотках, по желобным системам. Характер течения вязкопластичных жидкостей в открытых каналах при структурном режиме идентичен аналогичному и напорному потокам такой жидкости в круглых трубах. Т.е. при структурном режиме течения жидкости также выделяется центральное ядро течения, где жидкость движется как твёрдое тело, сохраняя свою первонв-чальную структуру. Ядро течения подстилается непрерывным ламинарным слоем жидкости. Течению таких жидкостей по открытым каналам прямоугольного профиля посвящены работы Р.И. Шищенко. По данным его исследований расход вязкопластичной жидкости при структурном режиме движения может быть определён по приближённой формуле:
где:
/ - уклон дна канала,
Для жидкостей, подчиняющихся степенному реологическому закону, функция напряжения сдвига будет иметь следующий вид:
Тогда распределение скоростей в сечение потока будет соответствовать следующей зависимости:
Интегрируя это уравнение, найдём:
Отсюда можно получить выражение для расхода жидкости:
Отсюда определим величину перепада давления, обеспечивающую движение жидкости и соответствующую величину потерь напора на трение.
Сопоставляя полученное выражение с формулой Дарси-Вейсбаха, найдём величину коэффициента трения и обобщённый критерий Рейнольдса:
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.119 (0.007 с.) |

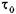 . При этом жидкость отрывается от стенок трубы и первоначально движется на подвижном ламинарном слое, сохраняя свою прежнюю пространственную структуру, т.е. с одинаковыми скоростями по всему отсеку потока. Разрушение этой структуры происходит позже и при некотором превышении напора.
. При этом жидкость отрывается от стенок трубы и первоначально движется на подвижном ламинарном слое, сохраняя свою прежнюю пространственную структуру, т.е. с одинаковыми скоростями по всему отсеку потока. Разрушение этой структуры происходит позже и при некотором превышении напора.
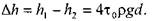
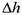 . При движении вязкопластичной жидкости возможны три режима течения её: структурный, ламинарный и тутбулентный.
. При движении вязкопластичной жидкости возможны три режима течения её: структурный, ламинарный и тутбулентный.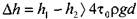 является необходимым для начала движения жидкости
является необходимым для начала движения жидкости ) может быть определён исходя из следующего соотношения:
) может быть определён исходя из следующего соотношения: 
 формулой Бингама:
формулой Бингама: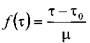
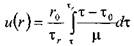 ?
?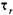 - касательное напряжение на стенке трубы радиуса
- касательное напряжение на стенке трубы радиуса 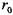 ,
,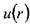 - скорость жидкости на расстоянии
- скорость жидкости на расстоянии  от центра трубы. После интегрирования этого уравнения получим:
от центра трубы. После интегрирования этого уравнения получим: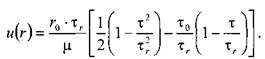
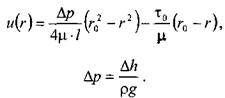
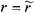 , где
, где 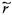 - радиус ядра течения
- радиус ядра течения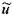 : '
: '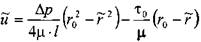
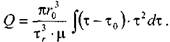
 до
до 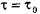 , получим:
, получим: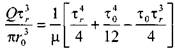 5 f
5 f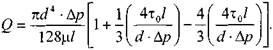
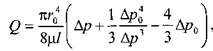
 - разность давлений при начале движения жидкости, когда каса-
- разность давлений при начале движения жидкости, когда каса-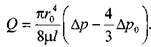
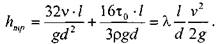
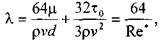 * где:
* где:  - обобщённый критерий Рейнольдса.
- обобщённый критерий Рейнольдса.
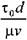 = Sen носит название числа Сен-Венана.
= Sen носит название числа Сен-Венана.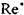
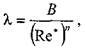
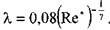 при: Re* =2500-40000. 12.3. Движение вязкопластичных жидкостей в открытых каналах
при: Re* =2500-40000. 12.3. Движение вязкопластичных жидкостей в открытых каналах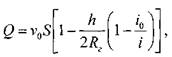
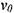 - скорость течения ядра потока
- скорость течения ядра потока 
 - площадь живого сечения канала шириной b и глубиной заполнения h,
- площадь живого сечения канала шириной b и глубиной заполнения h,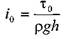 - гидравлический уклон, соответствующий началу течения жидкости,
- гидравлический уклон, соответствующий началу течения жидкости,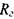 - гидравлический радиус живого сечения потока. 12.4. Движение неньютоновских жидкостей, подчиняющихся степенному реологическому закону, по трубам
- гидравлический радиус живого сечения потока. 12.4. Движение неньютоновских жидкостей, подчиняющихся степенному реологическому закону, по трубам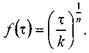
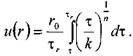
 , или:
, или: