
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение неразрывности для элементарной струйки жидкостиСодержание книги
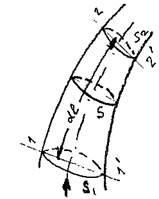
Поиск на нашем сайте Выделим в элементарной струйке жидкости двумя сечениями 1 - Г и 2 - 2' малый отсек жидкости длиной dl. Объём жидкости внутри выделенного отсека
Масса жидкости, вытекшая за это же время через противоположное сечение отсека: 1 В данном разделе для удобства записи вместо принятых ранее обозначений площади сечения элементарной струйки жидкости dS и элементарного расхода жидкости dQ используются обозначения: S и Q.
За тот же интервал времени масса жидкости внутри отсека изменится на величину: ^ * откуда
Окончательно формула может быть представлена в виде
При установившемся движении жидкости (р = const) уравнение неразрывности примет вид:
Элементы кинематики вихревого движения жидкости Поступательному движению жидкости часто сопутствует вихревое движение, вызванное вращением элементарного объёма жидкости вокруг некоторой оси Такое вращение жидкости называется вихрем; угловая скорость этого элементарного объёма является основной характеристикой вихря Касательная в любой точке вектора вихря - вихревая линия Поверхность образованная вихревыми линиями, проведенными через точки замкнутого контура, называется вихревой трубкой Прямолинейную вихревую трубку с бесконечно малой площадью сечения можно рассматривать как вращающийся твердый цилиндр, окружная скорость которого пропорциональна радиусу. Кинематической характеристикой вихревого течения жидкости является циркуляция скорости, которая служит мерой завихренности. '
где: Г - циркуляция вектора скорости, - проекция вектора скорости на касательную к этому контуру в i-той точ- ке
В тех случаях, когда вращение жидкости в определённых точках пространства происходит с постоянной скоростью и положение вихря с течением времени не меняется, то такое вихревое движение принято называть стационарным вихрем В иных случаях вихревое движение следует считать не стационарным. Поток жидкости Поток жидкости представляет собой совокупность элементарных струек жидкости. По этой причине основные кинематические характеристики потока во многом совпадают по своему смыслу с аналогичными характеристиками для элементарной струйки жидкости. Тем не менее, различия всё же имеются. Так в отличие от элементарной струйки, которая отделена от остальной жидкости поверхностью трубки тока, образованной линиями тока, поток жидкости имеет реальные границы в виде твёрдой среды, газообразной или жидкой сред. По типу границ потоки можно разделить на следующие виды: напорные, когда поток ограничен твёрдой средой по всему периметру сечения, безнапорные, когда часть сечения потока представляет собой свободную поверхность жидкости, гидравлические струи, когда поток ограничен только жидкой или газообразной средой. Если гидравлическая струя ограничена со всех сторон жидкостью, то она называется затопленной гидравлической струёй, если гидравлическая струя ограничена со всех сторон газовой средой, то такая струя называется незатопленной. Поперечное сечение потока, расположенное нормально к линиям тока, называется живым сечением потока. Площадь живого сечения потока определяется соотношением:
Расход жидкости в потоке определяется как отношение объёма жидкости протекающее через живое сечение потока к интервалу времени или определяется следующим соотношением:
Кроме известной размерности расхода в системе СИ м3/с имеется целый набор внесистемных единиц для измерения расхода жидкости в потоке: м3/сут, л/чс, л/с, и др. Средней скоростью в живом сечении потока называется величина:
Смоченным периметром живого сечения потока П называется часть контура живого сечения потока, которая ограничена твёрдой средой. (На рисунке смоченный пери Отношение площади живого сечения потока к длине смоченного периметра называется гидравлическим радиусом живого сечения.
Величина гидравлического радиуса круглого сечения радиуса г:
равна половине величины его геометрического радиуса. Величина гидравлического радиуса трубы квадратного сечения со стороной а, (полностью заполненной жидкостью) равна Динамика идеальной жидкости 4.1. Дифференциальное уравнение движения идеальной жидкости (при установившемся движении) и его интегрирование Для вывода уравнения движения жидкости обратимся к записанному ранее уравнению равновесия жидкости (в проекциях на координатные оси), иначе говоря:
Тогда уравнение движения жидкости в проекциях на координатные оси можно записать в следующем виде:
Согласно основному положению о поле скоростей (метод Эйлера) для проекций скоростей движения жидкости можно записать следующее:
или (для установившегося движения жидкости):
Найдём первые производные от скоростей по времени, т.е. определим ускорения вдоль осей координат:
отметим, что:
' * / Теперь подставив выражения для ускорений в исходную систему дифференциальных уравнений движения жидкости, получим систему уравнений Эйлера в окончательном ви-де2:
Теперь вновь обратимся к системе дифференциальных уравнений движения жидкости, умножив обе части 1-го уравнения на dx, 2-го уравнения на dy, 3-го уравнения на dz, получим:
и просуммировав эти уравнения по частям, получим:
2 При неустановившемся движении жидкости уравнения Эйлера дополняются первыми слагаемыми.
Преобразуем левую часть полученного уравнения, полагая, что
Слагаемые в правой части уравнения являются полными дифференциалами функций.
Теперь уравнение примет вид
Если из массовых сил на жидкость действует только сила тяжести, то >,* тогда получим:
После интегрирования получим:
разделив почленно все члены уравнения на g, получим так называемое уравнение Бернулли
Здесь величина Н называется гидродинамическим напором Величина гидродинамического напора постоянна для всех живых сечений элементарной струйки идеальной жидкости.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.005 с.) |

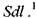
 Масса жидкости, вошедшая в элементарную трубку тока за временной интервал dt, будет равна:
Масса жидкости, вошедшая в элементарную трубку тока за временной интервал dt, будет равна: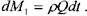
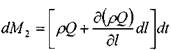
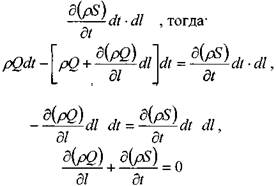 *
*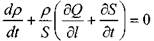
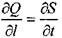
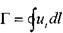 5
5 - элемент длины контура
- элемент длины контура


 метр выделен жирной линией).
метр выделен жирной линией).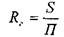


 . Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодействующая отлична от 0,
. Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодействующая отлична от 0,  то жидкость начнёт двигаться с некоторой скоростью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, составляющие жидкое тело получат ускорение.
то жидкость начнёт двигаться с некоторой скоростью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, составляющие жидкое тело получат ускорение.




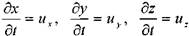





 в результате запишем
в результате запишем


 , и
, и
 ?
?



