
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация сил, действующих в жидкостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Классификация сил, действующих в жидкости По характеру действия силы можно разделить на две категории: массовые силы и поверхностные. Массовые силы. Силы, действующие на каждую частицу жидкости с массой D М = rD V, то есть силы, распределенные по массе, называются массовыми. К ним относятся: сила тяжести, силы инерции, гравитационные силы, подчиняющиеся закону всемирного тяготения Ньютона. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой Δ M = ρ V действует сила Δ F, в зависимости от ее массы. Пусть объем Δ V содержит в себе точку А. Тогда в точке А: Если по аналогии определить плотность этих сил, то: нормальное напряжение в точке А: Поверхности равного давления. Поверхность, все точки которой испытывают одинаковое давление, называются поверхностью равного давления. Анализируя основное уравнение гидростатики можно заключить, что поверхностями равного давления в объеме покоящейся относительно земли жидкости являются горизонтальные плоскости (при p = const будет и z = const) Свободной поверхностью называют поверхность жидкости, которая граничит с газовой средой. Все точки такой поверхности испытывают одинаковое внешнее давление p0. Свободная поверхность представляет собой поверхность равного давления и она горизонтальна, если на жидкость действуют только силы тяжести (рис. 1).
В случае покоя жидкости относительно сосуда, который движется с ускорением а, на частицы жидкости действуют силы тяжести и силы инерции в противоположную сторону движения (рис.2). При равновесии равнодействующая должна быть перпендикулярна свободной поверхности, которая является поверхностью равного давления. В рассматриваемом случае свободная поверхность наклонена к горизонту под углом α (tgα = a/g). При относительном покое жидкости в сосуде, который вращается с угловой скоростью ω, на каждую частицу с координатой r действуют силы тяжести, равные gm, и центробежные силы инерции, равные mω2r.
1 2 ДАВЛЕНИЕ ЖИДКОСТИ НА ЦИЛИНДРИЧЕСКИЕ СТЕНКИ Рассмотрим некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой. Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости, которое сводится к тому, что в каждой точке на стенку действует давление жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими и выразим элементарную силу давления на них в общем виде dP = pd w. Силы dP уже не будут направлены параллельно друг другу, их линии действия могут не пересекаться в одной точке, и их сумма может не сводиться к одной равнодействующей. Для шаровой или круговой цилиндрической стенки элементарные силы давления направлены по радиусам, пересекутся в центре сферы или в центре круга. ЗАКОН АРХИМЕДА Рассмотрим полностью погруженное в жидкость твердое тело, объем которого Wт, а форма такова, что любая прямая пересекает поверхность этого тела только в двух точках (рис. 3.21). Для определения силы Р давления жидкости на тело воспользуемся результатами предыдущего пункта. Горизонтальные составляющие силы Рх и Ру взаимно уравновешиваются. Вертикальная составляющая силы давления Рz равна весу жидкости в объеме тела. Действительно, в данном случае имеем два тела давления: ABMNAEF, соответствующее давлению на верхнюю часть тела, и
Вертикальная составляющая Равнодействующая сила давления равна разности указанных составляющих:
или
Силу Pz называют архимедовой силой. Так как Рх = Ру = 0, то Р = Рz.
Виды движения жидкости Равномерное движение характеризуется параллельностью и прямолинейностью линий тока. Размеры и форма живых сечений и средние скорости потока по его длине не изменяются. Местные скорости в соответственных точках всех живых сечений по длине потока одинаковы. Ускорения при равномерном движ = нулю. В безнапорном равномерном потоке как следствие вышесказанного и глубины будут неизменными по длине. Неравномерное движ - семейство линий тока не представлено параллельными прямыми. Площади живых сечений и средние скорости могут быть переменными по длине потока. Неравномерное движ может быть ускоренным или замедленным.Среди неравномерных движ выделяют плавно изменяющееся движ, которое характеризуется: линии тока примерно параллельны, кривизна их достаточна мала; живые сечения можно считать плоскими; изменения формы и площади живых сечений по длине потока происходят весьма плавно. В связи с отмеченными особенностями при расчетах плавно изменяющихся потоков пренебрегают составляющими скоростей в плоскости живого сечения. Неустановившееся (нестационарное) движение по характеру изменения скоростей во времени подразделяется на быстро изменяющееся и медленно изменяющееся. В движущейся жидкости различают продольную и поперечные составляющие скорости. Обычно направление оси ОХ совпадает с направлением продольной скорости. Направление поперечных составляющих скорости совпадает с направлениями осей OY и OZ. Распределение продольных скоростей по живому сечению или в различных точках вертикали, принадлежащей данному живому сечению, характеризует эпюра скоростей. Для всех точек живого сечения эпюра скоростей—объемная фигура, а эпюра скоростей на данной вертикали — плоская фигура. Движения также подразделяются на пространственные, плоские и одномерные. Плоским (двухмерным) движением считается такое, при котором кинематические характеристики зависят только от двух координат н не зависят от третьей. Одномерным движением называется такое, в котором скорости зависят только от одной координаты. Классификация потоков по характеру границ. Потоком жидкости в гидравлике называют движущуюся массу жидкости, ограниченную направляющими твердыми поверхностями, поверхностями раздела жидкостей или свободными поверхностями. В зависимости от характера и сочетания ограничивающих поток поверхностей потоки делятся на безнапорные, напорные потоки и гидравлические струи. Классификация потерь напора Потери удельной энергии, затрачиваемой на преодоление сопротивлений движению вязкой жидкости двух видов:1) потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков трубы, по которым движется жидкость, – потерь по длине hдл; 2) потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам труб – местных потерь напора hм. Общие потери напора в системе труб равны сумме потерь напора по длине отдельных участков и всех местных потерь напора:
3) неравномерное плавно изменяющееся движение: ламинарное и турбулентное; 4) неравномерное движение с изменением средней скорости и эпюры скоростей в пределах коротких участков, называемых местными сопротивлениями: ламинарное и турбулентное. Различие кинематической структуры для каждого из перечисленных видов движения определяет различие в расчетных зависимостях для потерь напора по длине.
29. Касательные напряжения и их распределение при равномерном движении. Рассмотрим равномерное напорное движение жидкости в прямолинейной наклонной трубе, рис. 7.5, радиусом r 0 с площадью живого сечения w и смоченным периметром c. Выделим отсек длиной l и составим уравнение равномерного движения массы жидкости, заключенной в отсеке. При равномерном движении сумма проекций на направление движения (на ось трубы) внешних сил, действующих на жидкость в выделенном отсеке, должна быть равна нулю:
где Р – равнодействующая сила давления в сечениях 1 - 1 и 2-2; Т – направленная против течения равнодействующая сил трения, действующих на боковой поверхность отсека c l; G – вес жидкости в выделенном отсеке. Тогда:
где t0 – касательное напряжение на стенке трубы; р 1 и р 2 – давления, действующие в центрах тяжести торцевых сечений отсека w1 = w2 = w; z 1 и z 2 – координаты центров тяжести этих сечений. Учитывая, что
Разделив все члены уравнения на rgw, получим:
При равномерном движении:
Тогда касательные напряжения на стенке трубы:
Так как w / c = R – гидравлический радиус, а hдл / l = J – гидравлический уклон, то:
или
Распределение касательных напряжений по сечению трубы может быть выяснено следующим образом. Выделим в потоке цилиндрический отсек жидкости, боковая поверхность которого отстоит от оси трубы на размер r, меньший чем радиус трубы r 0. Тогда для трубы получим:
где t – касательное напряжение, действующее на боковой поверхности выделенного в жидкости цилиндра с радиусом поперечного сечения r. Сравнивая (7.3) и (7.4), видим, что:
Так как r = r 0 – z', где z ' – расстояние по нормали от стенки трубы до рассматриваемой боковой поверхности отсека, то имеем:
Следовательно, при равномерном движении касательное напряжение по радиусу трубы распределено по линейному закону. Согласно (7.5) касательное напряжение на стенке (при z ' = 0) имеет максимальное значение, равное t0. На оси трубы касательное напряжение равно нулю. Приведем другую формулу для hдл:
Таким образом, видно что при равномерном движении потери напора по длине в данных условиях (l, r, g, R) можно определять через касательное напряжение на стенке. Классификация сил, действующих в жидкости По характеру действия силы можно разделить на две категории: массовые силы и поверхностные. Массовые силы. Силы, действующие на каждую частицу жидкости с массой D М = rD V, то есть силы, распределенные по массе, называются массовыми. К ним относятся: сила тяжести, силы инерции, гравитационные силы, подчиняющиеся закону всемирного тяготения Ньютона. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой Δ M = ρ V действует сила Δ F, в зависимости от ее массы. Пусть объем Δ V содержит в себе точку А. Тогда в точке А: Если по аналогии определить плотность этих сил, то: нормальное напряжение в точке А:
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.195 (0.012 с.) |

 , где FА – плотность силы в элементарном объеме. Плотность массовой силы – векторная величина, отнесена к единичному объему Δ V; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. Т.е плотность массовой силы ведет себя, как массовая сила. Поверхностные силы. Силы, действующие на каждый элемент Dw поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называются поверхностными. Поверхностные силы делятся на две группы: нормальные и касательные. К нормальным поверхностным силам относится сила давления D Р, к касательным относится сила трения D Т.
, где FА – плотность силы в элементарном объеме. Плотность массовой силы – векторная величина, отнесена к единичному объему Δ V; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. Т.е плотность массовой силы ведет себя, как массовая сила. Поверхностные силы. Силы, действующие на каждый элемент Dw поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называются поверхностными. Поверхностные силы делятся на две группы: нормальные и касательные. К нормальным поверхностным силам относится сила давления D Р, к касательным относится сила трения D Т. , касательное напряжение в точке А:
, касательное напряжение в точке А:  . И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.
. И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.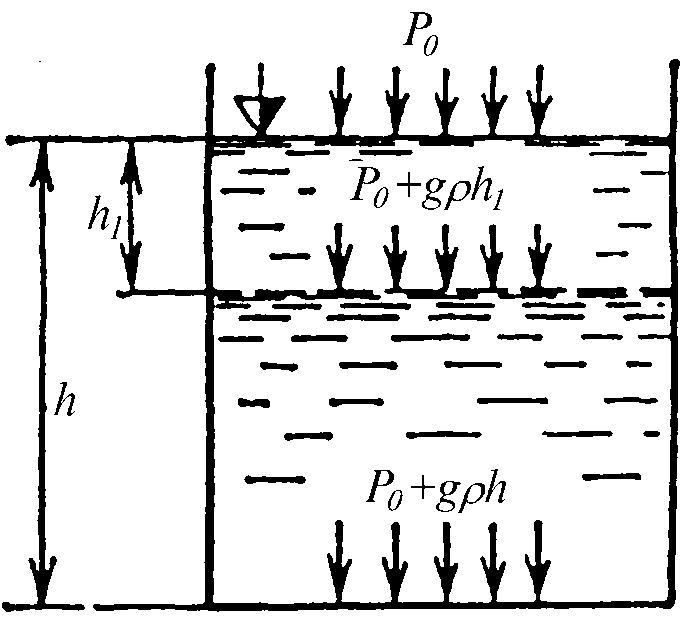
 В этом случае поверхность равного давления представляет собой параболлоид вращения.
В этом случае поверхность равного давления представляет собой параболлоид вращения. , равна весу жидкости в объеме W 1, то есть rg W 1, и направлена по вертикали вниз. Вертикальная составляющая
, равна весу жидкости в объеме W 1, то есть rg W 1, и направлена по вертикали вниз. Вертикальная составляющая  , равна весу жидкости в объеме W 2, то есть r gW 2, и направлена по вертикали вверх.
, равна весу жидкости в объеме W 2, то есть r gW 2, и направлена по вертикали вверх.

 . Эти потери энергии обусловлены переходом механической энергии потока в тепловую. Процесс этот необратим. Наличие гидравлических сопротивлений при движении вязкой жидкости связано с работой сил трения внутри жидкости. Благодаря силам трения механическая энергия может перейти в теплоту. Классификация движений по характеру поля скоростей (установившиеся движение): 1) равномерное движение с постоянными по длине средней скоростью и эпюрой скоростей: ламинарное и турбулентное; 2) неравномерное движение с постоянной по длине средней скоростью и изменяющейся по длине эпюрой скоростей: ламинарное и турбулентное;
. Эти потери энергии обусловлены переходом механической энергии потока в тепловую. Процесс этот необратим. Наличие гидравлических сопротивлений при движении вязкой жидкости связано с работой сил трения внутри жидкости. Благодаря силам трения механическая энергия может перейти в теплоту. Классификация движений по характеру поля скоростей (установившиеся движение): 1) равномерное движение с постоянными по длине средней скоростью и эпюрой скоростей: ламинарное и турбулентное; 2) неравномерное движение с постоянной по длине средней скоростью и изменяющейся по длине эпюрой скоростей: ламинарное и турбулентное; ,
, ,
, , имеем:
, имеем: .
. .
. .
. .
. ,
, . (7.3)
. (7.3) , (7.4)
, (7.4) .
. . (7.5)
. (7.5) .
.


